
Киселева Г.А. Математика часть 2
.pdf
|
ln x = |
|
|
|
ln x |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. lim |
= lim |
= lim |
|
x |
|
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x |
x |
x |
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln x |
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
|
|
ln x |
|
|
|
|
|
x |
|
|
|||||||||||
3. lim |
xln x = 0 = lim |
|
|
= |
= |
lim |
|
|
|
|
= |
lim |
|
|
|
|
|
|
= |
||||||
|
|
1 |
|
|
|
1 |
|
||||||||||||||||||
x 0 |
|
|
|
x 0 1 |
|
|
|
x 0 |
|
|
x 0 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
||
= lim x |
= 0. |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. lim |
|
1 |
tg x |
|
= [ - ] = lim |
1 sin x = |
0 |
= |
|||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
|
|||||||
|
x 2 cos x |
|
|
|
|
|
|
|
|
x 2 |
|
0 |
|
||||||||
= lim |
cos x |
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
(x |
2 |
|
|
5. |
lim x2e x = |
|
0 |
|
= |
lim |
|
|
= |
= lim |
|
) |
|||||||||
e |
x |
|
|
|
|
(e |
x |
|
|||||||||||||
|
x |
|
|
|
|
|
x |
|
|
x |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
||||
lim |
1 sin x |
= |
|
|
|
x 2 |
cos x |
|
= lim 2x =
x ex
= |
|
= lim |
(2x) |
= lim |
2 |
= 0. |
|
|
|
|
|
||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||||
|
|
x |
(e |
) |
|
|
x |
e |
x |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
6. |
lim xx = [0 0] = lim ex ln x = [в силу непрерывности e x] = |
|||||||||||||||||||
|
|
|
x 0 |
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
||
|
lim |
x ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ex 0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
x ln x |
|||
|
Так как lim xln x 0 |
|
|
|
|
|
|||||||||||||||
|
(см. пример 3), то ex 0 |
e0 1. |
|||||||||||||||||||
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
2 |
|
|
|
7. lim 1 x |
2 |
|
|
= [1 |
|
lim e |
ex 1 x ln 1 x |
|
= [в силу непре- |
|||||||||||
|
ex 1 x |
||||||||||||||||||||
|
|
|
|
|
|
] = |
|
|
|
||||||||||||
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
lim |
ln 1 x2 |
|
|
|
|
|
|
|
||||
рывности e x] |
|
|
|
|
|
ex 1 x |
|
. Так как |
|
|
|
||||||||||
= ex 0 |
|
|
|
|
|||||||||||||||||
11
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
ln 1 x2 |
|
0 |
|
|
|
ln 1 x2 |
|
|
|
|
|
|
|
||||||||||
lim |
= |
= lim |
= |
lim |
1 x 2 |
= |
|||||||||||||||||||
|
ex 1 x |
|
0 |
ex 1 x |
|
ex 1 |
|||||||||||||||||||
x 0 |
|
|
|
x |
0 |
|
x 0 |
|
|
||||||||||||||||
|
|
|
|
2 x |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
= |
= |
lim |
|
(2 x) |
|
|
|
|
= |
|
|
|||||
ex 1 1 x 2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x 0 |
|
|
|
x 0 ex 1 1 x 2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
lim |
ln 1 x2 |
|
|
|
|
|
||||
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
ex 1 x |
|
= e 2. |
|
||||||||
|
|
|
|
|
|
|
|
|
|
= 2, то |
ex 0 |
|
|
||||||||||||
|
|
x |
|
2 |
|
|
|
x |
|
|
|
|
|||||||||||||
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
e |
1 x |
|
e |
1 2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
8. lim tg
x
2
x 2 cos x = [ 0] = lim e 2 cos x ln tg x = [в силу непрерывно- |
|
x |
|
|
2 |
|
|
|
|
2 lim |
ln tg x |
|
|
|
|
|
ln tg x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
π |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
сти e x] = е |
x |
|
|
|
|
cos x . Так как |
lim |
|
|
|
|
= |
|
= |
lim |
|
ln tg x |
|
= |
||||||||||||||||||
2 |
|
|
|
1 |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
cos x |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 lim |
ln tg x |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
tg x |
|
|
cos2 x |
|
|
cos x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= lim |
|
|
|
|
|
|
= |
lim |
= 0, то |
еx 2 |
|
cos x |
|
|
|
= e 0 = 1. |
|||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
x |
|
|
|
|
|
|
|
|
sin x |
x |
sin2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
cos |
2 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2.2. Возрастание и убывание функций
Функция y (x) возрастает (убывает) на некотором промежутке тогда и только тогда, когда для любых x 1, x 2 из этого промежутка из неравенства x 1 < x 2 следует неравенство y (x 1) < y (x 2)
((y (x 1) > y (x 2)).
Теорема 1 (необходимое условие монотонности). Если диффе-
ренцируемая на некотором промежутке функция возрастает (убы-
12
вает) на нем, то на этом промежутке производная функции больше нуля (меньше нуля).
Теорема 2 (достаточное условие монотонности). Если на не-
котором промежутке существует положительная (отрицательная) производная функции, то на этом промежутке функция возрастает (убывает).
Пример 1. Исследовать на монотонность функцию y = x 2.
1)Область определения функции: R.
2)y = 2 x.
y > 0 при x > 0. Следовательно, функция y = x 2 возраста-
ет на (0; + ).
y < 0 при x < 0. Следовательно, функция y = x 2 убывает на (- ; 0).
2.3. Экстремум функции
Точка x 0 называется точкой локального максимума (миниму-
ма) функции y (x), если существует такая окрестность точки x 0, что для всех x из этой окрестности, за исключением самой точки
x 0, выполняется y (x ) < y (x 0) (y (x) > y (x 0)). При этом y (x 0) назы-
вают максимумом (минимумом) функции y (x).
Теорема 3 (необходимое условие экстремума). Ели функция дифференцируема в некоторой точке и имеет в ней экстремум, то производная функции в этой точке равна нулю.
Замечание. Функция может иметь экстремум и в точках, в которых она не дифференцируема. Поэтому точки, в которых функция может иметь экстремум, ищут среди тех точек, где производная равна нулю или не существует. Их называют критическими точками.
Теорема 4 (первое достаточное условие экстремума). Пусть функция y = y (x) дифференцируема в некоторой окрестности точки x 0 (кроме, быть может, самой точки x 0). Если x 0 критическая точка функции и если производная функции при переходе через точку x 0 (слева направо) меняет знак с «+» на «-», то x 0 –
13

точка максимума функции; если она меняет знак с «-» на «+», то x 0 – точка минимума функции.
Теорема 5 (второе достаточное условие экстремума). Если x 0 – критическая точка функции и если вторая производная функции в точке x 0 положительна, то x 0 – точка минимума функции; если вторая производная отрицательна, то x 0 – точка максимума функции.
Пример 2. Исследовать на экстремум функцию y = x 3 –
–3x + 2.
1)Область определения функции: R.
2)y = (x 3 – 3x + 2) = 3x 2 – 3;
y = 0 при 3x 2 – 3 = 0 или x = 1; y существует для любого x. Следовательно, x = 1, x = –1 – критические точки.
3) I способ. Используем теорему 4:
у' (х) + |
|
– |
+ |
y(x) |
–1 |
1 |
x |
|
|
|
|
|
max |
min |
|
Следовательно, x = –1 – точка максимума, x = 1 – точка минимума.
II способ. Используем теорему 5: y = (3x 2 – 3) = 6x;
y (1) = 6 1 = 6 > 0 x = 1 – точка минимума;
y (–1) = 6 (–1) = –6 < 0 x = –1 – точка максимума.
2.4. Наибольшее и наименьшее значение функции на от-
резке
Пусть функция непрерывна на отрезке. Тогда по свойствам непрерывных функций она достигает на нем своего наибольшего и наименьшего значений.
14
Для нахождения наибольшего и наименьшего значений функции непрерывной на отрезке необходимо:
а) найти критические точки функции; б) найти значения функции на концах отрезка и в критических
точках, принадлежащих отрезку; в) выбрать наибольшее и наименьшее.
Пример 3. Найти наибольшее и наименьшее значение функ-
ции y = x 3 – 3x + 2 на [–2; 0].
1)x = 1, x = –1 – критические точки данной функции (см. пример 2).
2)y (–2) = (–2) 3 – 3 (–2) + 2 = 0 – наименьшее; y (0) = 0 3 – 3 0 + 2 = 2;
y (–1) = (–1) 3 – 3 (–1) + 2 = 4 – наибольшее.
Ответ: min |
x3 3x 2 0 , |
max x3 3x 2 4. |
[ 2; 0] |
|
[ 2; 0] |
|
|
2.5. Выпуклость функции. Точки перегиба
График функции называется выпуклым вверх (выпуклым вниз)
на некотором промежутке, если на этом промежутке график функции расположен ниже (выше) любой касательной, проведенной к нему.
Теорема 6 (достаточное условие выпуклости). Если функция на некотором промежутке имеет положительную (отрицательную) вторую производную, то график функции на этом промежутке выпуклый вниз (выпуклый вверх).
Точка графика функции, при переходе через которую график функции меняет направление выпуклости, называется точкой перегиба графика функции.
Теорема 7 (необходимое условие перегиба). Если в некоторой точке график дважды дифференцируемой функции имеет перегиб, то вторая производная функции в этой точке равна нулю.
Теорема 8 (достаточное условие перегиба). Если вторая про-
изводная функции y (x) в точке x 0 равна нулю или не существует и если при переходе через точку x 0 вторая производная меняет знак, то точка (x 0, y (x 0)) – точка перегиба графика функции y (x).
15
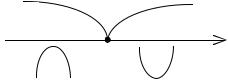
Пример 4. Исследовать на направление выпуклости и точки перегиба функцию y = x 3 – 3x + 2.
1)Область определения функции: R.
2)y = (x 3 – 3x + 2) = 3x 2 – 3.
3)y = (3x 2 – 3) = 6x;
y = 0 при x = 0;
y существует для любого x. Используем теорему 8:
y |
– |
+ |
y |
0 |
x |
Найдем значение функции в точке х = 0:
y (0) = 0 3 – 3 0 + 2 = 2.
Итак, график функции y = x 3 – 3x + 2 |
выпуклый |
вверх на |
промежутке (– ; 0); выпуклый вниз на |
промежутке |
(0; + ); |
(0; 2) – точка перегиба графика функции. |
|
|
2.6. Асимптоты графика функции
Асимптота кривой – это прямая, к которой кривая приближается сколь угодно близко при удалении в бесконечность.
|
Вертикальная асимптота |
|
Если lim |
y x или |
lim y x , то график функции |
x a |
|
x a |
y = y (x) имеет вертикальную асимптоту x = a.
Для функции y (x) точка a – точка разрыва второго рода.
16
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Наклонная асимптота |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Если |
существуют |
конечные |
пределы |
lim |
|
y x |
k |
|
|
|
и |
|
||||||||||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
x k x] b, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
lim |
[ y |
|
|
|
то график функции y = y (x) |
|
имеет наклон- |
|
||||||||||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ную асимптоту y = k x + b. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Если |
|
|
|
|
lim |
|
y x |
0 |
и |
|
|
существует |
конечный |
|
предел |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
lim |
y x b , то график функции y = y (x) имеет горизонтальную |
|
||||||||||||||||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
асимптоту |
|
y = b. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 5. Найти асимптоты графика функции |
y |
|
x2 |
2x 3 |
. |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
Область определения функции: R\{0}. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
2) |
lim y x lim |
|
|
|
x2 |
2x 3 |
; lim y x lim |
|
x2 |
2x 3 |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
||||||||||||||||||||||||||||
|
x 0 |
|
|
|
x 0 |
|
|
|
x |
|
|
|
|
|
x 0 |
|
x 0 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
. Следовательно, |
x = 0 – вертикальная асимптота. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
k |
|
|
|
|
x2 2x 3 |
|
|
|
|
|
|
x2 2x 3 |
|
|
|
|
|
|
2x 2 |
|
|
|
|
|
|
||||||||||||||||||
3) |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
= |
|
lim |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
2x |
|
|
|
|
|||||||||||||||||||||
|
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
lim 2x |
2 |
= lim |
1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
(2x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
x2 |
2x 3 |
|
|
|
|
|
|
|
|
x2 2х 3 x2 |
|
|
|
|
2x 3 |
|
|
|
|
|
|||||||||||||||||||||
b lim |
|
|
|
|
|
|
|
|
|
|
|
|
x |
= |
lim |
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
= |
|||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= lim (2x 3) |
lim |
2 |
|
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
x |
|
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Следовательно, y = x + 2 – наклонная асимптота.
17

Решение примерного варианта контрольной работы
Задача 1. Найти предел функции, используя правило Лопита-
ля:
|
|
1 |
|
lim x e x |
1 . |
||
x |
|
|
|
|
|
|
|
Решение
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
ex 1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
x |
1 |
|
|
|
|
|
|
|
|
|||||
|
lim x e x |
1 |
= [ 0] = |
|
lim |
|
= |
= lim |
|
|
|
= |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
x 1 |
|
x |
1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
1 |
1 |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
ex |
|
|
|
|
ex |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
= |
lim |
|
|
x |
|
= |
lim |
|
|
|
|
= |
lim ex |
1. |
|
|
|
|
|
|||||||||
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
x |
|
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
x2 |
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: 1.
Задача 2. Найти интервалы монотонности и экстремумы функ-
ции y = (x – 2) 2.
Решение
1)Область определения функции: R.
2)y = ((x – 2) 2) = 2 (x – 2) (x – 2) = 2 (x – 2);
y = 0 при x – 2 = 0 или x = 2; y существует для любого x. Следовательно, x = 2 – критическая точка.
3)Используем теорему 4:
y |
|
– |
+ |
|
y |
2 |
x |
|
||
18 |
min |
|
|
|

Найдем значение функции в точке минимума:
y (2) = (2 – 2) 2 = 0.
Ответ: график функции убывает на промежутке (– ; 2); возрастает на промежутке (2; + ); x = 2 – точка минимума функции; 0 – минимум функции.
1
Задача 3. Найти асимптоты графика функции y e3 x .
Решение
1) Так как 3 – x = 0 при x = 3, то область определения функ-
ции: R\{3}.
|
1 |
|
|
1 |
|
||
2) lim y x lim e |
|
, |
lim y x lim e |
|
0 . |
||
3 x |
3 x |
||||||
x 3 |
x 3 |
x 3 |
x 3 |
||||
Следовательно, x = 3 – вертикальная асимптота.
|
y x |
|
1 |
|
|
1 |
|
||
|
lim e3 x |
|
|
|
|||||
|
|
b lim y x = lim e |
|
1. |
|||||
3) k lim |
0 , |
3 x |
|||||||
x |
|||||||||
x |
x |
x |
|
x |
x |
||||
Следовательно, y = 1 – горизонтальная асимптота.
1
Ответ: график функции y e3 x имеет вертикальную асимптоту x = 3 и горизонтальную асимптоту y = 1.
Задача 4. Найти интервалы выпуклости и точки перегиба гра-
фика функции |
y |
1 |
. |
||
x2 9 |
|||||
|
|
|
|
||
Решение |
|
|
|
|
|
1) Так как |
x |
2 – 9 = 0 при x = 3, то область определения |
|||
функции: R\{–3; |
3}. |
|
|||
19
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2) |
y |
|
|
|
|
|
|
|
|
= |
|
|
|
|
x2 |
|
9 = |
|
|
|
|
. |
|
|
|
|
||||||||||
|
|
|
2 |
9 |
x2 |
9 |
2 |
x2 9 |
2 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
2x |
|
|
|
|
|
|
|
x |
9 |
|
|
x x |
9 |
|
|
|
|
||||||||||
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||||||||||||||||
|
3) |
|
|
x |
2 |
9 |
2 |
|
= 2 |
|
|
|
x |
2 |
9 |
4 |
|
|
|
|
|
|
= |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= 2 |
x2 9 2 |
x 2 x2 9 x2 9 |
= 2 |
x2 9 2x 2x |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x2 9 4 |
|
|
|
|
|
|
x2 9 3 |
|
|
|
||||||||||||||||
|
6 x2 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x2 |
9 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
y ≠ 0, |
так как |
6 (x 2 + 3) ≠ 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
y не существует при (x 2 – 9) 3 = 0, |
|
или x = 3. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
4) |
Используем теорему 8: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
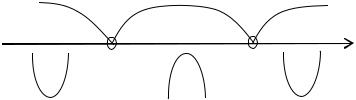
y |
+ |
– |
+ |
y |
–3 |
3 |
x |
Точки x = 3 не принадлежат области определения функции, следовательно, точек перегиба нет.
Ответ: график функции |
y |
|
1 |
выпуклый вверх на про- |
|
x2 9 |
|||||
|
|
|
|||
межутке (–3; 3) и выпуклый |
вниз |
на |
промежутке (– ; –3) |
||
(3; + ); точек перегиба нет. |
|
|
|
|
|
Задача 5. Найти наибольшее и наименьшее значение функции y = 9x 4 + 4x 3 – 7 на [–1; 2].
20
