УП Информатика

Для представления функции алгебры логики в форме (1) используется совокупность термов, объединенных знаками дизъюнкции

( или +).

Можно использовать также другую элементарную логическую

где k – количество двоичных наборов, для которых Ф = 0.

Нормальная конъюнктивная форма (НКФ) – объединение тер-

мов (2), включающее в себя дизъюнктивные термы разных рангов

[1].

2.5. Совершенные нормальные формы

Нормальные конъюнктивная, дизъюнктивная формы не дают однозначного представления о функции. Такое представление получается только при совершенных нормальных формах (СНФ).

В общем виде переменная может быть задана как некоторая функция

x, если α = 1; xα =

x , если α = 0,

тогда функция алгебры логики может быть представлена в виде

Совершенная нормальная дизъюнктивная форма (СНДФ) –

ФАЛ, заданная в виде (3). Это булева функция, представленная в

41

виде дизъюнкции элементарных конъюнкций, ранг которых равен числу независимых переменных n.

Основные свойства СНДФ:

вСНДФ нет двух одинаковых конъюнктивных термов;

вСНДФ ни один конъюнктивный терм не содержит двух одинаковых множителей (переменных);

вСНДФ ни один конъюнктивный терм не содержит вместе с переменной и ее отрицание.

На основании этих свойств получение СНДФ из таблицы истинности производится по правилу:

1) из таблицы истинности выбираются все наборы значений ар-

гументов x1, x2, … , xn, на которых функция равна 1;

2) для каждого из таких наборов составляются конъюнкции из n переменных (причем переменная входит в конъюнкцию с отрицанием, если ее значение на этом наборе равно 0, и без отрицания, если ее значение равно 1);

3) полученные конъюнкции соединяются знаками дизъюнкции.

П р и м е р . Представить функцию, заданную табл. 6, в СНДФ.

Р е ш е н и е . Решение проводится в соответствии с вышеприведенным правилом.

Ответ: f (x1, x2 , x3 ) = x1x2 x3 + x1x2 x3 + x1x2 x3 .

Любая ФАЛ, кроме абсолютно истинной функции, может

быть представлена в совершенной конъюнктивной нормальной форме (СКНФ):

42

f(x1, x2 , ..., xn ) =

=(x1 x2 x3 )(x1 x2 x3 )(x1 x2 x3 )(x1 x2 x3 )(x1 x2 x3 ).

Представление этой функции по формуле (4) более громоздкое, чем ее представление в СНДФ, так как в табл. 6 много строк, для которых f = 0.

Базис И, ИЛИ, HЕ является избыточной системой. Возможно удаление из него некоторых функций. Например, используя законы де Моргана, можно удалить либо функцию И, заменив ее на функции ИЛИ и НЕ, либо функцию ИЛИ, заменив ее на функции И и НЕ.

С одной стороны, если сравнить в смысле минимальности различные формы представлений ФАЛ, то станет ясно, что нормальные формы экономичнее совершенных нормальных форм. С другой стороны, нормальные формы не дают однозначного представления.

Минимальная форма представления ФАЛ – форма представле-

ния ФАЛ, которая содержит минимальное количество термов и переменных в термах (т. е. минимальная форма не допускает никаких упрощений) [1].

П р и м е р . Функция f ( x1, x2 , ..., xn ) = x1 + x2 является минимальной формой, и, наоборот, функция x1 + x1 x2 может быть упрощена, если к этому выражению применить распределительный закон, т.е.

x1 + x1x2 = (x1 + x1)(x1 + x2 ) = x1 + x2.

Контрольные вопросы

1. Дайте определения основных понятий алгебры логики.

43

2.Назовите и определите основные логические функции.

3.Назовите и поясните свойства элементарных функций алгебры логики.

4.Какие способы задания логических функций вам известны?

5.Что такое функционально полный набор логических функций?

6.Назовите основные законы алгебры логики и приведите примеры их использования.

Задания для самостоятельного решения

1. Записать в аналитическом виде функцию, заданную в табл. 7.

2.Для функции, заданной в табл. 7, построить нормальную дизъюнктивную форму.

3.Для функции, заданной в табл. 7, построить нормальную конъюнктивную форму.

4.Для функции, заданной в табл. 7, построить совершенную дизъюнктивную нормальную форму.

5.Для функции, заданной в табл. 7, построить совершенную нормальную конъюнктивную форму.

6.Построить таблицу истинности для следующих функций:

а) f(х1, х2, х3) = x1+ ¬ х2 х3+¬ х1 х2 х3 + х1¬ х3;

б) f(х1, х2, х3) = x1+ х2;

в) f(х1, х2, х3) = x1+¬ (х2 х3).

44

7.Найти СДНФ и СКНФ для функций, определенных в задании 6.

8.Доказать практически справедливость законов де Моргана, поглощения и склеивания.

9.Доказать, что свойство ассоциативности несправедливо для функции импликации.

3.МЕТОДЫ ЭФФЕКТИВНОГО И ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ ИНФОРМАЦИИ

3.1. Основные понятия теории кодирования

Задача кодирования информации представляется как некоторое преобразование числовых данных в заданной системе счисления. В частном случае эта операция может быть сведена к группированию символов (представление в виде триад или тетрад) или представлению в виде символов (цифр) позиционной системы счисления. Так как любая позиционная система не несет в себе избыточной информации и все кодовые комбинации являются разрешенными, использовать такие системы для контроля правильности работы цифрового автомата не представляется возможным.

Код, содержащий в себе кроме информационных контрольные разряды, называется систематическим кодом.

В контрольные разряды записывается некоторая информация об исходном числе, то есть систематический код обладает избыточностью.

Кодирование на основе систематического кода является помехоустойчивым.

Абсолютная избыточность кода – количество контрольных разрядов k.

Относительная избыточность – отношение k/n, где n = m + k – общее количество разрядов в кодовом слове (m – количество информационных разрядов).

45

Понятие корректирующей способности кода связывается с воз-

можностью обнаружения и исправления ошибки. Количественно корректирующая способность кода определяется вероятностью обнаружения и исправления ошибки.

На практике наиболее часто имеет место вероятность искажения одного символа. Следовательно, основное внимание нужно обратить на обнаружение и исправление одиночной ошибки [1].

Корректирующая способность кода связана также с понятием «кодовое расстояние».

Кодовое расстояние d(A, В) для кодовых комбинаций А и В определяется как вес третьей кодовой комбинации, которая получается поразрядным сложением исходных комбинаций по модулю 2.

Вес кодовой комбинации V(A) – количество единиц, содержащихся в кодовой комбинации.

П р и м е р . Найти вес и кодовое расстояние для комбинаций

А = 011011100, В = 100111001.

9

Р е ш е н и е . Для кодовых комбинаций вес равен V(A) = ∑ ai = 5 ; V(В) =

i=1

9

= ∑ bi = 5 .

i=1

Находим кодовую комбинацию С = A Å B = 111100101, для которой определяется вес, равный кодовому расстоянию для А и В: V (C) = d ( A, B) =

9

= ∑ ci = 6 .

i=1

Ответ: d(A, B) = 6.

В теории кодирования показано, что систематический код способен обнаружить ошибки только тогда, когда минимальное кодовое расстояние для него больше или равно 2t, т. е. dmin ³ 2t , где t – кратность обнаруживаемых ошибок (в случае одиночных ошибок t = 1 и т. д.). Это означает, что между соседними разрешенными кодовыми словами должно существовать по крайней мере одно кодо-

46

вое слово. В тех случаях, когда необходимо не только обнаружить ошибку, но и исправить ее (т. е. указать место ошибки), минимальное кодовое расстояние должно быть dmin ³ 2t +1 [1].

Информационную избыточность можно ввести разными путями. Далее будут рассмотрены методы помехоустойчивого кодирования.

Эффективное кодирование позволяет строить кодовые комбинации с учетом статистических свойств передаваемого сообщения. Основная идея метода эффективного кодирования состоит в том, что буквам, встречающимся часто, присваиваются короткие коды, а буквам, встречающимся редко, присваиваются длинные коды.

В ряде случаев буквы сообщений преобразуются в последовательности двоичных символов. Учитывая статистические свойства источника сообщения, можно минимизировать среднее число двоичных символов, требующихся для выражения одной буквы сообщения, что при отсутствии шума позволит уменьшить время передачи.

Эффективное кодирование базируется на основной теореме Шеннона для каналов без шума. В теореме доказано, что сообщения, составленные из букв некоторого алфавита, можно закодировать так, что среднее число двоичных символов на букву будет сколь угодно близко к энтропии источника этих сообщений, но не меньше этой величины [1].

3.2. Код Шеннона – Фано

Код строится следующим образом:

1)буквы алфавита сообщений выписываются в таблицу в порядке убывания вероятностей;

2)затем они разделяются на две группы так, чтобы суммы вероятностей в каждой из групп были по возможности одинаковы;

3)всем буквам верхней половины в качестве первого символа приписывается 1, а всем нижним – 0;

4)каждая из полученных групп, в свою очередь, разбивается на

47

две подгруппы с одинаковыми суммарными вероятностями и т. д. Процесс повторяется до тех пор, пока в каждой подгруппе не ос-

танется по одной букве.

П р и м е р . Рассмотрим алфавит из восьми букв (табл. 8). При обычном (не учитывающем статистических характеристик) кодировании для представления каждой буквы требуется три символа.

Вычислим энтропию набора букв

8

Н(z) = − ∑ p(zi ) log p(zi ) ≈ 2, 76

i= 1

исреднее число символов на букву

8

lср = ∑ p(zi ) n(zi ) ≈ 2, 84,

i = 1

где n( zi ) – число символов в кодовой комбинации, соответствующей букве zi .

48

Значения Н(z) и lср мало различаются по величине. Условие теоремы Шеннона выполнено: Н(z) <= lср .

Рассмотренная методика Шеннона – Фано не всегда приводит к однозначному построению кода. Ведь при разбиении на подгруппы можно сделать большей по вероятности как верхнюю, так и нижнюю подгруппу.

Множество вероятностей в табл. 8 можно разбить иначе (см. табл. 9). При этом среднее число символов на букву оказывается равным 2,80. Таким образом, построенный код может оказаться не самым лучшим. При построении эффективных кодов с основанием s > 2 неопределенность становится еще больше [1].

3.3. Метод Хаффмена

Метод Хаффмена свободен от недостатка, связанного с неоднозначностью построения кода. Данная методика также использует статистические свойства источника сообщений. Метод гарантирует однозначное построение кода с наименьшим для данного распределения вероятностей средним числом символов на букву.

Для двоичного кода методика сводится к следующему:

1)буквы алфавита сообщений выписываются в основной столбец в порядке убывания вероятностей;

2)две последние буквы объединяются в одну вспомогательную букву, которой приписывается суммарная вероятность;

3)вероятности букв, не участвовавших в объединении, и полученная суммарная вероятность снова располагаются в порядке убывания вероятностей в дополнительном столбце, а две последние буквы снова объединяются.

Процесс продолжается до тех пор, пока не получится единственная вспомогательная буква с вероятностью, равной единице.

В табл. 10 показаны основные шаги построения кода.

Для составления кодовой комбинации, соответствующей данному сообщению, необходимо проследить путь перехода сообщений

49

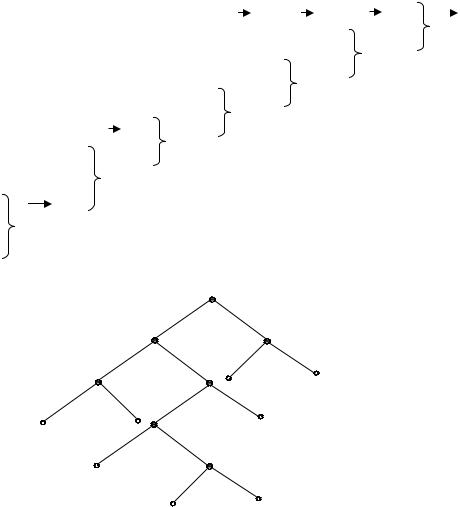
по строкам и столбцам таблицы. Для наглядности строится кодовое дерево (рис. 8).

Таблица 10

Рис. 8. Кодовое дерево

Из точки, соответствующей вероятности 1, направляются две ветви, причем ветви с большей вероятностью присваивается символ

50