УП Информатика

на, если значение функции f(x1, … , xi, … , xn) не изменяется при изменении xi.

Пример логической функции от трех переменных представлен в

Использование фиктивных переменных дает возможность сокращать или расширять количество переменных для логических функций [1].

2.3. Свойства элементарных функций алгебры логики

Элементарные функции типа отрицания, дизъюнкции, Шеффера, Пирса, импликации и т. д. находятся в определенной связи друг с другом.

Конъюнкция, дизъюнкция, отрицание (функции И, ИЛИ, НЕ).

Для них справедливы следующие аксиомы. Пусть x – некоторая логическая переменная. Тогда

1. x = x, что означает возможность исключения из логического выражения всех членов, имеющих двойное отрицание, при замене их исходной величиной;

31

2.x + x = x; xx = x – правила подобных преобразований позволяют сокращать длину логичecкиx выражений;

3.x + 0 = x;

4.x + 1 = 1;

5.x 0 = 0;

6.x · 1 = x;

7.xx = 0 ;

8.x + x = 1.

Дизъюнкция и конъюнкция обладают рядом свойств, аналогичных свойствам обычных арифметических операций сложения и умножения:

1) свойство ассоциативности (сочетательный закон): для дизъюнкции

x1 + (x2 + x3) = (x1 + x2) + x3,

для конъюнкции

x1 (x2 x3) = (x1 x2) x3;

2) свойство коммутативности (переместительный закон): для дизъюнкции

x1 + x2 = x2 + x1,

для конъюнкции

x1 x2 = x2 x1;

3) свойство дистрибутивности (распределительный закон) определяет правила раскрытия скобок или взятия в скобки логических выражений:

для конъюнкции относительно дизъюнкции

x1&(x2 + x3) = (x1&x2) + (x1&x3);

32

для дизъюнкции относительно конъюнкции

x1 + x2 x3 = (x1 + x2) & (x1 + x3).

П р и м е р . Доказать, что x1 + x2 x3 = (x1 + x2)& (x1+ x3). Д о к а з а т е л ь с т в о .

(x1 + x2) (x1+ x3) = x1x1+ x1x3 + x1x2 + x2x3 = x1 + x1x2 + x1x3 + x2x3 =

= x1 (1+ x2 + x3) + x2 x3 = x1 + x2 x3 .

Аналогично с помощью вышеизложенных аксиом можно доказать и другие законы.

Законы де Моргана, с помощью которых можно выражать конъюнкцию через дизъюнкцию и отрицание или дизъюнкцию через конъюнкцию и отрицание.

x1x2 = x1 + x2 ,

x1 + x2 = x1x2 .

Следствия, вытекающие из законов де Моргана:

x1x2 = x1 + x2 , x1 + x2 = x1x2 .

Законы де Моргана и следствия из них справедливы для любого количества переменных:

x1 + x2 + ... + xn = x1 & ... & xn ,

x1x2 ...xn = x1 + x2 + ... + xn .

33

Законы поглощения:

x1 + x1x2 = x1,

x1 ( x1 + x2 ) = x1 .

Закон склеивания:

(x1 x2 ) + (x1 x2 ) = x1 .

Закон склеивания применяется в том случае, когда две конъюнкции, соединенные знаком дизъюнкции, содержат одинаковое количество одних и тех же переменных, причем одна из них входит в одну из конъюнкций с отрицанием, а в другую – без отрицания. Тогда по этой переменной производится «склеивание». В результате вместо двух конъюнкций остается одна, в которой на одну переменную меньше.

Функция сложения по модулю 2 выражается следующим обра-

зом:

x1 Å x2 = x1x2 + x1x2 = ( x1 + x2 ) ( x1 + x2 ) .

Свойства функции сложения по модулю 2:

1) коммутативности (переместительный закон):

x1 Å x2 = x2 Å x1;

2) ассоциативности (сочетательный закон):

x1 Å( x2 Å x3 ) = ( x1 Å x2 ) Åx3 ;

3) дистрибутивности (распределительный закон):

x1 ( x2 Å x3 ) = ( x1x2 ) Å ( x1x3 ).

34

Для этой функции справедливы аксиомы:

x Å x = 0; x Å 1 = x ; x Å x = 1; x Å 0 = x.

Функция НЕ, выраженная через функцию сложения по модулю 2, имеет вид

x1 = x1 Å1.

Функция ИЛИ, выраженная через функцию сложения по модулю 2, имеет вид

x1 + x2 = x1 Å x2 Å x1x2 .

Функция И, выраженная через функцию сложения по модулю 2, имеет вид

( x1 Å x2 ) Å ( x1 + x2 ).

Функция импликации (→) выражается следующим образом:

x1 ® x2 = x1 + x2 .

Для функции импликации справедливы следующие аксиомы:

x ® x = 1; x ®1 = 1; 0 ® x = 1; x ® x = x ; x ® 0 = x ; 1 ® x = x .

Из аксиом следует, что импликация обладает только свойством коммутативности (переместительный закон) в измененном виде:

x1 ® x2 = x2 ® x1 .

Свойство ассоциативности для этой функции несправедливо. Функция ИЛИ, выраженная через функцию импликации:

35

x1 + x2 = x1 → x2 .

Функция И, выраженная через функцию импликации:

x1x2 = x1 → x2 .

Функция НЕ, выраженная через функцию импликации:

x1 = x1 → 0.

Функция Шеффера (/) может быть выражена соотношением

x1 / x2 = x1x2 .

Для нее справедливы аксиомы:

x / x = x ; x / x = 1; x / 0 = 1;

x / 1 = x ; x / 0 = 1; x / 1 = x .

Эти аксиомы позволяют сформулировать следующие правила преобразования:

x1x2 = x1 / x2 = ( x1 / x2 ) / ( x1 / x2 ) ;

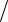x = x x ;

x1 + x2 = x1 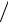x2 = ( x1 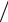x1 ) ( x2 x2 ) .

Для функции Шеффера справедливо свойство коммутативности для двух переменных x1 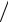x2 = x2 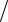x1 , что легко проверяется. Для трех и более переменных это свойство уже не выполняется.

36

З а м е ч а н и е . Функция Шеффера является строго двухместной функцией, т. е. для нее невозможны записи вида x1 x2 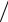x3 или x1 x2 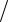... xn , так как непонятно, в какой очередности применять операцию Шеффера в этом выражении. Следовательно, очередность применения операции Шеффера должна указываться с помощью скобок.

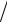П р и м е р . ( ( x1 x2 ) x3 )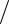x4 или ( x1 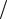x2 )( x3 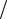x4 ) .

Свойства ассоциативности и дистрибутивности функции Шеффера несправедливы для трех переменных, а следовательно, несправедливы и для n переменных.

Функция Пирса (Вебба) (↓) описывается выражением

x1 ↓ x2 = x1 + x2 = x1x2 .

Для функций Пирса (Вебба) справедливы аксиомы:

Элементарные булевы функции И, ИЛИ, НЕ выражаются через функцию Пирса (Вебба) следующим образом:

функция НЕ:

x = x ↓ x ;

функция И:

x1x2 = ( x1 ↓ x1 ) ↓ ( x2 ↓ x2 );

37

функция ИЛИ:

x1 + x2 = ( x1 ↓ x2 ) ↓ ( x1 ↓ x2 ).

Для функции Пирса (Вебба) справедливо свойство коммутативности только для двух переменных: x1 ↓ x2 = x2 ↓ x1. Функция Пирса (Вебба), так же как и функция Шеффера, является двухместной функцией. Следовательно, невозможны записи вида:

x1 ↓ x2 ↓ x3 ↓ ... ↓ xn ;

для установления приоритетов обязательно должны использоваться скобки, которые определяют последовательность осуществления операций:

( x1 ↓ x2 ) ( x3 ↓ ( x4 ↓ x5 ) ).

свойств у этих функций [1].

2.4. Аналитическое представление функций алгебры логики

Существует много способов задания логических функций. Ранее был рассмотрен табличный способ, при котором каждому набору значений переменных в таблице истинности указывается значение самой логической функции. Этот способ нагляден и может быть применен для записи функций от любого количества переменных. Однако при анализе свойств функций алгебры логики (ФАЛ) такая запись не является компактной. Проще выглядит аналитическая запись в виде формул.

38

Рассмотрим фиксированный набор переменных { x1 , x2 , …, xn } , на котором задана функция алгебры логики. Так как любая переменная xi = { 0 , 1} , то набор значений переменных фактически

представляет собой некоторое двоичное число. Представим, что номером набора будет произвольное двоичное число, получаемое следующим образом:

i = 2n−1 x1 + 2n−2 x2 + ... + xn .

Пусть имеется функция Фi ( x1, x2 , ..., xn ) :

0, если номер набора равен i;

Фi =

1, если номер набора не равен i.

Функцию Фi называют термом.

Дизъюнктивный терм – терм, связывающий все переменные, представленные в прямой или инверсной форме, знаком дизъюнкции.

П р и м е р . Ф1 = x1 x2 x3 x4 ; Ф2 = x1 x2.

Конъюнктивный терм – терм, связывающий переменные, представленные в прямой или инверсной форме, знаком конъюнкции. Обозначается конъюнктивный терм следующим образом:

П р и м е р . F1 = x1 x2 x3 x4 ; F0 = x1 x2 x3.

Ранг терма r определяется количеством переменных, входящих в данный терм.

39

П р и м е р . Для конъюнктивного терма F1 = x1 x2 x3 x4 x5 r = 5 , для дизъюнктивного терма Ф2 = x1 + x2 + x3 r = 3 .

Любая таблично заданная функция алгебры логики может быть представлена аналитически в виде

где i – номера наборов, на которых функция равна 1; – знак дизъ-

1

юнкции, объединяющий все термы Fi , равные единице.

Таблица истинности однозначно отображается аналитической записью вида (1), которую называют объединением термов.

Нормальная дизъюнктивная форма (НДФ) – объединение тер-

мов, включающее конъюнктивные термы переменного ранга. Количество всех термов, входящих в состав (1), равно количест-

ву единичных строк таблицы [1].

П р и м е р . Записать в аналитическом виде функцию, заданную табл. 5.

Р е ш е н и е . На основании (1) эту функцию можно записать в аналитической форме:

f ( x1, x2 , x3 ) = F ( 0, 0, 0 ) + F ( 0, 1, 1) + F (1, 0, 0 ) = x1x2 x3 + x1x2 x3 + x1x2 x3 .

Ответ: f ( x1, x2 , x3 ) = x1x2 x3 + x1x2 x3 + x1x2 x3 .

40