3.4. Мода и медиана

Модой случайной величины X дискретного типа называется такое возможное значение , для которого

, (3.14)

т.е. это то значение д.с.в., которое имеет наибольшую вероятность, если такое значение единственно. Мода может не существовать, иметь единственное значение (унимодальное распределение), иметь множество значений (мультимодальное распределение).

Модой случайной величины X непрерывного типа называется действительное число , определяемое как точка максимума плотности распределения вероятностей.

Медианой непрерывной случайной величины X называется действительное число 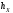, удовлетворяющее условию

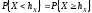, (3.15)

т.е. корень уравнения

. (3.16)

Так как данное уравнение может иметь множество корней, то медиана определяется, вообще говоря, неоднозначно.

4. Различные законы распределения случайной величины

4.1. Биномиальное распределение дискретной случайной величины

Пусть эксперимент проводится n раз и имеет 2 исхода: У – успех, Н - неудача. Р(У)= р ; Р(Н)=1- р = q (испытания Бернулли).

Пусть Х - случайная величина - это количество успехов в серии n испытаний и 0,1,2,...n - возможное значение случайной величины. Тогда вероятность того, что случайная величина примет значение, равное k, можно найти по формуле

- (4.1)

биномиальное распределение, оно задаётся вероятностью отдельного успеха р и числом испытаний n.

Числовые характеристики:

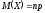, (4.2)

4.2. Распределение Пуассона

Во многих задачах приходится иметь дело с испытаниями Бернулли, в которых n велико, а р - мало, т.е. каждый успех - это редкое событие, но среднее число успехов довольно значительно. В этом случае удобнее переходить к формуле

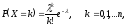(4.3)

которая называется формулой распределения Пуассона и получается из формулы биномиального распределения при ии условии, чтосохраняет постоянное значение при повторении эксперимента.

Числовые характеристики:

;. (4.4)

Замечание: при n > 100 и np < 30 от формулы Бернулли переходят к формуле Пуассона.

4.3. Равномерное распределение случайной величины на отрезке

Непрерывная случайная величина Х называется равномерно распределённой на отрезке [a, b], если её плотность вероятности постоянна на этом отрезке и равна 0 вне его, т.е.:

(4.5)

Пользуясь формулой (1.6), можно найти функцию распределения :

(4.6)

Числовые характеристики:

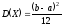; .(4.7)