3. Числовые характеристики случайных величин

3.1. Математическое ожидание

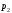Задача. Пусть имеется игра (например, лотерея), в которой можно выиграть некоторую сумму с вероятностью,с вероятностью,…с вероятностью. Средиможет быть нулевое значение – отсутствие выигрыша и отрицательное – проигрыш. Таким образом, выигрыш в игре можно рассматривать как дискретную случайную величинуX, ряд которой задается числами и.

Вопрос: Насколько выгодна игра, т.е. каково “среднее ожидаемое” значение выигрыша?

Это можно представить так. Пусть некто участвует в игре достаточно большое число раз N и - количество получений выигрыша. Тогда общий суммарный выигрышN игр составит

,

а средний выигрыш за одну игру

,

где- частота событиявN испытаниях.

Если имеется статистическая устойчивость, то по статистическому определению вероятности при достаточно большом N частота события приближенно равна соответствующей вероятности, т.е.

,

а средний выигрыш приближенно равен:

.

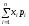В теории вероятности его называют математическим ожиданием случайной величины X.

Математическим ожиданием дискретной случайной величины X, имеющей n возможных значений , называется число:

, (3.1)

где .

Если множество значений дискретной случайной величины бесконечно (счетно), то сумма (1) задается рядом

, (3.2)

который сходится абсолютно.

Математическим ожиданием непрерывной случайной величины X, имеющей плотность вероятности , называется число:

- (3.3)

интеграл сходится абсолютно.

Замечание. Если ряд (2) и интеграл (3) не сходятся, то математического ожидания случайной величины не существует.

Математическое ожидание характеризует “среднее” значение случайной величины. Так, если случайная величина есть ошибка измерения некоторой физической величины, т.е. разность между показаниями прибора и истинным значением, то случай, когда >0 означает, что “в среднем” прибор будет давать завышенные показания, а<0 – заниженные. Таким образом, математическое ожидание ошибки измерения можно назвать систематической ошибкой. Отсутствие ошибки:=0.

Механический смысл:

Закон распределения можно интерпретировать как расположение на прямой в точках точечных масс, равных, где. В этом случае- центр масс (центр тяжести). Аналогично интерпретируется формула (3): здесь единичная масса непрерывно распределена вдоль осиOx с линейной плотностью .

Свойства математического ожидания:

1° если X=С – const, то ,

2° ,

3° ,

4° если X и Y – независимые случайные величины, то .

3.2. Дисперсия

Дисперсией случайной величины X называется число, обозначаемое 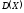и равное математическому ожиданию квадрата разности между случайной величиной и ее математическим ожиданием:

. (3.4)

Дисперсия вычисляется по формулам:

Механический смысл:

- это момент инерции масс относительно центра тяжести. Таким образом,характеризует место, вокруг которого группируются массы, а- степень разбросанности массоколо.

Свойства дисперсии:

1° >0,

2° если X=С – const, то ,

3° ,

4° если X и Y – независимые случайные величины, то .

Наряду с дисперсией, имеющей размерность квадрата случайной величины, для той же цели используется так называемое среднеквадратичное отклонение случайной величины:

, (3.7)

имеющее одну размерность со случайной величиной X.

Для вычисления также удобно пользоваться формулами:

где .

Примеры.

1. Подбрасывается игральная кость. Случайная величина X – число выпадений очков. Найти математическое ожидание и дисперсию с.в.

◄.

.

2. X – непрерывная случайная величина с заданной плотностью вероятности .

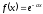Найти 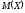для.

◄