
- •2.Случайные величины
- •2.1. Дискретные случайные величины. Закон распределения дискретных случайных величин.
- •2.2. Функция распределения случайной величины.
- •2.3. Непрерывные случайные величины. Плотность распределения вероятности случайной величины.
- •3. Числовые характеристики случайных величин
- •3.1. Математическое ожидание
- •3.2. Дисперсия
- •3.4. Мода и медиана
- •4. Различные законы распределения случайной величины
- •4.1. Биномиальное распределение дискретной случайной величины
- •4.2. Распределение Пуассона
- •4.3. Равномерное распределение случайной величины на отрезке
- •4.4. Показательное распределение случайной величины
- •4.5. Нормальное распределение случайной величины
- •4.6. Вероятность попадания в интервал:
2.Случайные величины
Под случайной величиной понимают переменную величину, которая может принимать то или иное значение, в зависимости от хода испытаний. Обозначается X или Y.
Если
говорят, что задача случайна X,
то предполагается, что имеется испытание,
в котором наблюдается эта величина, и
существуют
вероятности событий вида:
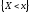 ,
,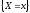 ,
,
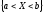 ,
где x,
a,
b
,
где x,
a,
b R.
Случайный характер случайных величин
проявляется в том, что различные значения
она может принимать с теми или иными
вероятностями.
R.
Случайный характер случайных величин
проявляется в том, что различные значения
она может принимать с теми или иными
вероятностями.
Зависимость между возможными значениями случайных величин и соответствующими вероятностями называется законом распределения случайных величин.
2.1. Дискретные случайные величины. Закон распределения дискретных случайных величин.
Дискретной случайная величина называется такую случайную величину, множество возможных значений которой либо конечное, либо бесконечное, но счетное.
Пусть
X
-
дискретная случайная величина, имеющая
n
различных значений
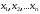 .
.
Равенства
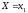 ,
,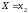 ,…
,… являются событиями, а, значит, имеют
некоторую вероятность. Обозначим
являются событиями, а, значит, имеют
некоторую вероятность. Обозначим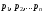 вероятностиэтих
событий, т.е.
вероятностиэтих
событий, т.е.
 ,
,
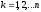 .
.
Функциональная зависимость между возможными значениями случайной величины и соответствующими вероятностями – простейшая форма закона распределения дискретных случайных величин, а ее табличное представление называется рядом распределения дискретных случайных величин:
|
xk |
x1 |
x2 |
… |
xn |
|
pk |
p1 |
p2 |
… |
pn |
Т.к. события образуют полную группу, то
 .
(2.1)
.
(2.1)
Если
множество значений дискретных случайных
величин бесконечно (счетно), то сумма в
формуле (1.1) заменяется
рядом
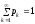 ,
при этом ряд не может быть представлен
таблицей.
,
при этом ряд не может быть представлен
таблицей.
2.2. Функция распределения случайной величины.
Функцией распределения случайной величины Х называется функция, ставящая в соответствии каждому значению аргумента х вероятность того, что случайная величина Х примет значение, меньше, чем х:
 (2.2)
(2.2)
Зная функцию распределения случайной величины можно найти вероятность попадания случайной величины в любой интервал:
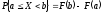 .
(2.3)
.
(2.3)
График
функции распределения 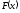 дискретной
случайной величины
представляет собой график неубывающей
функции, значения которой начинаются
от 0 и доходят до 1, причем в точках
дискретной
случайной величины
представляет собой график неубывающей
функции, значения которой начинаются
от 0 и доходят до 1, причем в точках
 функция имеет разрывы первого рода
(скачки) (рис.1).
функция имеет разрывы первого рода
(скачки) (рис.1).
Свойства функции распределения случайной величины:
1°
 ,
т.к. F(x)
– вероятность (
,
т.к. F(x)
– вероятность (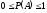 );
);
2°
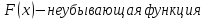
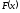 -
неубывающая функция;
-
неубывающая функция;
3°

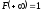 ;
доказательство:
;
доказательство: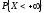 -
достоверное событие;
-
достоверное событие;
4°
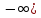
 ;
доказательство: т.к.
;
доказательство: т.к.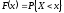 ,
то
,
то
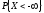 - невозможное
событие.
- невозможное
событие.

F(x)
Рис.1
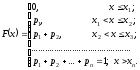
2.3. Непрерывные случайные величины. Плотность распределения вероятности случайной величины.
Случайная величина называются непрерывной, если ее возможные значения сплошь заполняют конечный или бесконечный промежуток.
Теорема:
Если
функция распределения непрерывна в
точке
 ,
то
,
то
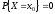 .
(2.4)
.
(2.4)
Отсюда
следует (ф. 2.3)), что если функция непрерывна
в точке
 ,
то
,
то
 ,
,
 .
(2.5)
.
(2.5)
Замечание:
Если функция
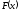 непрерывна в точкеb,
то оба строгих неравенства в формуле
(2.5) можно заменить нестрогими.
непрерывна в точкеb,
то оба строгих неравенства в формуле
(2.5) можно заменить нестрогими.
Если
функция распределения
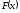 дифференцируема
для всех x
дифференцируема
для всех x R
то
ее производная
R
то
ее производная
 (2.6)
(2.6)
называется плотностью распределения вероятности случайной величины X.
Согласно
определению,
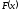 является первообразной для плотности
вероятности случайной величины
является первообразной для плотности
вероятности случайной величины
 :
:
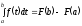 ,
,
следовательно:

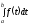 .
(2.7)
.
(2.7)
Из
геометрического смысла определенного
интеграла следует, что вероятность
попадания непрерывной случайной величины
Х
в заданный интервал равна площади
криволинейной трапеции S,
ограниченной осью абсцисс, прямыми
 ,
графиком функции
,
графиком функции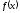 ,
который называется кривой распределения
вероятностей (рис.2).
,
который называется кривой распределения
вероятностей (рис.2).
Полагая
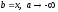 ,
получим
,
получим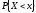 ,
т.е. формулу для вычисления функции
распределения непрерывной случайной
величины:
,
т.е. формулу для вычисления функции
распределения непрерывной случайной
величины:
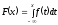 .
(2.8)
.
(2.8)
Свойства плотности распределения:
1°
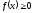 ;
;
2°
 - свойство нормировки.
- свойство нормировки.

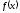

Рис.2
