Систему уравнений (2) можно записать иначе

Коэффициенты С_ij называют частичными емкостями на единицу длины.

Если провода линии не связаны с Землей и питаются от незаземленного источника ЭДС, то суммарный заряд линии равен нулю, т.е. τ₂ = –τ₁.

φ₁ = (α₁₁ – α₁₂) τ₁, φ₂ = (α₂₁ – α₂₂) τ₁

Вычтем второе уравнение из первого и получим

U =φ₁ – φ₂ = (α₁₁ + α₂₂ – α₂₁ – α₁₂) τ₁

Отношение линейной плотности заряда провода к напряжению называют в данном случае рабочей емкостью линии на единицу длины

C_раб = τ/U =(α₁₁ + α₂₂ – α₂₁ – α₁₂)^-1 (3)

Можно изобразить эквивалентную схему системы заряженных проводников линии (рис. 10).

Рис. 10.

Анализируя эту схему, можно получить другое выражение для рабочей емкости линии

C_раб = C₁₂ + C₁₁C₂₂/(C₁₁ + C₂₂) (4)

Можно доказать, что выражения (3) и (4) тождественны.

Ниже представлен текст вычислительного сценария расчёта потенциальных и ёмкостных коэффициентов, а также частичных ёмкостей многопроводной воздушной линии с учётом влияния земли.

% ElStatLin - Расчёт потенциальных и емкостных коэффициентов многопроводной линии.

% Смещение электрических осей относительно геометрических не учитываетсq.

% Входные параметры:

% x - горизонтальные координаты подвеса проводов;

% y - вериткальные координаты подвеса проводов;

% D - диаметры всех проводов

% Все эти переменные - строковые матрицы

% Выходные параметры:

% al - потенциальные коэффициенты проводов;

% be - ёмкостные коэффициенты проводов;

% c - частичные ёмкости проводов

eps0=8.85e-12; % Абcолютнаq диэлектрическаq проницаемость вакуума, Ф/м

rp=sqrt((repmat(x,length(x),1)-repmat(x,length(x),1).').^2+...

(repmat(y,length(y),1)-repmat(y,length(y),1).').^2)+diag(D/2);

rm=sqrt((repmat(x,length(x),1)-repmat(x,length(x),1).').^2+...

(repmat(y,length(y),1)+repmat(y,length(y),1).').^2);

al=log(rm./rp)/eps0/2/pi % Потенциальные коэффициенты, м/Ф

be=inv(al) % Ёмкостные коэффициенты, Ф/м

c=diag(sum(be))+diag(diag(be))-be % Частичные ёмкости, Ф/м

Распределение зарядов и потенциалов в системе заряженных проводников

Пусть имеется система из n заряженных проводников: q_i(i = 1,…, n ) – заряды проводников, φ_i (i = 1,…, n ) – потенциалы проводников.

Потенциалы проводников можно представить в виде линейной комбинации их зарядов.

φ_i = α_ij q_j;

или

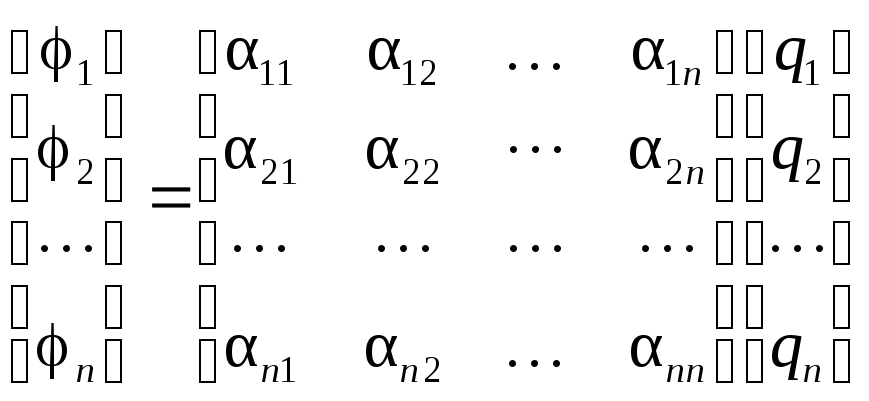
или

[φ^(п)] = [α] [q^(п)]

Коэффициенты α_ij называются потенциальными коэффициентами системы проводников и измеряются в 1/Ф.

Из последнего матричного уравнения можно выразить заряды проводников

[q^(п)] = [α]^-1 [φ^(п)] = [β] [φ^(п)]

или

,

т. е. q_i = β_ij φ_j ;

Коэффициенты β_ij называются емкостными коэффициентами системы проводников и измеряются в Ф.

Последнее соотношение можно записать иначе

q_i = С_iiφ_i +С_ij (φ_i – φ_j);

С_ij – это частичные емкости системы проводников.

C_ii = β_ij – собственные частичные емкости

C_ij (j i)= – β_ij – взаимные частичные емкости.

Матрицы [α], [β], [C] симметричные, т.е. α_ij = α_ji, β_ij = β_ji, C_ij = C_ji.Значит, для системы заряженных проводников выполняется принцип взаимности.

Электростатические экраны

Принцип электростатического экранирования электрических и электронных элементов в аппаратуре основан на том, что медленно изменяющееся электрическое поле не может проникнуть внутрь объема, ограниченного проводником, поскольку любая поверхность электропроводящего тела в электростатическом поле является эквипотенциальной.