Расчёт и визуализация поля электрического диполя в системе matlab

Ниже представлен текст вычислительного сценария MATLAB, предназначенного для расчёта названного поля.

% el_dipol - Расчёт о визуализация поля электрического диполя

% Электрический дипольный момент направлен вдоль оси y

% Рассчитывается распределение скалярного электрического потенциала

% и компонентов вектора напряжённости электрического поля

P=1; % y-компонента электрического дипольного момента, пКл*м

eps0=8.854; % Абсолютная диэлектрическая проницаемость вакуума, пФ/м

[x,y]=meshgrid(0.1:0.01:0.5,0.1:0.01:0.5);

fi=P*y./(4*pi*eps0*(x.^2+y.^2).^1.5);

Ex=3*P*y.*x./(4*pi*eps0*(x.^2+y.^2).^2.5);

Ey=P*(3*y.^2./(x.^2+y.^2)+1)./(x.^2+y.^2).^1.5/(4*pi*eps0);

E=sqrt(Ex.^2+Ey.^2);

figure(1)

contour(x,y,fi,19)

grid on

figure(2)

contour(x,y,Ex,29)

grid on

figure(3)

contour(x,y,Ey,29)

grid on

figure(4)

contour(x,y,E,29)

grid on

Ниже показано содержимое фигур MATLABс изолиниями потенциала и компонентов вектора напряжённости электрического поля.

Поле бесконечно длинной заряженной оси

Пусть имеется бесконечно длинная заряженная ось, имеющая заряд на единицу длины τ (рис. 2).

Рис. 2.

Охватим эту ось цилиндрической поверхностью, ось которой совпадает с заряженной осью. На этой поверхности вектор электрического смещения имеет только нормальную составляющую D_n, причем D_n = const. В соответствии с теоремой Гаусса в интегральной форме

DdS = D_ndS = D_nS = D_n2πrl = τl,

откуда D = D_n = D_r= τ/(2πr)

E = E_r= τ/(2πε₀εr)

E = – grad φ

E = –

φ = – Edr

φ = – τdr/(2πε₀εr) = – τ/(2πε₀ε)ln(r) + A

Во многих практических случаях электрическое поле можно представить в виде линейной комбинации полей нескольких заряженных осей или нескольких пар разноименно заряженных осей. Поэтому целесообразно рассмотреть поле одной такой пары.

Контрольные вопросы

1. Какими соотношениями описывается поле электрического диполя?

2. Какие поля называются плоскомеридианными (осесимметричными)?

3. Какими соотношениями описывается поле бесконечно длинной заряженной оси?

§ 2.3. Электростатические поля простых двухпроводных линий Поле двух разноименно заряженных осей

Пусть в однородном диэлектрике находятся две параллельные бесконечно длинные оси, равномерно и разноименно заряженные с линейной плотностью заряда +τ и – τ (рис. 3). Изобразим на рисунке следы этих осей в плоскости поперечного сечения

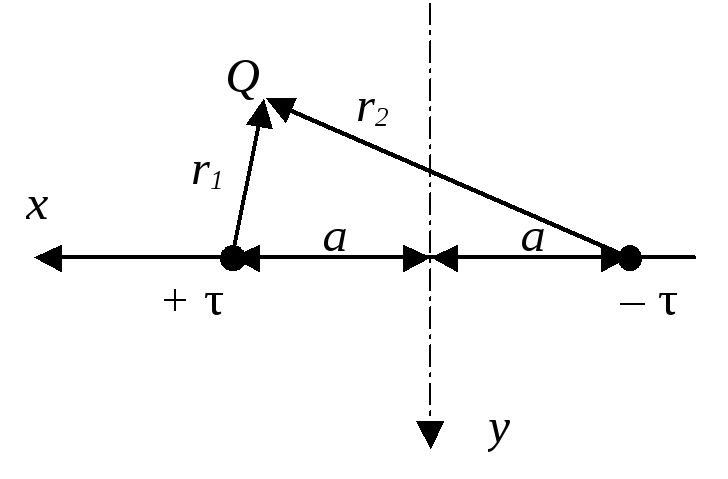
Рис. 3.

φ(Q) = φ₊ + φ_- = – τ/(2πε₀ε)ln(r₁) + τ/(2πε₀ε)ln(r₂) + A = τ/(2πε₀ε)ln(r₂/r₁) + A

Если принять φ(x= 0) = 0, т.е. на оси симметрии. то А =0. Теперь определим уравнение эквипотенциальных поверхностей. На этих поверхностях r₂/r₁=k = const. Здесь k – параметр семейства эквипотенциальных линий в плоскости рисунка.

Выразим r₂ и r₁ в декартовых координатах и выведем уравнение эквипотенциали в канонической форме относительно координат х и у

r₂ = ((x + a) ² + y ²)^0,5; r₁ = ((x – a) ² + y ²)^0,5

(x + a)² + y² = k ² (x – a)² + k ²y ²

(x + a)² – k ² (x – a)² + y²(1 – k ²)= 0

x²(1 – k ²) + 2ax(1 + k ²) + a²(1 – k ²) + y²(1 – k ²) = 0

x² + 2ax(1 + k ²)/(1 – k ²) + y² + a² = 0

(x + a(1 + k ²)/(1 – k ²))² + y² = (a(1 + k ²)/(1 – k ²))² – a² = (2ak/(1 – k ²))²

Здесь получено уравнение окружности в канонической форме:

(x – s)² + y² = R ² (1)

где s = a(k ²+1)/(k ²– 1) – координата центра окружности.

R = a|2k/(1 – k ²)| – радиус окружности.

Мы получили выражения для координаты центра и для радиуса эквипотенциальной линии по задаваемому параметру k, где k = exp(2πεε₀φ/τ).

В соответствии с уравнением (1) линии равного потенциала представляют собой окружности, а поверхности равного потенциала – круговые цилиндры, геометрические оси которых смещены относительно электрических осей. Одна из этих поверхностей вырождается в плоскость с нулевым значением потенциала (при k = 1; s;r).

Линии напряженности представляют собой дуги окружности, начинающиеся на оси с положительным зарядом и кончающиеся на оси с отрицательным зарядом.

Если семейство равнопотенциальных поверхностей рассечь параллельными плоскостями, перпендикулярными заряженным осям, то в каждой плоскости получится одна и та же картина линий. Поля, обладающие таким свойством, называются плоскопараллельными (иначе их называют двумерными полями).

Установив картину поля и использовав следствие теоремы о единственности, можно считать решенными столько новых задач, сколько имеется различных по взаимному расположению пар равнопотенциальных поверхностей, которые можно рассматривать как поверхности проводников.

Рассмотрим важнейшие частные случаи таких задач.