Векторы

1. Основные определения векторного исчисления

   1. Понятие вектора

Векторомназывается направленный отрезок, т. е. отрезок, одна крайняя точка которого (скажем) объявлена началом, а другая концом. Такой вектор обозначается как.Длиной или модулемвектораназывается длина отрезка; она обозначается как. Примерами векторных величин является скорость, ускорение, сила, перемещение. Если, то векторназываетсянулевыми обозначается0. Вектора, два или более, называютсяколлинеарными, если прямые, на которых они лежат, либо параллельны, либо совпадают. Два вектораиназываютсяравными, если их длины равны, они коллинеарны и сонаправлены, т. е. "смотрят" в одну сторону (см. рис. 1). Если вектораине лежат на одной прямой, то их равенство эквивалентно тому, что четырехугольник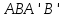есть параллелограмм.

Простое геометрическое построение убеждает нас, что для любого вектора и любой точкисуществует единственная точкатакая, что. Этот векторназывается реализацией векторав точке.

2. Арифметические операции над векторами

Пусть имеются два вектора . Реализуемв точке A:, а векторреализуем в точке B:. Тогда векторназовемсуммой векторов . Это определение корректно, т. е. результат суммы двух векторов не зависит от изначально выбранной точки. Из определения суммы векторов вытекает равенство Шаля:

Равенство Шаля можно обобщить на случай многих векторов:

Существует другое определение операции суммы двух векторов -- правило параллелограмма, но оно "работает" только для не коллинеарных векторов. Пусть имеются два неколлинеарных вектора . Реализуем их в одной точке A, так чтои. Достроимдо параллелограмма. Тогда(см. рис. 2). Результат сложения не зависит от выбора точки. Так какна рис. 2, то сложение по правилу параллелограмма приводит к тому же результату, что и сложение по правилу треугольника.

Умножить вектор на числозначит построить вектортакой, что

1. ;

2. (здесь и далее знак -- символ коллинеарности);

3. если , то и сонаправлены, а если, то и направлены в противоположные стороны. В случаевектор нулевой.

Вектор можно реализовать прямой ℓ в точкекак вектор, где точкастроиться так, что, причем, если>0, то точка D должна лежать по ту же сторону от A, что и точка B; если же<0, то точку D следует выбирать на прямой ℓ по другую сторону от А (см. рис. 3).

Заметим, что из определения умножения вектора на число вытекает, что вектор коллинеарен ненулевому вектору тогда и только тогда, когда для подходящего числа.

Множество всех векторов в пространстве, относительно определенных выше операций сложения и умножения обладает следующими свойствами:

1. (коммутативность);

2. (ассоциативность);

3. (свойство нейтральности нулевого вектора относительно операции сложения);

4. для любого вектора существует противоположный вектортакой, что;

5. (ассоциативность умножения);

6. и(дистрибутивность);

7. (унитарность).

Эти равенства верны для любых векторов и любых действительных чисели μ . Доказательство этого факта весьма длинная и скучная, хотя и элементарная проверка. Коммутативность сложения следует сразу из правила параллелограмма сложения двух векторов (если вектора коллинеарны, то коммутативность сложения векторов следует из коммутативности сложения чисел). Докажем ассоциативность сложения. Реализуем векторaв точке A:, векторреализуем в точке B:, а векторcреализуем в точке C:. Тогда

Здесь четыре раза мы применили равенство Шаля. Правые части равны, значит равенство доказано.

Свойство IVдоказывается так: если, то. Действительно,, где ещё раз применено равенство Шаля. Для того, чтобы доказать свойствоVзаметим сначала, что модули левой и правой частей совпадают с. Ясно также, что векторыилежат на одной прямой и имеют общее начало. Остается убедиться, что они сонаправлены. Это достигается с помощью перебора следующих случаев 1)>0, μ >0, 2)>0, μ <0, 3)<0, μ >0, 4)<0, μ <0, 5) либо=0, либо μ =0. В случаях 1) и 4) вектораисонаправлены с, а поэтому сонаправлены между собой; в случаях 2) и 3) эти вектора сонаправлены с, а поэтому также сонаправлены между собой. В случае 5) эти вектора нулевые.

Свойства IIIиVII-- тривиальности.