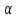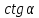Тригонометрические функции
Для
того, что бы определить тригонометрические
функции надо сначала понять, что
подразумевается под длиной кривой,
заданной как совокупность точек
 с координатами
с координатами ,
где
,
где -- параметр, пробегающий некоторый
отрезок
-- параметр, пробегающий некоторый
отрезок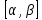 .
Разобьем отрезок
.
Разобьем отрезок значениями
значениями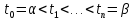 ,
и обозначим это разбиение одной буквой
,
и обозначим это разбиение одной буквой .
Соединим точки
.
Соединим точки последовательно отрезками прямых и
получим(вписанную) ломаную
последовательно отрезками прямых и
получим(вписанную) ломаную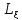 .
Ее длина есть сумма длин звеньев,
составляющих ломаную. Длиной кривой
.
Ее длина есть сумма длин звеньев,
составляющих ломаную. Длиной кривой называется точная верхняя грань длин
ломаных
называется точная верхняя грань длин
ломаных ,
где
,
где пробегает всевозможные разбиения
отрезка
пробегает всевозможные разбиения
отрезка .
Не всегда длина существует. Согласно
аксиоме полноты это имеет место тогда
и только тогда, когда длины вписанных
ломаных ограничены сверху. (Например,
график функции
.
Не всегда длина существует. Согласно
аксиоме полноты это имеет место тогда
и только тогда, когда длины вписанных
ломаных ограничены сверху. (Например,
график функции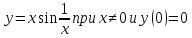 на отрезке
на отрезке имеет бесконечную длину каково бы
имеет бесконечную длину каково бы мы ни взяли). Однако, если график
непрерывной функции
мы ни взяли). Однако, если график
непрерывной функции выпукл на отрезке
выпукл на отрезке ,
то он имеет длину. Для верхней
полуокружности
,
то он имеет длину. Для верхней
полуокружности это так. Более того заменяя звено
вписанной ломаной на катеты прямоугольного
треугольника, построенного на этом
звене как на гипотенузе и имеющего
стороны параллельные координатным
осям, легко находим, что длина полуокружности
единичного радиуса
это так. Более того заменяя звено
вписанной ломаной на катеты прямоугольного
треугольника, построенного на этом
звене как на гипотенузе и имеющего
стороны параллельные координатным
осям, легко находим, что длина полуокружности
единичного радиуса .
Более точные вычисления дают значение
.
Более точные вычисления дают значение .
Обозначим длину полуокружности единичного
радиуса как
.
Обозначим длину полуокружности единичного
радиуса как .
Имеем
.
Имеем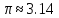 .
Еще точнее результатЦзу
Чунчжи(V веке н. э.) — китайского
астронома и математика, --
.
Еще точнее результатЦзу
Чунчжи(V веке н. э.) — китайского
астронома и математика, -- (выделены верные знаки).
(выделены верные знаки).
 — трансцендентное
число, то есть оно не может
быть корнем какого-либо
многочлена с целыми коэффициентами.
Трансцендентность числа
— трансцендентное
число, то есть оно не может
быть корнем какого-либо
многочлена с целыми коэффициентами.
Трансцендентность числа  была
доказана в 1882
годупрофессором КёнигсбергскогоЛиндеманом.
Доказательство упростил Феликс
Клейнв 1894 году. Поскольку в евклидовой
геометрииплощадькруга и длинаокружности являются
функциями числа
была
доказана в 1882
годупрофессором КёнигсбергскогоЛиндеманом.
Доказательство упростил Феликс
Клейнв 1894 году. Поскольку в евклидовой
геометрииплощадькруга и длинаокружности являются
функциями числа ![]() ,
то доказательство трансцендентности
,
то доказательство трансцендентности положило
конец спору о квадратуре
круга, длившемуся более 2,5 тысяч лет
(построить с помощью циркуля и линейки
квадрат равновеликий заданному кругу).
положило
конец спору о квадратуре
круга, длившемуся более 2,5 тысяч лет
(построить с помощью циркуля и линейки
квадрат равновеликий заданному кругу).
Напомним
определение тригонометрических функций.
Тригонометрической окружностьюназовем окружность на декартовой
плоскости ,
имеющая единичный радиус с центр в
начале координат. Она задается уравнением
,
имеющая единичный радиус с центр в
начале координат. Она задается уравнением .
Вращение против часовой стрелки назовем
положительным, а по часовой стрелке –
отрицательным. Пусть задано число
.
Вращение против часовой стрелки назовем
положительным, а по часовой стрелке –
отрицательным. Пусть задано число Если
Если ,
то пройдем по тригонометрической
окружности от точки
,
то пройдем по тригонометрической
окружности от точки расстояние равное
расстояние равное в положительном направлении. Если же
в положительном направлении. Если же ,
то пройдем расстояние
,
то пройдем расстояние в отрицательном направлении. В итоге
приходим в некоторую точку
в отрицательном направлении. В итоге
приходим в некоторую точку .
Абсцисса этой точки называется косинусом
числа
.
Абсцисса этой точки называется косинусом
числа и обозначается
и обозначается ,
а ордината этой точки есть синус числа
,
а ордината этой точки есть синус числа (обозначается
(обозначается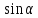 ).
Из определения этих функций и теоремы
Пифагора следуетосновное
тригонометрическое тождество:
).
Из определения этих функций и теоремы
Пифагора следуетосновное
тригонометрическое тождество:

Тогда тангенс и котангенс определяются так:

а секанс и косеканс определяются так:

Построим
луч
 .
В точках с координатами
.
В точках с координатами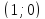 и
и востановим перпендикуляры к осям
востановим перпендикуляры к осям и
и соответственно. Тогда все тригонометрические
функции (острого) угла
соответственно. Тогда все тригонометрические
функции (острого) угла совпадают с длинами отрезков, указанных
на рисунке выше.
совпадают с длинами отрезков, указанных
на рисунке выше.
Таблица значений тригонометрических функций
|
|
0°(0 рад) |
30° (π/6) |
45° (π/4) |
60° (π/3) |
90° (π/2) |
180° (π) |
270° (3π/2) |
360° (2π) |
|
|
0 |
|
|
|
1 |
0 |
-1 |
0 |
|
|
1 |
|
|
|
0 |
-1 |
0 |
1 |
|
|
0 |
|
1 |
|
|
0 |
|
0 |
|
|
|
|
1 |
|
0 |
|
0 |
|
Некоторые формулы приведения:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Формулы сложения



![]()

![]()
Формулы для кратных углов
Формулы двойного угла:
![]()
![]()
Формулы тройного угла:
![]()
![]()
![]()
![]()
Прочие формулы для кратных углов:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()