
Параболы. Гипербола.
График функции
 или,
более общо,
или,
более общо, называется параболой. У параболы
называется параболой. У параболы точка
точка есть точка глобального минимума, т.е.
в ней достигается наименьшее значение,
равное
есть точка глобального минимума, т.е.
в ней достигается наименьшее значение,
равное
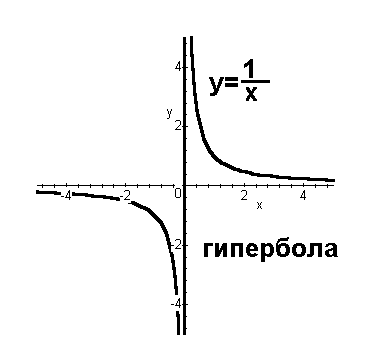

Рисунок 2. Параболы
Рисунок 3. Гипербола
нулю.
Кубическая парабола
 в точке
в точке касается
оси
касается
оси ,
однако возрастает в этой точке и вообще
на всей числовой оси; сама точка
,
однако возрастает в этой точке и вообще
на всей числовой оси; сама точка будет точкой перегиба.
будет точкой перегиба.
Гипербола
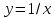 терпит разрыв в нуле, график этой функции
имеет две ветви. Каждая из ветвей на
бесконечности сколь угодно близко
подходит к оси Ох.
терпит разрыв в нуле, график этой функции
имеет две ветви. Каждая из ветвей на
бесконечности сколь угодно близко
подходит к оси Ох.
Показательные и логарифмические функции
Ранее
была определена степень с натуральным
и отрицательным целым показателем, а
также арифметический корень n-ой степени.
В связи с этим отметим, что
 ,
хотя и
,
хотя и ,
но -3 не является неотрицательным числом.
,
но -3 не является неотрицательным числом.
Для
любого неотрицательного числа
 и натурального n степень
и натурального n степень есть арифметический корень
есть арифметический корень .
Например,
.
Например,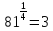 .
Степень с рациональным показателем m/n
, где n∈ℕ,
а m -- целое число, получается как комбинация
двух предыдущих:
.
Степень с рациональным показателем m/n
, где n∈ℕ,
а m -- целое число, получается как комбинация
двух предыдущих:

Свойства степеней следующие.
(основное свойство)
 ;
; ,
в частности
,
в частности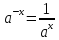 ;
; ;
; ,
,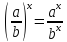 ;
;если
 ,
то
,
то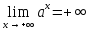 и
и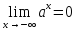 ;
если же
;
если же ,
то
,
то и
и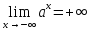
Эти
свойства сначала доказываются для целых
показателей, а затем для рациональных
показателей. Доказательства при этом
чисто алгебраические, без использования
предела (кроме последнего свойства). В
связи с последним свойством заметим,
что можно доопределить операции с
бесконечностью, полагая для
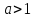

а
для
 наоборот:
наоборот:

Но
операция
 остается неопределенной.
остается неопределенной.
Лемма.
Пусть и
и .
Тогда найдется
.
Тогда найдется такое, что
такое, что .
.
Доказательство
сводим к неравенству
 для заданного положительного𝜺. При достаточно большом натуральном
n имеет место неравенство
для заданного положительного𝜺. При достаточно большом натуральном
n имеет место неравенство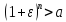 (см. принцип Архимеда). Следовательно,
если взять Δ =1/n, то
(см. принцип Архимеда). Следовательно,
если взять Δ =1/n, то в силу монотонности корня.
в силу монотонности корня.
Теорема.Для всякого положительного числа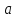 не равного единице, имеется единственная
непрерывная строго монотонная функция
не равного единице, имеется единственная
непрерывная строго монотонная функция ,
удовлетворяющая перечисленным выше
свойствам и совпадающая с
,
удовлетворяющая перечисленным выше
свойствам и совпадающая с для рационального
для рационального .
.
Доказательство.
Считаем
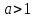 .
Пусть
.
Пусть .
Определим
.
Определим

В
силу леммы монотонность сохраняется:
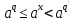 для
любых рациональных
для
любых рациональных .
Отсюда следует непрерывность. Аналогично
разбирается случай
.
Отсюда следует непрерывность. Аналогично
разбирается случай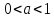 .
.
Докажем
первое свойство функции
 .
Пусть
.
Пусть . Выберем последовательности
. Выберем последовательности рациональных точек, сходящиеся к
рациональных точек, сходящиеся к и
и соответственно
(например, приближения по недостатку
бесконечных десятичных дробей
соответственно
(например, приближения по недостатку
бесконечных десятичных дробей и
и ).
Далее воспользуемся непрерывностью и
свойством 1 в том случае, когда показатели
рациональны:
).
Далее воспользуемся непрерывностью и
свойством 1 в том случае, когда показатели
рациональны:

Второе и третье свойства следуют из первого. Четвертое свойство доказывается аналогично первому.


Функцию
 при
при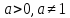 называютпоказательной.При
называютпоказательной.При она возрастающая, а при
она возрастающая, а при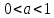 -- убывающая. Функция
-- убывающая. Функция имеет обратную
имеет обратную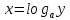 по теореме об обратной функции к
непрерывной монотонной функции. Так мы
приходим к понятию логарифма. Пусть
по теореме об обратной функции к
непрерывной монотонной функции. Так мы
приходим к понятию логарифма. Пусть и
и .
В этом случае
.
В этом случае тогда и только тогда, когда
тогда и только тогда, когда .
Функция
.
Функция называетсялогарифмической. Ее
область определения -- множество
положительных чисел. График логарифмической
функции изображен на рисунке выше.
называетсялогарифмической. Ее
область определения -- множество
положительных чисел. График логарифмической
функции изображен на рисунке выше.
Свойства логарифмической функции следующие
(основное свойство)
 ;
;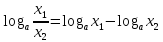 ;
; (здесь
(здесь );
); (здесь
(здесь -- любое ненулевое число);
-- любое ненулевое число); ,
отсюда
,
отсюда и
и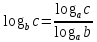 ;
; ;
;если
 ,
то
,
то и
и ;
если же
;
если же ,
то
,
то и
и .
.
Эти
свойства есть следствия свойств
показательной функции. Если
 -- основание натуральных логарифмов, то
полагают
-- основание натуральных логарифмов, то
полагают и называют эту функцию натуральным
логарифмом. Также записывают
и называют эту функцию натуральным
логарифмом. Также записывают и называют эту функцию экспонентой.
и называют эту функцию экспонентой.
