
1167
.pdfзначения εx , εy , γxy из формул закона Гука (80), получаем:
∂2σ |
|
∂2σ |
y |
2 |
|
∂2σy |
|
2 |
|
∂2σ |
|
|
|||||
|
x |
−µ |
|
+ |
∂ σz |
+ |
|
−µ |
∂ σz |
+ |
|
x |
− |
||||
∂y |
2 |
|
|
|
|
2 |
|
∂x2 |
|||||||||
|
|
|
∂y2 ∂y2 |
|
∂x |
∂x2 |
|
||||||||||
|
|
|
|
∂2τxy |
|
|
|
|
|
|
|
|
|
(б) |
|||
−2(1+µ) |
|
= 0. |
|
|
|
|
|
|
|
|
|||||||
|
∂x∂y |
|
|
|
|
|
|
|
|
|
|
||||||
Преобразуем (б), исключив из него касательные напряжения τxy . Для этого продифференцируем первое уравнение равновесия
(статическое) (78) по x, второе – по y, третье – по z. Складывая почленно два первых из полученных уравнений и вычитая третье, находим:
|
|
|
|
−2 |
|
∂2τxy |
|
= |
∂2σ |
x |
+ |
|
∂2σy |
|
− |
∂2σ |
z . |
|
|
|
(в) |
|||||||||||
|
|
|
|
|
∂x∂y |
|
|
|
|
|
∂y2 |
∂z2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂x2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Подставляя полученное решение (в) в уравнение (б), получа- |
||||||||||||||||||||||||||||||||
ем: |
|
|
|
|
|
|
|
∂2σ |
|
|
|
|
∂2σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
∂2σ |
x |
+ |
∂2σ |
x |
|
+ |
y |
|
+ |
|
y |
|
− |
|
∂2σ |
z |
−µ 2σz = 0. |
|
|||||||||||||
|
|
|
∂y2 |
∂x2 |
|
|
|
∂y2 |
|
|
|
|
∂z2 |
|
|
|||||||||||||||||
|
∂x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Прибавим и вычтем в этом уравнении |
∂2σx |
, |
∂2σy |
, |
2 σz . |
|||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
Тогда с учетом уравнения (85) получим |
|
|
|
|
∂z2 |
|
∂z2 |
|
||||||||||||||||||||||||
∂2S1 |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
(1+µ) 2σ |
z |
|
+ |
= 0. |
|
|
|
(г) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z2 |
|
|
|
|
|
|
||||
Аналогично можно преобразовать остальные уравнения не-
разрывности деформаций (53) (или можно сделать круговую подстановку букв x, y, z в уравнении (г)). В результате получим уравнения Бельтрами – Митчела:
(1+µ) 2σx |
|
∂ |
2 |
S1 |
|
|
(1+µ) 2τxy + |
∂ |
2 |
S1 |
|
|
|
|
||||||||||||||
+ |
|
= 0, |
|
= 0, |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
∂x2 |
|
|
|
|
|
|
|
|
|
∂x∂y |
|
|
|
||||||||||
|
|
|
|
|
∂ |
2 |
S1 |
|
|
|
|
|
|
|
|
∂ |
2 |
S1 |
|
|
|
|
|
|||||
(1 |
+µ 2σ |
|
+ |
|
= |
0, |
(1 |
+µ 2τ |
|
+ |
|
|
= |
0, |
|
(86) |
||||||||||||
y |
|
|
|
yz |
|
|
|
|
|
|
||||||||||||||||||
) |
|
|
∂y2 |
|
) |
|
|
|
∂y∂z |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2 |
|
|
|
∂ |
2 |
S1 |
|
|
|
2 |
|
|
|
∂ |
2 |
S1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(1+µ) |
σz |
+ |
|
|
= 0, |
(1+µ) |
τzx |
+ |
∂z∂x |
= |
0. |
|
||||||||||||||||
∂z2 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
71 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эти уравнения получены Бельтрами в 1892 г. В 1899 г. Митчел вывел эти уравнения для случая, когда объемные силы не постоянны, и, следовательно, в правую часть уравнений (86) вместо нулей входят члены, содержащие производные от объемных сил.
Таким образом, для решения задачи теории упругости в напряжениях необходимо проинтегрировать девять уравнений: три равновесия (78) и шесть (86). Наличие трех лишних уравнений необходимо для получения однозначного решения и обсуждалось при выводе уравнений неразрывности деформаций (53), следствием которых являются уравнения Бельтрами-Митчела.
Полученные после интегрирования шесть составляющих напряжений должны удовлетворять условиям на поверхности (8). После этого по формулам закона Гука (80) определяют составляющие деформации, а из формул Коши (79) – составляющие перемещения ux ,uy ,uz .
4.4. Теорема единственности. Методы решения задач теории упругости
При решении задач теории упругости может возникнуть вопрос о том, является ли полученное решение однозначным, т. е. могут ли заданным объемным и поверхностным силам соответствовать одна или несколько различных систем напряжений.
Докажем следующую теорему.
Для тела, находящегося в естественном состоянии, решение задачи теории упругости единственно, если справедлив принцип независимости действия сил.
Предположим обратное: под действием заданных поверхностных pxν, pyν, pzν и объемных X, Y, Z сил возможны две различ-
ные системы напряжений
σ'x , σ'y , σ'z , τ'xy , τ'yz , τ'zx и σ'x' , σ'y' , σ'z' , τ'xy' , τ'yz' , τ'zx' .
Обе эти системы напряжений должны удовлетворять уравнениям статического равновесия (78)
72

∂σ'x + ∂τ'xy
∂x ∂y
∂τ'yx + ∂σ'y ∂x ∂y
∂τ'zx + ∂τ'zy
∂x ∂y
∂σ'x' + ∂τ'xy'
∂x ∂y
∂τ''yx + ∂σ''y ∂x ∂y
∂τ'zx' + ∂τ''zy
∂x ∂y
и условиям на поверхности (8)
+ ∂τ'xz + X =0,
∂z
+∂τ'yz +Y =0, ∂z
+∂σ'z +Z =0, ∂z
+∂τ'xz' + X = 0, ∂z
+∂τ''yz +Y = 0, ∂z
+∂σ'z' + Z = 0, ∂z
(а)
(б)
p |
=σ' l +τ' |
m+τ' |
|
n, |
||
xν |
x |
xy |
xz |
|
||
|
' |
|
' |
' |
|
|
pyν =τyxl +σym+τyzn, |
||||||
p |
' |
' |
' |
|
|
|
=τ l +τ |
zy |
m+σ n, |
||||
zν |
zx |
|
z |
|
|
|
p |
=σ'' l +τ'' |
m+τ'' |
|
n, |
||
xν |
x |
xy |
xz |
|
||
|
'' |
|
'' |
'' |
|
|
pyν =τyxl +σym+τyzn, |
||||||
p |
'' |
'' |
'' |
|
|
|
=τ l +τ |
zy |
m+σ |
n. |
|||
zν |
zx |
|
z |
|
|
|
Вычтя почленно соответствующие уравнения систем (а) и (б), получим новую систему уравнений равновесия:
73
|
∂ |
(σ'x −σ'x' ) + |
|
∂ |
(τ'xy −τ'xy' |
) + |
|
∂ |
|
(τ'xz −τ'xz' |
) = 0, |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
∂x |
∂y |
∂z |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
∂ |
(τ'yx |
−τ'yx' ) + |
∂ |
|
(σ'y −σ'y' |
|
|
∂ |
|
(τ'zy −τ'zy' |
|
|
|||||||
|
|
) + |
|
|
) = 0, |
|||||||||||||||
|
∂x |
∂y |
|
∂z |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
∂ |
(τ'zx |
−τ'zx' ) + |
|
|
∂ |
|
(τ'zy −τ'zy' |
) + |
|
∂ |
|
(σ'z −σ'z' ) = 0 |
|
||||||
|
|
|
|
|
|
|
||||||||||||||
|
∂x |
|
∂y |
|
|
∂z |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
и условий на поверхности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
0 = (σ'x |
−σ'x' )l +(τ'xy −τ'xy' )m +(τ'xz −τ'xz' )n, |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 = (τ'yx −τ'yx' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
)l +(σ'y −σ'y' )m +(τ'yz −τ'yz' )n, |
|
||||||||||||||||||
|
0 = (τ' |
−τ'' |
)l |
+(τ' |
−τ'' )m +(σ' |
−σ'' )n. |
|
|
||||||||||||
|
|
|
||||||||||||||||||
|
|
zx |
zx |
|
|
|
|
|
|
zy |
zy |
|
|
|
|
|
z |
z |
|
|
(в)
(г)
Нa основании принципа независимости действия сил разности напряжений, входящих в системы уравнений (в) и (г), можно принять за новую систему напряжений. Однако согласно уравнениям (в) и (г) полученная новая система напряжений возникает при отсутствии объемных и поверхностных сил. Для тела, находящегося в естественном состоянии, эти напряжения равны нулю, т. е.
' |
'' |
' |
'' |
' |
'' |
|
σx |
−σx |
= 0, τxy − τxy = |
0, τxz − τxz = 0, |
|||
σ' |
−σ'' |
= 0, σ' |
−σ'' = 0, τ' |
− τ'' |
|
|
= 0 |
||||||
y |
y |
z |
z |
yz |
yz |
|
или |
|
|
|
|
|
|
|
σ'x = σ'x' , τ'xy = τ'xy' |
, τ'xz = τ'xz' |
, |
|||
|
σ'y = σ'y' , σ'z = σ'z' , τ'yz = τ'yz' . |
|
||||
Следовательно, обе системы напряжений совпадают, и решение задачи теории упругости, когда заданы объемные и поверхностные силы, единственно.
Точно так же можно доказать единственность решения задачи теории упругости и в случае, когда на поверхности упругого тела заданы перемещения.
Из доказанной теоремы следует, что так как решение задачи
74
теории упругости единственно, то безразлично, каким математическим методом решена задача.
Можно указать три основных метода математического решения задачи теории упругости:
1.Прямой метод. Этот метод заключается в непосредственном интегрировании уравнений теории упругости совместно с заданными условиями на поверхности (54) - (56).
2.Обратный метод. В этом случае задаются функциями перемещений или напряжений, удовлетворяющими дифференциальным уравнениям совместности деформаций или равновесия, и определяют, каким внешним нагрузкам соответствует рассматриваемая система перемещений или напряжений.
3.Полуобратный метод Сен-Венана. Прирешении задачи этим методом делают допущения о виде некоторых из функций напряжений или перемещений. При этом дифференциальные уравнения настолько упрощаются, что решение их не представляет особых трудностей. Полуобратный метод является одним из наиболее эф-
фективных методов решения задачи теории упругости.
Контрольные вопросы
1.Сколько неизвестных функций необходимо определить при решении пространственной задачитеории упругости?
2.Является ли с математической точки зрения разрешимой задача определения компонентов перемещения, напряжений и деформаций?
3.Укажите способы решения задач теории упругости.
4.Как решается задача теории упругости в перемещениях?
5.Синтезом каких уравнений являются уравнения Ламе?
6.Укажите план решения задачи теории упругости в перемещениях.
7.В чемсуть решения задачи теории упругости в напряжениях?
8.Какая функция является гармонической?
9.Описываются ли гармоническими функциями объемная деформация и первый инвариант тензора напряжений?
75

РАЗДЕЛ ВТОРОЙ
ПЛОСКАЯ ЗАДАЧА МАТЕМАТИЧЕСКОЙ ТЕОРИИ УПРУГОСТИ
ГЛАВА 5. ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ
5.1. Плоская деформация
Если при каком-либо напряженном состоянии тела перемещения всех его точек могут происходить только в двух направлениях, т. е. только в одной плоскости, то такая деформация называется плоской. Примером может служить тело, помещенное между двумя абсолютно твердыми плитами (рис. 16), расстояние между которыми остается неизменным, и сжимаемое силами, параллель-
ными плоскостям плит.
В таких же условиях фактически оказывается тело, размеры которого в одном направлении, например в направлении оси z, очень велики (например длинном цилиндрическом катке, длинной пластинке и т. д.).
Если такое длинное в направлении, например, оси z тело нагружено силами (рис. 17), не меняющимися по длине тела и перпендикулярными к этому направлению, то часть его, находящаяся на значительном расстоянии от концов, фактически будет подвергаться плоской деформации.
76
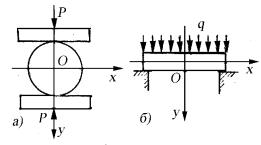
Рис. 17. Плоская деформация при нагружении цилиндрического катка (а) и длинной пластины (б)
пример хОу:
ux = ux (x, y), uy
Перемещения всех точек деформированного тела в таком случае происходят в плоскостях, перпендикулярных к длине тела.
Итак, в упругом теле возникает плоская деформа-
ция, если перемещения будут происходить только параллельно одной плоскости, на-
= uy (x, y), uz = 0. |
(a) |
Подставляя составляющие перемещения (a) в формулы Коши (79), получаем:
εx = εx (x, y), |
εz = 0, |
|
|
εy =εy (x, y), |
γyz = 0, |
|
(б) |
|
|||
γxy = γxy (x, y), |
γzx = 0. |
|
|
|
|
Отсутствие линейных деформаций в направлении оси z ведет к появлению нормальных напряжений σz. Эти напряжения зависят от напряжений, действующих в плоскости xOy. Действительно, из третьей формулы закона Гука (80) при отсутствии деформации εz следует, что
εz = |
1 |
[σz −µ(σx +σy )] = 0, |
|
E |
|
||
откуда |
|
|
|
|
σz = µ(σx + σy ). |
(87) |
|
|
|
Подставляя соотношение (87) в первые две формулы закона Гука (80), находим:
εx
εy
=1−Eµ2
=1−Eµ2
|
|
|
|
|
|
|
µ |
|
|
σ |
x |
− |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
−µ |
||||
|
|
|
|
|||||
|
|
|
|
|
|
|
µ |
|
|
σ |
y |
− |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
−µ |
||||
|
|
|
|
|||||
σ , y
(в)
σ . x
77
Из анализа формул (б), (в) и (80) следует, что τyz = τzx = 0 , а
σx = σx (x, y); σy = σy (x, y); τxy = τxy (x, y).
На основании формулы (87) напряжение σz также является функцией только двух координатσz = σz (x, y) .
Таким образом, основные уравнения теории упругости в случае плоской деформации значительно упрощаются. Из дифференциальных уравнений равновесия (78) остаются только два
∂σ |
x |
|
|
∂τ |
xy |
|
|
|
|
|
|
+ |
|
|
|
+ X = 0, |
|
||||
|
|
|
|
|
|
|||||
∂x |
|
∂y |
|
(88) |
||||||
∂τyx |
|
|
∂σy |
|
|
|||||
+ |
|
+Y = 0, |
|
|
||||||
|
|
|
||||||||
∂x |
|
∂y |
|
|
||||||
|
|
|
||||||||
а третье превращается в тождество.
Так как на боковой поверхности упругого тела везде направляющий косинус n = 0, то из условий на поверхности (8) остаются также только два
p |
xν |
= σ |
l + τ |
xy |
m, |
|
||||
|
|
x |
|
|
|
|
(89) |
|||
p |
|
= τ |
|
|
l +σ |
|
|
|
||
yν |
yx |
y |
m. |
|
||||||
|
|
|
|
|
|
|||||
Формулы Коши (79) сведутся к трем
εx = |
∂ux |
, |
|
|
|
|
|
|
|
||||
|
|
∂x |
|
|
|
|
εy = |
∂uy |
, |
|
|
(90) |
|
|
|
|
|
|||
|
∂y |
|
||||
|
|
|
|
|
|
|
|
|
∂u |
x + |
∂uy |
|
|
γxy = |
|
|
. |
|
||
|
|
|
||||
|
|
∂y |
∂x |
|
|
|
|
|
|
|
|||
Из шести уравнений неразрывности деформаций (53) остается только одно
∂2ε |
x |
+ |
∂2ε |
y |
= |
∂2γ |
xy |
, |
(91) |
|
∂x2 |
|
|
||||||
∂y2 |
|
|
∂x∂y |
|
|||||
а остальные обращаются в тождества.
Из шести формул закона Гука (80) с учетом соотношений (б) и
78
(в) остаются только три
|
|
= 1−µ |
2 |
|
|
|
|
|
|
|
|
µ |
|
||
ε |
x |
|
|
σ |
x |
− |
|
|
|
|
|||||
|
|
|
|
|
|
||||||||||
|
|
|
E |
|
|
|
|
|
1 |
−µ |
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1−µ |
2 |
|
|
|
|
|
|
|
|
µ |
|
|
ε |
y |
= |
|
|
σ |
y |
− |
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||||
|
|
|
E |
|
|
|
|
|
|
1−µ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
γxy = |
2(1+µ) |
τxy. |
|
|
|||||||||||
|
|
|
|||||||||||||
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
σy
σx
,
, (г)
Эти формулы примут более удобный вид, если ввести новые упругие постоянные
E = E (1−µ2 ); |
|
||
1 |
|
(92) |
|
µ1 = µ (1−µ). |
|||
|
|
||
В данном случае выражение коэффициента пропорциональности в третьем уравнении (г) через новые упругие постоянные не изменяется
2(1+µ) E = 2(1+µ1) E1 .
С учетом этого результата и формул (92) формула закона Гука для плоской деформации примет вид
|
|
|
|
|
|
|
|
|
ε |
x |
= (σ |
x |
−µ σ |
) |
E |
; |
|
|
|
1 y |
|
1 |
|
|
||
εy = (σy −µ1σx ) |
E1 |
|
(93) |
|||||
; |
||||||||
γxy = 2(1+µ1) τxy . |
|
|
||||||
|
|
|||||||
|
|
|
|
E1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5.2. Обобщенное плоское напряженное состояние
Все уравнения теории упругости значительно упрощаются, если напряжения параллельны одной плоскости. Так, в задаче о тонкой пластинке, загруженной по боковой поверхности силами, параллельными ее основаниям и равномерно распределенными по ее толщине (рис. 18), возможны упрощения, аналогичные упрощениям в задаче о плоской деформации.
79

|
|
|
Этот |
случай |
называется |
|
|
|
|
||||
|
|
|
обобщенным плоским напряжен- |
|||
|
|
|
ным состоянием. |
|
|
|
|
|
|
На |
основаниях |
пластинки |
|
|
|
|
напряжения σz, τyz и τxz равны ну- |
|||
|
|
|
лю, а так как она тонкая, то мож- |
|||
|
|
|
но считать, что σz = τyz = τxz |
= 0 |
||
|
|
|
по всему объему пластинки. |
По |
||
Рис. 1 8 . Обобщенное плоское |
||||||
напряженное состояние |
той же причине остальные |
на- |
||||
пряжения можно считать постоянными по толщине пластинки, т. е. не зависящими от координаты z. Таким образом, в тонкой пластинке, загруженной силами, параллельными плоскости xOy, возникает напряженное состояние, для которого
σx = σx (x, y); σy = σx (x, y); τxy = τxy (x, y).
Вотношении напряжений обобщенное плоское напряженное
состояние отличается от плоской деформации условием σz = 0. Переходя к деформациям с помощью третьей формулы закона Гука (80), получаем, что деформация
εz = − Eµ (σx +σy ).
Поскольку εz ≠ 0 , то основания пластинки не остаются пло-
скими, а будут искривляться.
При этих предположениях основные уравнения плоской деформации: дифференциальные уравнения равновесия (5), условия на поверхности (8), формулы Коши (44) и уравнение неразрывности деформаций (53) сохранят такой же вид и в задаче об обобщенном плоском напряженном состоянии, а формулы закона Гука (60) примут следующий вид:
εx = (σx −µσy ) E ; εy = (σy −µσx ) E; γxy = 2(1E+µ) τxy .
(94)
Эти формулы отличаются от формул закона Гука для плоской
80
