
1167
.pdfЭтот момент оказывается величиной четвертого порядка малости. Такой же порядок малости имеют моменты массовых сил
Xdxdydz dz2 и Zdxdydz dx2 .
Преобразовав выражение (а) и отбросив величины четвертого порядка малости, после деления на объем рассматриваемого параллелепипеда получим:
τxz = τzx.
Составляя уравнение моментов относительно осей z и x, получаем еще два аналогичных соотношения. Таким образом, из уравнений моментов вытекают три равенства
τxy = τyx; τyz = τzy ; τzx = τxz ,
представляющие собой закон парности касательных напряжений.
Этот закон можно выразить так: в каждых двух взаимно перпендикулярных плоскостях компоненты касательных напряжений, направленные перпендикулярно к линии пересечения этих плоскостей, равны между собой и при этом оба направлены либо к линии пересечения, либо от нее.
Вследствие парности касательных напряжений вместо девяти неизвестных составляющих напряжений, характеризующих напряженное состояние в точке тела, остается только шесть:
σx = σx (x, y, z),
σy = σy (x, y, z),
σz = σz (x, y, z),
τxy = τxy (x, y, z), |
|
|
τyz = τyz (x, y, z), |
|
(6) |
|
||
|
|
|
τzx = τzx (x, y, z). |
|
|
Кроме того, из закона парности касательных напряжений следует, что тензор напряжений (4) – симметричная матрица, так как компоненты, расположенные симметрично относительно главной диагонали, равны между собой ( τij = τji , где i, j = x,y,z ).
Для определения шести неизвестных функций (6) получено только три дифференциальных уравнения равновесия (5).
Следовательно, уравнений статики недостаточно и задача механики деформируемого твердого тела по определению напряжений в бесконечно малом объеме является статически неопредели-
21

мой. Недостающие уравнения можно получить, изучая деформации тела и учитывая его физические свойства в рамках упомянутых выше разделов механики деформируемого твердого тела.
При решении некоторых задач вместо декартовой системы координат удобно пользоваться другими системами, например цилиндрической. В цилиндрической системе координат положение любой точки определяется тремя координатами: x, θ и r, причем две из них x и r – прямолинейные, а третья θ – угловая.
На рис. 5 показан бесконечно малый элемент тела в цилиндрической системе координат и напряжения, действующие на гра-
нях этого элемента.
Из уравнений проекций, действующих на бесконечно малый элемент тела (см. рис. 5) аналогично уравнениям
(5) в декартовой системе координат, получим следующие дифференциальные уравнения равновесия в цилиндрической системе координат:
∂σx
∂x ∂τθx
∂x ∂τrx
∂x
+ 1r ∂∂τθxθ + ∂∂τrxr + τrxr + X =
+1r ∂∂σθθ + ∂∂τrθr + 2τrθr +θ =
+1r ∂∂τθrθ + σr −r σθ + R = 0.
0;
0; (7)
1.4. Напряжения на наклонных площадках. Условия на поверхности
Для исследования напряженного состояния во всех точках упругого тела необходимо уметь находить напряжения в любой площадке, положение которой определяется нормалью ν, направ-
22
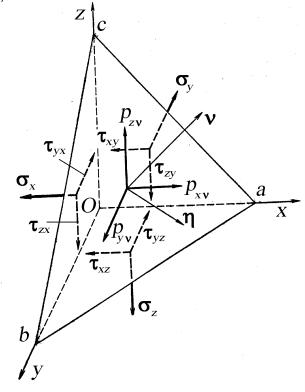
ляющие косинусы которой равны cos(x,ν) = l, cos( y,ν) = m, cos(z,ν) = n (рис. 6). Наклонная площадка abc вместе с коорди-
натными площадками Oab, Obc и Oca образует бесконечно малый тетраэдр. Обозначим площадь наклонной грани abc через dF.
Тогда площади остальных граней тетраэдра, перпендикулярных координатным осям, определим как проекции площади грани abc на соответствующие координатные плоскости: пл. Obc = dF l , пл.
Рис. 6. Площадка с напряжениями на исходных гранях
Oca= dF m ,пл.Oab= dF n.
На рассматриваемый тетраэдр действуют нагрузки: на координатных площадках шесть составляющих напряжений σx,
σy, σz, τxy, τyz и τzx, на пло-
щадке abc три составляющие полного напряжения pxν, pyν, и pzν , а
также по всему объему составляющие объемной силы X, Y, Z (последние на рис. 6 не показаны).
Проектируя на ось x все силы, действующие на тетраэдр Oabc, получаем:
pxνdF −σxdFl −τxydFm −τxzdFn + XdV = 0.
В этом уравнении последнее слагаемое, учитывающее действие объемных сил, имеет третий порядок малости (умножается на объем dV), а остальные – второй (dF). Пренебрегая слагаемыми третьего порядка малости и деля все члены равенства на dF, находим:
pxν = σxl + τxym + τxz n. |
(а) |
Составляя уравнения равновесия всех сил, действующих на
23
тетраэдр Oabc, на оси y и z, получаем еще два уравнения. Таким образом, приходим к следующим трем уравнениям равновесия элементарного тетраэдра:
pxν = σxl + τxy m + τxz n, |
|
|
(8) |
pyν = τyxl + σy m + τyz n, |
|
|
|
pzν = τzxl + τzy m + σz n. |
|
Уравнения (8) позволяют определить составляющие напряжения на любой наклонной площадке с нормалью v с помощью шести составляющих напряжений на площадках, параллельных координатным плоскостям.
Если площадка abc совпадает с поверхностью тела, то составляющие напряжения pxν , pyν и pzν являются составляющими
внешних сил, действующих на поверхности тела. Тогда уравнения
(8) называют условиями на контуре тела, или статическими гра-
ничными условиями, так как они связывают внешние силы с внутренними напряжениями.
В уравнения (8) не входят объемные силы (силы тяжести или инерционные), потому что они являются бесконечно малыми третьего порядка, тогда как все члены уравнения (а) в его первоначальном виде – второго порядка.
Удовлетворение уравнениям (5) и (8) является необходимыми и достаточными для равновесия всего тела под действием заданных внешних сил. Действительно, если составляющие напряжений (6) удовлетворяют уравнениям равновесия (5) во всех точках внутри тела, то все точки внутри тела находятся в равновесии. Если составляющие напряжений (6) удовлетворяют уравнениям (8) в точках у поверхности тела, то все точки тела у поверхности находятся в равновесии. Если же составляющие напряжений (6) одновременно удовлетворяют уравнениям (5) и (8), то все тело в целом находится в равновесии.
И, наоборот, если тело находится в равновесии под действием заданных внешних сил, то во всех точках внутри тела должны обращаться в тождества уравнения (5), а во всех точках у поверхно-
24

сти тела — уравнения (8). Для удобства запоминания условий (8) можно представить их в виде табл. 1.
Таблица 1
Определение поверхностных компонентов внешней нагрузки
Поверхностные |
|
Множители |
|
компоненты |
l |
m |
n |
нагрузки |
|
|
|
pxν |
σx |
τxy |
τxz |
pyν |
τyx |
σy |
τyz |
pzν |
τzx |
τzy |
σz |
Выделенные в табл. 1 компоненты составляют, как известно,
тензор напряжений.
1.5. Исследование напряженного состояния в данной точке тела при известном для нее тензоре напряжений
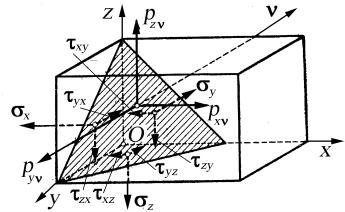
Продолжим исследование напряженного состояния в точке тела. Уравнениями (8) можно воспользоваться для вычисления напряжений в любой точке, расположенной на любой наклонной площадке внутри тела, если известны составляющие напряжений по трем взаимно перпендикулярным площадкам, параллельным координатным плоскостям, или тензор напряжений (4). Действительно, если известны нормальные и касательные напряжения по трем ортогональным граням бесконечно малого параллелепипеда, вырезанного возле данной точки, и требуется определить напряжения в какой-либо наклонной по отношению к граням параллелепипеда (рис. 7), то нужно воспользоваться зависимостью (8). Разница будет лишь в том, что составляющие pxν , pyν и pzν , ко-
торые в (8) были известными внешними силами, в данном случае являются неизвестными составляющими внутренних сил.
Равнодействующая составляющих напряжения на наклонной площадке pxν , pyν и pzν называется полным напряжением на этой
площадке и определяется по формуле
p = |
p2 |
+ p2 |
+ p2 . |
(9) |
ν |
xν |
yν |
zν |
|
|
25 |
|
|
|
Поскольку компоненты pxν , pyν и pzν не являются ни нор-
мальными, ни касательными напряжениями и потому для суждения о прочности не совсем удобны.
Разложим полное напряжение pν на со-
ставляющие по нормали к площадке (это будет нормальное напряжение) и по касательной к последней (это будет касательное напряжение). Итак, нормальное напряжение равно сумме проекций со-
ставляющих pxν , pyν и pzν на направление нормали ν
σν =pxνl + pyνm + pzνn . |
(10) |
Подставляя в (10) значения составляющих pxν , pyν и pzν из
(8), получаем:
σν = σxl2 +σy m2 +σz n2 + 2τxylm + 2τyz mn + 2τzxnl . (11)
Формула (11) позволяет определять нормальные напряжения на любой наклонной площадке с помощью известных компонентов тензора напряжений (4) (шести составляющих напряжений на трех площадках, параллельныхкоординатнымплоскостям(см. рис. 7).
Касательное напряжение на этой площадке определится из уравнения
τ2 |
= p2 |
−σ2 . |
(12) |
ν |
ν |
ν |
|
Последняя формула дает только величину касательного напряжения, но не указывает его направление в плоскости площадки.
Найдем составляющую касательного напряжения в плоскости площадки с нормалью ν по заданному направлению. Для этого зададим в плоскости рассматриваемой площадки с нормалью ν (см. рис. 6) направление η с направляющими косинусами l1, m1, n1 . Так
26
как направления ν и η взаимно перпендикулярны, то между их направляющими косинусами существует известное соотношение
ll1 + mm1 + nn1 = 0. |
(13) |
Касательное напряжение на площадке с нормалью ν в направ- |
|
лении η равно |
сумме проекций составляющих полного напряже- |
|
ния pxν , pyν и |
pzν на этой площадке на направление η: |
|
την = σxll1 +σy mm1 +σz nn1 + τxy (lm1 |
+l1m) + |
|
+ τyz (mn1 + m1n) + τzx (nl1 + n1l). |
(14) |
|
|
||
Формула (14) позволяет определить касательные напряжения на любой наклонной площадке в заданном направлении с помощью шести составляющих напряжений по трем площадкам, параллельным координатным плоскостям.
1.6. Главные напряжения
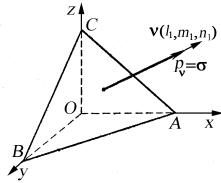
Если положение наклонной площадки (см. рис. 7) менять в пространстве, то при определенных значениях направляющих косинусов l1, m1, n1 полный вектор напряжений pν будет совпадать с
нормалью ν к наклонной площадке (рис. 8). В этом случае в наклонной площадке ABC будет отсутствовать проекция полного вектора напряжений pν на эту площадку, т. е. на ABC не будет
касательных напряжений.
|
|
Площадка, на которой касатель- |
|
|
|
||
|
|
ные напряжения равны нулю, называ- |
|
|
|
ется главной, а нормальное напряже- |
|
|
|
ние – главным напряжением. |
τν = 0 , |
|
|
В этом случае (см. рис. 8) |
|
|
|
а pν = σ. В данном случае σ – искомое |
|
|
|
главное напряжение. Проектируя его |
|
|
|
на координатные оси, находим состав- |
|
Рис. 8. Положение главной |
|||
площадки |
ляющие главного напряжения, |
парал- |
|
лельные координатным осям: |
(а) |
||
|
σl1 = pxν; σm1 = pyν; σn1 = pzν. |
||
|
|
27 |
|
Сравнивая соотношение (а) и (8), получаем: |
|
|||||
σl1 = σxl1 + τxy m1 + τxz n1, |
|
|
||||
|
|
|||||
σm1 = τyxl1 + σy m1 + τyz n1 |
, |
(15) |
||||
σn = τ |
l + τ |
m |
+ σ |
n . |
|
|
1 |
zx 1 |
zy 1 |
z |
1 |
|
|
Кроме того, имеем известное из аналитической геометрии соотношение между направляющими косинусами
l2 |
+ m2 |
+ n2 |
=1. |
(16) |
1 |
1 |
1 |
|
|
Уравнения (15) и (16) содержат четыре неизвестных: главное напряжение σ1 и три его направляющих косинуса.
Представим уравнение (15) в виде
(σx −σ)l1 + τxy m1 |
+ τxz n1 |
= 0, |
|
|
||||
|
|
|
|
|
|
|
|
(17) |
τyxl1 +(σy −σ)m1 + τyz n1 = 0, |
||||||||
τ |
l + τ |
m |
+(σ |
z |
−σ)n |
= 0. |
|
|
|
zx 1 |
zy 1 |
|
1 |
|
|
|
|
Система (17) – система трех линейных однородных алгебраических уравнений не допускает тривиального решения l1 =m1 =n1 = 0 в силу соотношения (16). Для того чтобы однород-
ная система (17) имела решения, отличные от нулевого, необходимо и достаточно, чтобы определитель этой системы был равен нулю, т. е.:
|
σx −σ |
τxy |
τxz |
|
(б) |
∆ = |
τyx |
σy −σ |
τyz |
=0. |
|
|
τzx |
τzy |
σz −σ |
|
|
Раскроем определитель (б)
(σx −σ)(σy −σ)(σz −σ) + τxyτyz τzx + τyxτzy τzx − −(σy −σ)τ2xz −(σx −σ)τ2yz −(σz −σ)τ2xy = 0.
После перемножения и группировки по степеням σ получим кубическое уравнение
σ3 −(σx +σy +σz )σ2 +(σxσy +σyσz +σzσx −τ2xy −τ2yz − (18) −τ2zx )σ−(σxσyσz + 2τxyτyzτzx −σxτ2yz − σy τ2zx −σz τ2xy ) = 0.
28
Полученное кубическое уравнение имеет три корня, которые
идают величины главных напряжений. Как известно, кубическое уравнение имеет либо три действительных корня, либо один корень действительный, а два – комплексно-сопряженных.
Докажем, что все три корня полученного кубического уравнения являются действительными величинами, следовательно, в каждой точке упругого тела существуют три главных напряжения
итри главных площадки, в которых они действуют [6]. Обозначим главные напряжения через
σ1 > σ2 > σ3 ,
где σ1 – наибольшее, а σ3 – наименьшее (в алгебраическом смысле)
главные напряжения, а направляющие косинусы нормалей к главным площадкам, в которых действуют главные напряжения соответственно через l1, m1, n1 – для площадки с напряжением σ1, l2 , m2 , n2 –
для площадки с напряжением σ2, l3 , m3 , n3 – для площадки с на-
пряжением σ3.
Для доказательства подставим значение главного напряжения σ1 и направляющих косинусов l1, m1 и n1 в уравнение (17).
В результате получим
(σx −σ1)l1 + τxym1 + τxz n1 = 0, |
|
|||||
τyxl1 + (σy −σ1)m1 + τyz n1 = 0, |
(19) |
|||||
τ |
l + τ |
m + (σ |
z |
−σ )n |
= 0. |
|
|
zx 1 |
zy 1 |
1 1 |
|
|
|
Умножая далее каждое из уравнений (19) соответственно на l2 , m2 , n2 и складывая почленно, получаем:
[(σx −σ1)l1 + τxym1 + τxz n1]l2 |
|
+[τyxl1 +[(σy −σ1)m1 |
+ |
|||||||||
+ τyz n1]m2 + +[τzxl1 + τzy m1 + |
(σz −σ1)n1]n2 = 0. |
(20) |
||||||||||
|
||||||||||||
Подставляя σ2 и направляющие косинусы для второй главной площадки |
||||||||||||
l2 , m2 , n2 (вместо l1, m1, n1 ) в уравнение (17), получаем: |
|
|
||||||||||
(σx −σ2 )l2 + τxym2 + τxz n2 = 0, |
|
|||||||||||
τyxl2 +(σy −σ2 )m2 + τyz n2 = 0, |
(21) |
|||||||||||
τ |
l |
2 |
+ τ |
m |
+(σ |
z |
−σ |
2 |
)n |
= 0. |
|
|
|
zx |
|
zy 2 |
|
|
|
2 |
|
|
|||
|
|
|
|
|
29 |
|
|
|
|
|
|
|
Умножая каждое из уравнений (21) соответственно на l1, m1, n1 и складывая их, имеем:
[(σx −σ2 )l2 + τxym2 + τxz n2 ]l1 +[τyxl2 +[(σy −σ1)m2 +
(22)
+ τyz n2 ]m1+ +[τzxl2 + τzym2 +(σz −σ1)n2 ]n1 = 0.
Вычитая из уравнения (20) уравнение (22), получим после преобразований:
(σ2 −σ1)(l1l2 + m1m2 + n1n2 ) = 0. |
|
Так как в общем случае σ1 ≠ σ2 , |
|
то |
|
l1l2 + m1m2 + n1n2 = 0. |
(23) |
Если предположить, что два корня σ1 и σ2 являются комплексносопряженными величинами, т. е.
σ1 = a +bi и σ2 = a −bi ,
то на основании системы уравнений (17) должны быть комплексносопряженными направляющие косинусы l1 и l2, m1 и m1, n1 и n2, а следовательно,
l1l2 > 0, m1m2 > 0, n1n2 > 0.
В таком случае левая часть уравнения (23) не может быть равна нулю. Таким образом, предположение о том, что величины σ1 и σ2 являются ком-
плексно-сопряженными, не соответствует действительности. Аналогичное доказательно можно провести для любой пары главных напряжений σ1, σ2 и σ3.
Следовательно, все три корня σ1, σ2 и σ3 кубического уравнения (18) являются действительными величинами и в любой точке упругого тела существуют:
•три главных напряжения σ1, σ2 и σ3;
•три главные площадки с нормалями ν1, ν2 и ν3, определяемые соответственно направляющими косинусами l1, m1, n1 , l2 , m2 , n2
и l3 , m3 , n3 .
Так как уравнение (23) представляет собой условие перпендикулярности нормалей ν1 и ν2, то отсюда следует, что две главные площадки, в которых имеются напряжения σ1 и σ2, взаимно перпендикулярны. Аналогично можно доказать, что
l1l3 + m1m3 + n1n3 = 0,
т. е. нормали ν1 и ν3, а следовательно, и главные площадки с напряжениями σ1 и σ3 также взаимно перпендикулярны.
Таким образом, все три нормали ν1, ν2 и ν3 к главным площадкам взаимно перпендикулярны. Итак, в каждой точке упругого те-
30
