
1167
.pdf
σx = |
∂W |
, |
σy = |
∂W |
, |
σz = |
∂W |
, |
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||
∂εx |
∂εy |
∂εz |
|
||||||||||||
|
|
|
|
|
|
|
|
(72) |
|||||||
|
|
∂W |
|
|
|
|
∂W |
|
|
∂W |
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
τxy = |
|
|
|
|
|
, τyz = |
|
|
, τzx = |
|
|
. |
|
||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
∂γxy |
|
|
∂γyz |
|
|
∂γzx |
|
|
|||||
|
|
|
|
|
|
|
|
||||||||
Таким образом, составляющие напряжений выражаются через частные производные от удельной потенциальной энергии (в) по соответствующим им составляющим деформации. Эти формулы выведены впервые Грином. Функция W называется упругим потенциа-
лом.
Сопоставляя формулы (67) и (72), заключаем, что частные производные функции W по составляющим деформации представляют собой однородные линейные функции составляющих деформаций εx , εy , εz , γxy , γyz , γzx , следовательно, сама функция W является
однородной функцией второй степени этих составляющих. Вид функции W можно получить с помощью теоремы Эйлера об однородных функциях, которая утверждает, что если F(x, у, z, ...) есть однородная функция n-й степени, то
∂∂Fx x + ∂∂Fy y + ∂∂Fz z +... = nF.
Применив теорему Эйлера к функции W, найдем:
∂W |
εx + |
∂W |
εy + |
∂W |
εz + |
∂W |
γxy + |
∂W |
γyz + |
∂W |
γzx = 2W. |
|||||||
∂ε |
x |
∂ε |
y |
∂ε |
z |
∂γ |
xy |
∂γ |
yz |
∂γ |
zx |
|||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Заменив здесь частные производные упругого потенциала W напряжениями, согласно формулам (72) получим:
W = |
1 |
(σxεx + σyεy + σzεz + τxy γxy + τyz γyz + τzx γzx ). |
(73) |
|
2 |
|
|
Следовательно, удельная потенциальная энергия, накапливаемая в упругом теле, равна половине суммы произведений составляющих напряжений на соответствующие им составляющие деформа-
ции. Это соотношениеназывают формулой Клапейрона.
Формулу Клапейрона можно выразить через одни составляющие напряжений или только через составляющие деформации. Подставляя в зависимость (73) формулы закона Гука в виде (61),
61
находим выражение удельной потенциальной энергии через напряжения:
W = |
1 |
[σ2x + σ2y + σ2z |
− 2µ(σxσy + σyσz + σzσx ) + |
|
|
2E |
(74) |
||||
|
|
|
+ 2(1+µ)(τ2xy + τ2yz + τ2zx )].
Подставляя в зависимость (73) выражение закона Гука в форме (67), получаем выражение удельной потенциальной энергии через деформации:
W = |
1 |
[λθ2 |
+ 2G(ε2x +ε2y +ε2z ) +G(γ2xy + γ2yz + γ2zx )]. |
(75) |
|
2 |
|
|
|
В формуле (75) упругие постоянные Ламе λ и G в соответствии с формулой (66) – величины положительные, следовательно, потенциальная энергия W всегда является величиной положитель-
ной, т. е. W > 0.
Потенциальную энергию, накапливаемую во всем теле, подсчитываем суммированием удельной потенциальной энергии по всему объему тела V:
U = ∫∫∫Wdxdydz. |
(76) |
V |
|
Подставляя в (76) выражение потенциальной энергии из формулы Клапейрона (73), получаем:
U = |
1 |
∫∫∫(σxεx + σyεy + σzεz + τxy γxy + τyz γyz + τzx γzx )dxdydz. (77) |
|
2 |
V |
Соотношение (77) позволяет подсчитать потенциальную энергию, накапливаемую в упругом теле в процессе деформации.
Контрольные вопросы
1.Сформулируйте обобщенный закон Гука.
2.Какая связь между модулем сдвига G и модулем упругости E?
3.Что такое модуль объемного расширения?
4.Как определяются коэффициенты Ламе?
5.Сформулируйте обратную форму закона Гука.
6.Чему пропорционально среднее напряжение в окрестности данной точки упругого тела?
7.Что называется упругим потенциалом?
8.Какая связь между удельной потенциальной энергией и составляющими тензора напряжений?
62
ГЛАВА 4. О РЕШЕНИИ ЗАДАЧ ТЕОРИИ УПРУГОСТИ
4.1. Основные уравнения теории упругости и способы их решения
Рассмотренные ранее уравнения теории упругости распределим в три группы.
А. Группа статических или динамических уравнений.
В эту группу входят дифференциальные уравнения равновесия (5). Для динамической задачи, принимая, что перемещения ux ,uy ,uz очень малые, а проекции ускорения на координатные оси
запишутся как ∂2ux 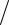 ∂t2 , ∂2uy
∂t2 , ∂2uy 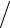 ∂t2 , ∂2uz
∂t2 , ∂2uz 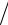 ∂t2 , удельная объемная сила по осям x, y, z будет равна:
∂t2 , удельная объемная сила по осям x, y, z будет равна:
−ρ |
∂2u |
x , |
−ρ |
∂2uy |
, |
−ρ |
∂2u |
z . |
(а) |
|
∂t2 |
∂t2 |
|||||||
|
∂t2 |
|
|
|
|
|
|||
В случае динамической задачи уравнения (5) будут содержать, кроме объемных (массовых) сил X, Y, Z, отнесенных к единице объема, и инерционные силы, определяемые в соответствии с (а).
Система уравнений будет иметь вид
|
∂σx |
+ |
|
∂τ |
xy |
+ |
|
|
∂τxz |
+ X = 0 (или |
ρ |
∂ |
2 |
ux |
); |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
∂y |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
∂x |
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t 2 |
|
|
|
|
||||||||
|
∂τ yx |
|
|
|
∂σ y |
|
|
|
|
∂τ yz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
2 |
uy |
|
|
|
|
||||||||
|
+ |
|
|
+ |
|
|
+Y |
= 0 |
|
(или |
ρ |
|
); |
|
(78) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
∂x |
|
|
∂y |
|
|
|
∂z |
|
|
∂t 2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
∂τ |
zx |
|
|
|
|
∂τ |
zy |
|
|
|
|
∂σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂2u |
y |
|
|
|
||||
|
|
|
+ |
|
|
|
+ |
|
|
|
|
z |
+ Z |
= 0 |
|
|
|
(или ρ |
|
|
|
|
). |
|
|||||||||||||||
|
∂x |
|
|
∂y |
|
|
|
∂z |
|
|
|
∂t 2 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Б. Геометрические уравнения (44) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
εx = |
|
∂u |
x |
; |
γxy = |
∂u |
x |
+ |
∂uy |
; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
εy = |
|
∂uy |
|
; |
|
γyz = |
|
∂uy |
+ |
|
∂u |
z ; |
|
|
|
|
|
|
|
|
|
(79) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
∂y |
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
ε |
|
|
= |
|
∂u |
z |
; |
|
γ |
|
= |
|
∂u |
z |
|
+ |
|
∂u |
x |
. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
z |
|
|
|
|
zx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
∂z |
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
63 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В. Физические уравнения (60)
|
|
1 |
|
[σx −µ(σy +σz )], γxy = |
|
τ |
xy |
|
|
|
||||
εx = |
|
|
|
|
, |
|||||||||
E |
|
G |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
εy = |
1 |
|
[σy −µ(σz +σx )], |
γyz = |
|
τyz |
, |
|||||||
E |
|
|
|
|||||||||||
|
|
|
[σz −µ(σx +σy )], |
|
|
|
|
G |
|
|
|
|||
|
|
1 |
|
|
|
|
τ |
zx |
|
|
||||
εz = |
|
|
|
γzx = |
|
|
|
, |
||||||
|
E |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
G |
|||||
или в обратной форме (67) |
|
|
|
|
|
|
|
|
|
|
||||
σx = λθ+ 2Gεx , |
τxy |
= Gγxy , |
|
|
|
|||||||||
σy = λθ+ 2Gεy , |
τyz |
|
|
|
|
|
|
|
|
|||||
= Gγyz , |
|
|
|
|||||||||||
σz = λθ+ 2Gεz , |
τzx = Gγzx. |
|
|
|
|
|||||||||
|
|
|
|
|||||||||||
(80)
(80а)
Уравнения (78) - (80) (их количество 15) содержат 15 неизвестных функций: шесть компонентов напряжений
σx (x, y, z), σy (x, y, z), σz (x, y, z),
τxy (x, y, z), τyz (x, y, z), τzx (x, y, z),
шесть компонентов деформации
εx (x, y, z), εy (x, y, z), εz (x, y, z),
γxy (x, y, z), γ yz (x, y, z), γzx (x, y, z),
атакже три компонента перемещения
ux (x, y, z), uy (x, y, z), uz (x, y, z) .
Таким образом, с математической точки зрения задача может быть разрешена и сводится к нахождению 15 функций, удовлетворяющим уравнениям (78), (79), (80) или (80а), а также условиям на контуре (8):
pxν = σxl + τxy m + τxz n, |
|
|
(б) |
pyν = τyxl + σy m + τyz n, |
|
|
|
pzν = τzxl + τzy m + σz n. |
|
К ним необходимо присоединить уравнения неразрывности деформаций (53)
64
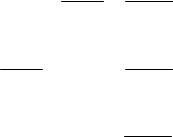
∂∂2ε2x + ∂∂2ε2y = ∂2γxy , y x ∂x∂y
∂2εy + ∂2εz = ∂2γyz , ∂z2 ∂y2 ∂y∂z
∂2εz + ∂2εx = ∂2γzx ; ∂x2 ∂z2 ∂z∂x
|
∂ |
|
|
|
∂γzx |
+ |
∂γ |
xy |
|||
|
|
|
|
|
|
||||||
|
|
|
|
|
∂y |
|
|
|
∂z |
||
∂x |
|
|
|
|
|||||||
|
∂ |
|
|
∂γ |
xy |
|
|
∂γ |
yz |
||
|
|
|
|
|
+ |
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
∂z |
|
|
|
∂x |
||
∂y |
|
|
|
|
|||||||
|
∂ |
|
|
|
∂γ |
yz |
|
|
|
∂γzx |
|
|
|
|
|
|
|
+ |
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
∂x |
|
|
|
∂y |
||
|
∂z |
|
|
|
|
||||||
|
∂γ |
|
|
|
|
|
|
∂ |
2 |
εx |
|
− |
|
yz |
= 2 |
|
|
, |
|||||
∂x |
|
|
|
∂y∂z |
|||||||
|
|
|
|
|
|
||||||
|
∂γ |
|
|
|
|
|
∂2εy |
|
|||
|
zx |
|
|
|
|
||||||
− |
|
|
|
= 2 |
|
|
|
|
, (в) |
||
|
|
|
|
|
|
||||||
∂y |
|
|
|
∂z∂x |
|||||||
|
|
|
|
|
|
||||||
|
∂γ |
|
|
|
|
|
|
|
2 |
|
|
|
xy |
|
|
∂ εz |
|
||||||
− |
|
|
= 2 |
|
|||||||
|
|
|
|
|
|
|
|
|
. |
||
|
∂z |
|
|
|
|
∂x∂y |
|
||||
|
|
|
|
|
|||||||
При прямом решении задачи, когда используются все 15 уравнений (78) - (80), уравнения неразрывности (в) сами по себе, как вытекающие из (79), не нужны и могут выполнять роль контрольных уравнений.
Однако, если решается статическая задача теории упругости (следовательно, правая часть уравнений (78) обращается в нуль) и отыскиваются только напряжения и деформации (значит, неизвестных будет 12), целесообразно уравнения (79) подменить тремя из шести уравнениями (в) или принять первую группу уравнений неразрывности. В этом случае будем иметь три уравнения равновесия (78), шесть физических уравнений (80) и три уравнения неразрывности (в) (для линейных деформаций). Задача сводится к нахождению 12 неизвестных функций, удовлетворяющих в каждой точке упругого тела 12 уравнениям, а на поверхности тела удовлетворяющих граничным уравнениям (б).
Далее, если это потребуется, по найденным деформациям из (80) можно вычислить компоненты перемещений ux (x, y, z),
ux (x, y, z), uy (x, y, z), uz (x, y, z) .
Решение указанных уравнений можно вести различными способами в зависимости от того, какие величины приняты за основные неизвестные:
1. Решение в перемещениях, когда за основные неизвестные приняты три составляющие перемещения:
ux (x, y, z), uy (x, y, z), uz (x, y, z) .
Этот метод часто называют методом перемещений [5]. При
65
решении задачи используются кинематические граничные условия или граничные условия смешанного типа.
2. Решение в напряжениях, когда за основные неизвестные приняты шесть составляющих напряжений
σx (x, y, z), σy (x, y, z), σz (x, y, z), τxy (x, y, z), τyz (x, y, z), τzx (x, y, z).
Этот метод часто называют методом сил [5]. При решении задачи используются статические или динамические граничные условия.
3. Решение в смешанной форме, когда за основные неизвестные приняты некоторые из перемещений и некоторые из напряжений. При решении задачи используются граничные условия смешанного типа.
4.2. Решение задачи теории упругости в перемещениях
При решении задачи теории упругости в перемещениях за основные неизвестные принимают три составляющие перемещения
ux (x, y, z), uy (x, y, z), uz (x, y, z) .
Для их отыскания необходимо иметь три уравнения, которые можно получить из дифференциальных уравнений равновесия (78)
(в статической форме, т. е. ∂2ui 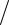 ∂t2 = 0, i = x, y, z ), выразив в них
∂t2 = 0, i = x, y, z ), выразив в них
напряжения через перемещения.
Возьмем первое уравнение равновесия (5) и подставим в него напряжения из формул закона Гука в форме (80а) (обратная форма закона Гука): σx , τxy , τxz . Дифференцируя их в соответствии с
(80а), получим:
∂σ |
x |
= G |
∂2u |
x |
+G |
∂2u |
x + λ |
∂θ |
, |
∂τxy |
= G |
∂2uy |
+G |
∂2u |
x , |
||
|
|
|
|
∂x |
∂y |
∂x∂y |
|
||||||||||
∂x |
|
∂x2 |
|
|
∂x2 |
|
|
|
∂y2 |
||||||||
∂τ |
xz |
= G |
∂2u |
z |
+G |
∂2u |
x . |
|
|
|
|
|
|
|
|
||
∂z |
|
∂x∂z |
|
∂z2 |
|
|
|
|
|
|
|
|
|||||
Внесем полученные решения в первое уравнение группы (78). После группировки находим
66

|
∂θ |
|
|
|
|
∂ |
2u |
|
|
|
|
∂ |
2uy |
|
|
∂2u |
|
|
||||||||
λ |
|
+G |
|
|
|
|
|
x |
+ |
|
|
|
|
|
|
+ |
|
|
z |
+ |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
∂x |
|
|
|
|
∂x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
∂x∂y ∂x∂z |
(а) |
||||||||||||||
|
|
∂ |
2 |
ux |
|
|
|
∂ |
2 |
ux |
|
|
|
∂ |
2 |
ux |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
+ |
|
|
|
|
+ |
|
|
|
|
+ X = 0. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
+G |
∂x |
2 |
|
|
∂y |
2 |
|
|
∂z |
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Выражение, заключенное в первой скобке, может быть короче записано так:
∂2u |
|
∂2uy |
|
∂2u |
|
|
∂ |
|
∂u |
|
∂uy |
|
∂u |
|
|
|
|
|
|
x + |
|
+ |
|
z |
= |
|
|
|
x + |
|
+ |
|
z |
= |
|
|
|
|
|
|
|
|
|
||||||||||
∂x |
2 |
∂x∂y |
|
|
|
|
|
|
∂x |
∂y |
|
∂z |
|
|
|||
|
|
|
∂x∂z ∂x |
|
|
|
|||||||||||
= ∂∂x (εx +εy +εz ) = ∂∂θx .
Введем для краткости письма обозначение
∂2ux |
+ |
∂2ux |
+ |
∂2ux |
= 2ux |
(81) |
|
|
∂z2 |
||||
∂x2 |
∂y2 |
|
|
|||
(читается «набла два»), называемое также оператором Лапласа над функцией ux (x, y, z). Тогда уравнение (а) после группировки по-
добных членов будет иметь вид
(λ +G) |
∂θ |
+G 2ux + X = 0. |
(б) |
|
∂x |
|
|
Аналогично преобразуем и два других дифференциальных уравнения равновесия (78)11. Таким образом, получаем группу уравнений для решения задачи теории упругости в перемещениях
(λ +G) |
∂θ |
|
|
|
∂x |
+G 2ux + X = 0, |
|
||
|
|
|
|
|
(λ +G) |
∂θ |
+G 2uy +Y = 0, |
|
(82) |
∂y |
|
|||
|
|
|
|
|
(λ +G) |
∂θ |
+G 2uz + Z = 0. |
|
|
|
|
|||
|
∂z |
|
|
|
Уравнения (82) называются уравнениями Ламе. Они объеди-
11 Можно и сразу написать результат, сделав в (б) круговую подстановку букв x, y, z.
67
няют все три группы уравнений (78) - (80). Действительно, они содержат условия равновесия, геометрические характеристики деформаций, ux (x, y, z), uy (x, y, z), uz (x, y, z) и физические характе-
ристики материала λ и G.
Поверхностные условия (8) также можно преобразовать, выразив напряжения через перемещения. Для этого подставим в первое уравнение (8) (или (б) п. 4.1) на место напряжений σx , τxy , τxz
выражение для них в форме (80а). Получим |
|
pxν = (λθl + 2Gεx )l +Gγxym +Gλxzn. |
(в) |
Подставим в (в) вместо линейных и угловых деформаций их значения из формул Коши (79) и сгруппируем следующим образом:
|
∂u |
x |
|
∂u |
x |
|
∂u |
x |
|
|
∂u |
x |
|
∂uy |
|
∂u |
z |
|
|
|
l + |
|
m + |
|
|
|
|
l + |
|
m + |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
pxν = λθl +G |
∂x |
∂y |
∂z |
n |
+G |
∂x |
∂x |
∂x |
n . |
|||||||||
|
|
|
|
|
|
|
|
|||||||||||
(г)
Выражение в первой скобке уравнения (г) представляет собой производную по направлению нормали ν от функции ux (x, y, z) [10]. Действительно, вычисляя частную производную сложной
функции ux (x, y, z) |
по ν, получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
∂ux |
= |
∂ux |
|
dx + |
|
∂ux |
|
dy |
+ |
∂ux |
|
dz . |
|
||||||||||||||
|
∂ν |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
∂x dν ∂y dν ∂z dν |
|
||||||||||||||||||||||||
Производные координат по ν представляют собой соответст- |
||||||||||||||||||||||||||||
вующие направляющие косинусы нормали ν |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
dx |
= l, dy |
= m, |
dz |
= n. |
|
|
|
|||||||||||||||||
|
|
|
|
dν |
|
|
dν |
|
|
|
|
|
dν |
|
|
|
|
|
|
|||||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
∂ux |
|
|
|
|
∂ux |
|
|
|
|
|||||||||
|
|
|
|
∂ux |
= |
|
∂ux |
l + |
m + |
n |
|
|
||||||||||||||||
|
|
|
|
∂ν |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
∂x |
|
|
∂y |
|
|
|
|
|
∂z |
|
|
|
|
|||||||||
и формула (г) принимает следующий вид: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
∂ux |
|
|
|
|
|
|
|
|
∂u |
y |
|
|
|
∂uz |
|
||||||||
pxν = λθl +G |
|
|
|
∂ux |
l + |
|
|
m + |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
∂ν |
+G |
∂x |
∂x |
|
∂x |
n . |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Точно так же можно преобразовать два других уравнения из
68
условий на поверхности (8). В результате приходим к следующим трем условиям на поверхности, выраженным через перемещения:
pxν
pyν
pzν
|
∂ux |
|
|
|
∂ux |
|
|
∂u |
y |
|
|
|
|
∂uz |
|
|
|
|
|
|||||||||||
= λθl +G |
|
|
|
l + |
|
|
|
|
|
m + |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
∂ν |
+G |
∂x |
|
|
∂x |
|
|
∂x |
n , |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
∂u |
y |
|
|
∂ux |
|
|
|
|
∂u |
y |
|
|
|
|
∂uz |
|
|
|
|
||||||||
= λθm +G |
|
|
|
|
|
l + |
|
|
|
|
m + |
|
|
|
|
(83) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
∂ν |
|
+G |
∂y |
|
|
∂y |
|
|
|
∂y |
|
|
n , |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
∂u |
|
|
|
|
∂u |
|
|
|
|
∂uy |
|
|
|
|
∂u |
|
|
|
|
|
|
||||||||
= λθn +G |
|
|
|
z |
|
|
|
|
|
x |
l + |
|
|
|
|
|
|
|
m + |
|
|
|
z |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
∂ν |
|
+G |
|
∂z |
|
|
|
∂z |
|
|
|
∂z |
|
n . |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Составим план решения задачи теории упругости в переме-
щениях. Для определения |
трех составляющих перемещения |
ux (x, y, z), uy (x, y, z), uz (x, y, z) |
необходимо проинтегрировать три |
уравнения Ламе (82) и удовлетворить условиям на поверхности (83). По найденным перемещениям из формул Коши (79) определяют составляющие деформаций, а затем из формул закона Гука (80а) – составляющие напряжений.
Заметим, что для динамической задачи правая часть уравне-
ний (82) равна ρ ∂2ui ( ui = x, y, z ).
∂t2
4.3. Решение задачи теории упругости в напряжениях при постоянстве объемных сил
Ограничим круг рассматриваемых задач случаями статического равновесия, когда объемные силы постоянны по всему объему тела или равны нулю. Эти ограничения позволяют значительно упростить некоторые уравнения при решении задач в напряжениях, так как все производные от составляющих объемных сил по координатам x, y, z обращаются в нуль.
Рассмотрим свойства функций θ и S1 при постоянстве объемных сил.
Продифференцируем первое уравнение Ламе из зависимости (82) по x, второе – по y, третье – по z и сложим почленно. В результате получим
69
|
|
∂2θ ∂2θ ∂2 |
θ |
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
∂ |
|
|
|
|
||||||||||||
|
|
|
2 + |
|
|
|
|
+ |
|
|
|
|
|
|
|
2 |
ux |
|
|
|
|
|
|
|
2 |
uy |
|
|
|
|
2 |
|
|
|||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
|
|||||||||||||||||
(λ +G) |
∂x |
∂y |
∂z |
2 |
+G |
∂x |
|
∂y |
∂z |
uz = 0. (а) |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Выражение, стоящее в первых скобках, представляет собой |
||||||||||||||||||||||||||||||||||||||||
оператор Лапласа над функцией θ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂2θ |
+ |
∂ |
2θ |
+ |
∂2θ |
|
= 2θ. |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x2 |
∂y2 |
|
∂z2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Вторые скобки преобразуем следующим образом: |
|
|
||||||||||||||||||||||||||||||||||||||
∂ 2 |
|
|
∂ 2 |
|
|
|
∂ 2 |
|
|
|
|
|
2 |
|
|
∂u |
x |
|
|
∂uy |
|
|
∂u |
z |
|
2 |
|
|||||||||||||
|
|
ux + |
|
|
|
uy |
+ |
|
|
uz |
= |
|
|
|
|
|
|
|
|
+ |
|
|
+ |
|
|
|
|
= θ. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
∂x |
∂y |
∂z |
|
|
|
|
∂x |
∂y |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
|||||||||||||||||
Тогда вместо уравнения (а) получим |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(λ + 2G) 2θ = 0, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2θ = 0. |
|
|
|
|
|
|
|
|
|
|
(84) |
|||||||||||
Функция, подчиняющаяся условию (84), называется гармони- |
||||||||||||||||||||||||||||||||||||||||
ческой функцией. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Следовательно, при постоянстве объемных сил объемная де- |
||||||||||||||||||||||||||||||||||||||||
формация есть функция гармоническая. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Подставляя формулу (62) для объемной деформации θ в урав- |
||||||||||||||||||||||||||||||||||||||||
нение (84), получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2S |
|
= 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(85) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т. е. при постоянстве объемных сил первый инвариант напряженного состояния есть функция гармоническая.
При решении задачи теории упругости в напряжениях за основные неизвестные принимают шесть составляющих напряжений: σx , σy , σz , τxy , τyz , τzx . Для их отыскания трех уравнений
равновесия (78) недостаточно и поэтому к ним нужно добавить еще шесть уравнений неразрывности деформаций (53). Так как в последние входят составляющие деформации, то их необходимо предварительно выразить через напряжения.
Подставляя в первое уравнение неразрывности деформаций
∂2ε |
x |
+ |
∂2ε |
y |
= |
∂γ |
xy |
∂y2 |
|
∂x2 |
|
∂x∂y |
|||
|
|
|
70 |
|
|
|
|
