§5. Правила математической обработки результатов эксперимента

15.1. Прямые измерения

1. Результаты измерений записать в таблицу.

2. Вычислить выборочное среднее из N измерений:

(5.1.1)

3. Если какой-либо результат измерения резко отличается по своему значению от остальных, то следует проверить не обусловлен ли он промахом по процедуре, изложенной в §3.5. Если это так, то данный результат нужно отбросить и повторить расчет по формуле (5.1.1).

4. Вычислить выборочноё стандартное отклонение среднего:

(5.1.2)

5. Определить различные составляющие погрешностей средств измерений для вероятности 68%. Среди них:

Δ_п – ошибка прибора; если ошибка прибора задается как предельная (максимальная) Δ_пр, то для α=68%

Δ_п ; (5.1.3.)

Δ_окр – ошибка округления

Δ_окр, (5.1.4.)

где ω – цена деления прибора, или та ее доля, до которой возможен отсчет;

Δ_суб – субъективная ошибка.

6. Вычислить доверительная интервал для α=68% по формуле:

(5.1.5)

7. Результат записать в виде:

вероятность =(число). (5.1.6)

8. Если для величины х известно значение систематической ошибки А (она может быть положительной или отрицательной), то из выборочного среднего нужно вычесть величину этой ошибки, то есть найти разность

, (5.1.7)

на которую следует заменить величину . Напомним, что задавая различное значение вероятности  можно определить соответствующее .

15.2. Косвенные измерения

Пусть требуется измерить величину q=q(x₁, x₂, …, x_n), где x₁, x₂, …, x_n определяют прямыми измерениями.

1. Для каждой величины x_i произвести расчеты по процедуре, описанной в п. 5.1 и записать результаты в виде:

, вероятность =(число). (5.2.1)

2. Вычислить среднее значение функций

. (5.2.2)

3. Вычислить доверительный интервал для величины , соответствующий вероятности=68% по формуле:

(5.2.3)

Если, например, величина (α, β, …, γ – точные числа), то доверительный интервал, как следует из (5.2.3), удобно вычислять по формуле:

(5.2.4)

4. Окончательный результат записать в виде:

, вероятность =(число) (5.2.5).

5. При необходимости доверительный интервал можно рассчитать для большей вероятности, используя формулу (4.4.2).

§6. Метод наименьших квадратов

При выполнении эксперимента часто измеряют две величины х и у, причем у является функцией х. Найденные значения откладывают на графике и пытаются построить кривую, которая наилучшим образом отражает зависимость y = f (x). Ограничимся случаем линейной зависимости

у =  x +  (6.1)

Задача состоит в том, чтобы найти параметры  и α, при которых прямая, выражающая на графике зависимость (16.1), наилучшим образом проходила бы через экспериментальные точки.

Пусть величиных и у измеряются прямым способом, их случайные погрешности распределены по нормальному закону, а систематическими погрешностями можно пренебречь.

Представим все экспериментальные данные х_i и y_i на графике. Геометрически задача измерения  и  состоит в определении параметров некоторой прямой: значения ординаты при нулевом значении абсциссы и тангенса угла наклона соответственно.

По имеющимся точкам на графике можно провести не единственную прямую. Однако, в теория доказывается, что наилучшей прямой будет такая, для которой сумма квадратов разностей

(6.2)

будет минимальна, то есть

. (6.3)

Это условие выполняется, если производные будут равны нулю:

, (6.4)

. (6.5)

Отсюда находим:

, (6.6)

. (6.7)

Из (6.6) и (6.7) следует, что наилучшей оценкой В является следующее выражение:

, (6.8)

а оценкой А:

, (6.9)

где . (6.10)

Используя (6.10) формулу (6.8) можно преобразовать к виду:

(6.11)

Для определения погрешностей бывает достаточно вычислить стандартное отклонение коэффициента В или интервал, в котором с установленной вероятностью может находиться коэффициент . Стандартное отклонение коэффициента В определяется по формуле:

, (6.12)

в которой

, (6.13)

, (6.14)

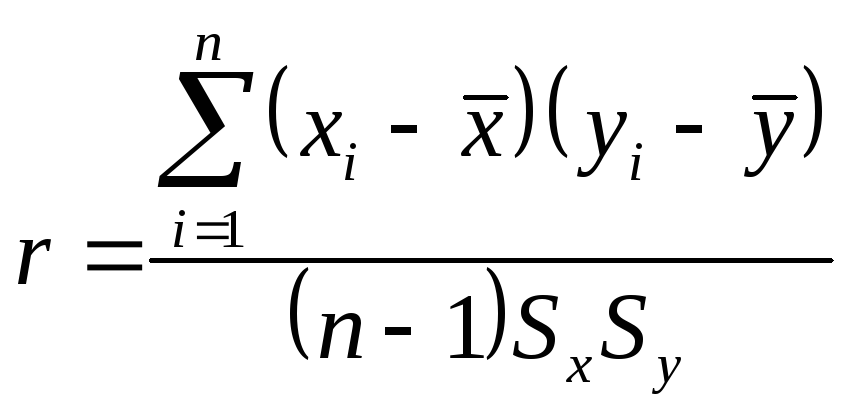, (6.15)

Интервал, в котором с задаваемой вероятностью  может находиться коэффициент В, записывается в виде:

, (6.16)

где В определяется формулой (6.11); S_в – формулой (6.12); t_,n-2 – коэффициент Стьюдента для надежности  и значения параметре n–2; n – число экспериментальных точек (или пар экспериментальных значений x_n, y_n).

Стандартное отклонение коэффициента А определяется по формуле:

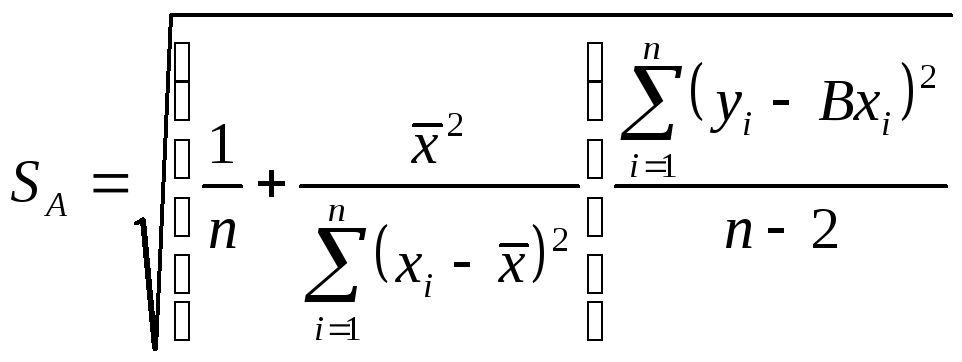, (6.17)

Рассмотрим следующий пример. Пусть произведено десять измерений пар величин х и у. Цифровые значения х могут быть фиксированными, то есть абсолютно точными. Необходимо: определить коэффициенты  и  (см. (6.1)).

Таблица 4

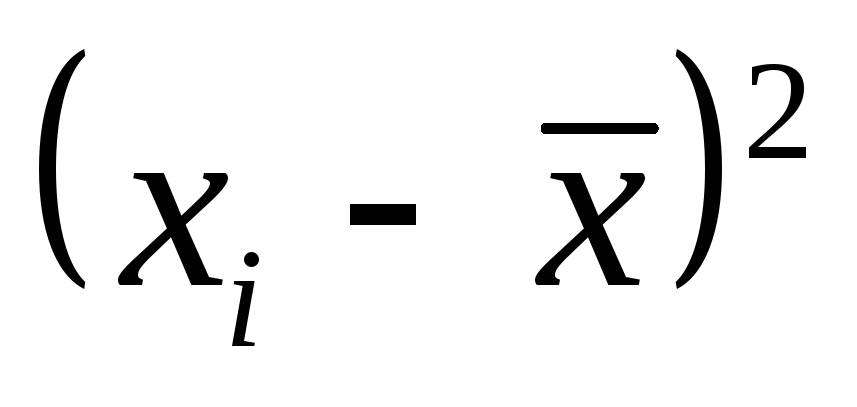
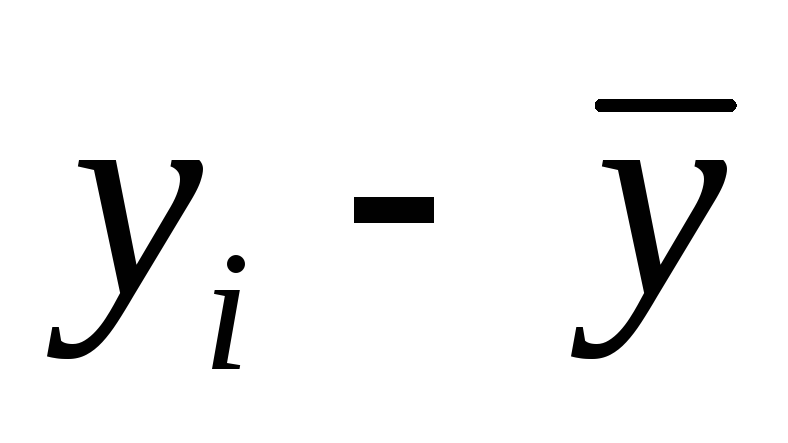
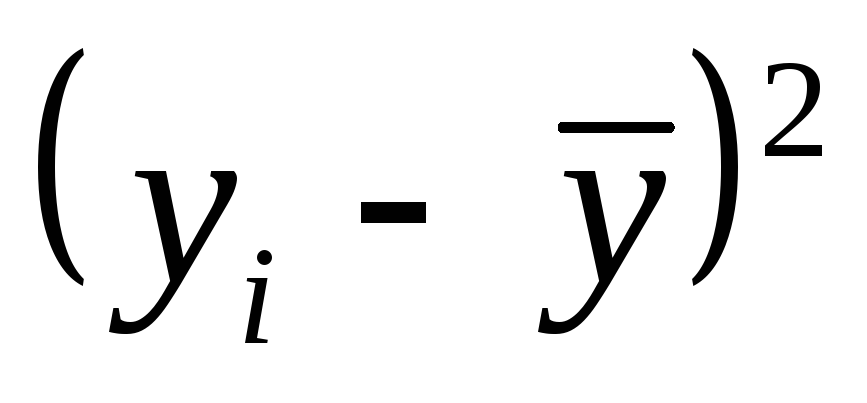
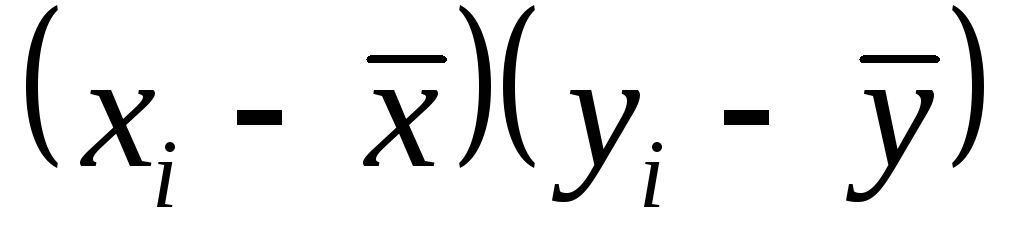
0,2	-0,9	0,81	0,31	-1,36	1,85	1,22
0,4	-0,7	0,49	0,59	-1,08	1,17	0,76
0,6	-0,5	0,25	0,82	-0,85	0,72	0,42
0,8	-0,3	0,09	1,17	-0,50	0,25	0,15
1,0	-0,1	0,01	1,55	-0,12	0,01	0,01
1,2	0,1	0,01	1,87	0,20	0,04	0,02
1,4	0,3	0,09	2,20	0,53	0,28	0,16
1,6	0,5	0,25	2,35	0,68	0,46	0,34
1,8	0,7	0,49	2,65	0,98	0,96	0,69
2,0	0,9	0,81	3,20	1,53	0,44	1,38

По формулам (6.10) находим: =1,1;=1,67.

По формулам (6.9) и (6.11) определяем А и В: А= – 0,02, В=1,54.

Уравнение для наилучшей прямой имеет вид: у = 1,54 х – 0,02.

Оценка стандартного отклонения для коэффициента В рассчитываем по формуле (6.12): S_В=0,11.

Интервал, в котором с вероятностью  = 0,90 находится коэффициент , имеет вид:  = 1,5 ± 0,21, вероятность  = 0,90.

При вычислении интервала использована величина t_{; n-2} = 1,9 (см. Таблицу 1 Приложения).