§4. Средства измерений

Под средствами измерений понимается всё многообразие измерительных инструментов и приборов. Средства измерений разнообразны, но имеют общее назначение и поэтому имеют общую теорию погрешностей. Основной задачей этой теории является расчёт результирующей погрешности средств измерений по отдельным составляющим погрешностей.

4.1. Погрешности средств измерений

Погрешности средства измерений может иметь и систематическую, и случайную составляющие. Систематические составляющие вызываются: неточным нанесением отметок на циферблат; изменением со временем упругих свойств пружины, создающей противодействующий момент; неточной подгонкой сопротивлений резисторов и другими причинами технологического характера. Случайная составляющая погрешности вызывается, например, трением в опорах подвижной части прибора; нестабильностью переходного сопротивления электрических контактов переключателей и другими причинами случайного характера.

Погрешность средств измерений, то есть инструментальная или приборная ошибка, определяется суммой систематической и случайной ошибок.

Ошибки измерительных приборов зависят от условий их работы, температуры, влажности, давления, уровня вибраций и т.д. Условия, при которых делается градуировка приборов, определяются соответствующими стандартами и называются нормальными условиями. Ошибка приборов при нормальных условиях называется основной. Условия, при которых делаются измерения часто не совпадают с нормальными. Возникающая вследствие этого ошибка называется дополнительной.

Градуировку средств измерения осуществляют с помощью образцовых приборов, суммарная погрешность которых, согласно требованиям законодательной метрологии, не должна быть более 1/3 погрешности градуируемых средств измерения. При градуировке получают на графике точки, расположенные в некоторой полосе, по которой проводят плавную среднюю кривую, которую принимают за номинальную градуировочную характеристику средства измерения.

Воздействие различных причин при получении градуировочной характеристики прибора приводит к тому, что многократно снятые характеристики прибора или серии однотипных приборов занимают на графике некоторую полосу, которую называют полосой погрешностей данного типа или данного экземпляра прибора. Полоса погрешностей является обобщённой характеристикой результирующей инструментальной погрешности прибора. Параметры полосы погрешностей определяются положением её границ. На основе полосы погрешностей для каждого типа приборов устанавливаются нормируемые значения погрешности. Под нормируемыми значениями погрешности понимаются границы предельно допустимых значений модуля реальных погрешностей.

Для учёта систематической ошибки прибора используется её рандомизация, сущность которой в следующем. Систематическая ошибка прибора изменяется от одного прибора к другому. Для простоты вся совокупность приборов данного вида характеризуется функцией плотности, стандартным отклонением или интервалом, в который с определённой вероятностью попадает систематическая ошибка , поэтому при работе с прибором в силу отсутствия информации об ошибке конкретного прибора используют распределение ошибок для всей совокупности приборов, то есть учитывают систематическую ошибку как случайную.

Правила, согласно которым назначаются предельные границы погрешностей и форма их записи, то есть вся процедура нормирования погрешностей средств измерения, основывается на системе стандартов, обеспечивающих единство измерений, при этом для разных средств измерения используется абсолютные, относительные или приведённые значения погрешностей.

Абсолютная погрешность выражается в единицах измеряемой величины, например, в милливольтах, амперах, кельвинах и т.д. её использование удобно для однозначных мер, но мало удобно для широкодиапазонных приборов. Пределы допускаемой абсолютной погрешности устанавливаются по формулам:

(4.1.1)

, (4.1.2)

где ∆ – пределы допускаемой абсолютной погрешности, выраженные в единицах измеряемой величины; x – значение измеряемой величины; a, b – положительные числа, не зависящие от x.

Приведённая погрешность определяется как отношение абсолютной погрешности прибора, выраженной в единицах измеряемой величины, и протяжённости диапазона измерения прибора и выражается в десятичных дробях или в процентах. Пределы допускаемой приведённой основной погрешности устанавливаются по формуле:

, (4.1.3)

где δ – пределы допускаемой основной приведённой погрешности в процентах; ∆ – устанавливается по формуле (4.1.1), что означает – ширина полосы погрешностей остаётся постоянной на всём диапазоне измерений, то есть остаются постоянными пределы допускаемой абсолютной основной погрешности; x_k – нормирующее значение, выраженной в тех же единицах, что и ∆ (как правило, ∆ – предел измерения на данном диапазоне, но если нуль шкалы находится посередине, под ∆ – понимают модуль разности положительного и отрицательного пределов); q – отвлечённое положительное число, выбираемое из следующего ряда:

1·10ⁿ, 1,5·10ⁿ, 2·10ⁿ, 2,5·10ⁿ, 4·10ⁿ, 5·10ⁿ, 6·10ⁿ, (4.1.4)

где n = 1, 0, – 1, – 2 и так далее.

Число q определяет класс точности прибора. Так, согласно ГОСТ 1845-59, электроизмерительные приборы делятся на восемь классов точности: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4. Класс точности определяет наибольшую приведённую ошибку для всего рабочего диапазона в процентах. Из формулы (4.1.3) следует, что наибольшая абсолютная погрешность для всего диапазона:

(4.1.5)

Например, для милливольтметра со шкалой до 50 мВ, имеющего класс точности 0,5 абсолютная погрешность не превышает ∆=±0,5·50 мВ/100=±0,5 мВ. Полная погрешность измерения должна включать также погрешность отсчёта по шкале.

Пределы допускаемой относительной основной погрешности средств измерения устанавливаются по формуле:

, (4.1.6)

где q – отвлечённое положительное число, выбираемое из ряда (4.1.4); x – показания прибора. Так как класс точности прибора q – величина постоянная, абсолютная приборная погрешность

(4.1.7)

оказывается пропорциональной x, то есть возрастает от нуля, в начале диапазона измерений, до максимального значения в конце. Примером таких приборов могут служить магазин ёмкостей (ГОСТ 6746-75, класс точности 0,5) или магазин сопротивлений (ГОСТ 7003-64, класс точности 0,2). На самом деле абсолютная приборная погрешность практически никогда не может обращаться в нуль в начале диапазона измерений. Для учёта этого факта относительная погрешность прибора может устанавливаться по формуле:

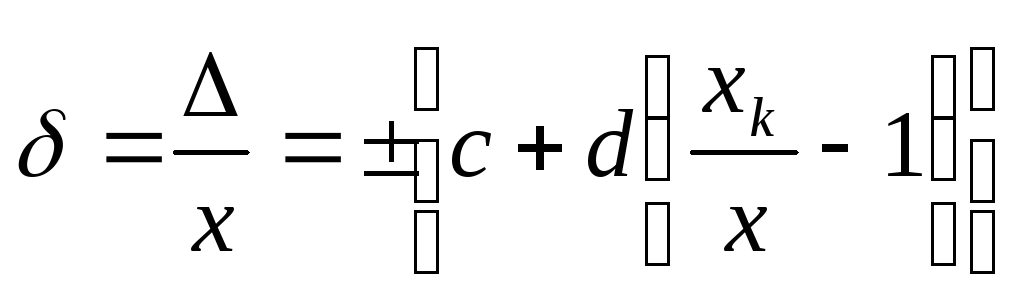, (4.1.8)

где x_k – больший по модулю из пределов измерений; c и d – положительные числа, выбираемые из ряда (4.1.4). Класс точности прибора в этом случае обозначается двумя числами, разделёнными косой чертой c/d. Примером такого прибора может служить магазин сопротивлений (ГОСТ 23734-79) класса точности 0,2/6·10^-6.

4.2. Погрешности некоторых измерительных приборов

ИЗМЕРИТЕЛЬНЫЕ ЛИНЕЙКИ

а) Стальные измерительные линейки (ГОСТ 427-56)

Деления нанесены через 1 мм. Допускаемая предельная погрешность при длине линейки 300 мм, 500 мм и 1000 мм составляет, соответственно, ±0,10 мм; ±0,15 мм; ±0,20 мм. Ошибку округления в определении долей деления шкалы на глаз следует учесть в соответствии с п. 4.3. Но и при соблюдении описанных в этом параграфе правил, ошибку отсчёта долей деления на глаз следует принимать не менее чем 0,2 деления.

б) Деревянные и пластмассовые линейки (ГОСТом не нормируются).

За основную предельную ошибку для деревянных линеек следует принимать ±0,5 мм, а для пластмассовых ±1,0 мм.

ШТАНГЕНЦИРКУЛИ (ГОСТ 166-73)

Выпускаются различные штангенциркули, пределы измерения которых изменяются от 125 мм до 2500 мм. Основной частью штангенциркуля является нониус – отчетная устройство с дополнительной шкалой, цена деления которой меньше, чем цена деления основной шкалы. Точность штангенциркуля с нониусов равна разности цены деления основной шкалы и цены деления шкалы нониуса. Для штангенциркулей с точностью 0,1 мм предельная основная приборная погрешность прибора равна ±0,1 мм, а для штангенциркулей с точностью 0,05 мм составляет ±0,05 мм. Кроме этого следует учитывать ошибку округления. Её максимальное значение равно половине точности.

МИКРОМЕТРЫ (ГОСТ 6507)

Микрометры позволяют производить изменения точнее, чем штангенциркули. Цена деления круговой шкалы микрометра равна 0,01 мм. Основная предельная приборная ошибка для микрометра при измерении размеров до 3 мм не превышает ±0,002 мм, а при измерении больших размеров не превышает ±0,004 мм. При работе в физической лаборатории следует также учитывать погрешность округления при измерении и погрешность при установке нулевого деления. Максимальная погрешность округления, очевидно, равна ±0,005 мм.

ИЗМЕРЕНИЕ ВРЕМЕНИ

В лабораториях при измерении времени часто используются механические секундомеры с ценой деления 0,1 с или 0,2 с. Основная предельная ошибка этих секундомеров равна цене деления. Вместе с этим механические секундомеры обладают ошибкой хода, которая, например, для секундомеров типа С-1, С-2, СМ-60 могут достигают ±1,5 с за 30 минут хода (ГОСТ 5073-62). Следует также учитывать, что при включении и остановке механических секундомеров возникает субъективная ошибка, связанная с несовершенством органов чувств (в данном случае с неидеальной реакцией) любого экспериментатора. Эта погрешность, как показали специальные исследования, может достигать ±0,3 с. В учебных лабораториях также используются электронные счётчики-секундомеры ССЭШ, точность которых составляет 0,01 с. Основная предельная погрешность для этих приборов (ГОСТ 6836-72) составляет ±(0,02·t+0,01) с.

НАБОР ГИРЬ

По допускаемой погрешности гири делятся на пять классов точности. Набор гирь, используемых в учебной лаборатории, соответствует четвертому классу точности. В. представленной таблице указываются основные предельные погрешности этих гирь.

Таблица 2

Номинальное значение, г	100	50	20	10	5	2	1
Основная предельная погрешность, мг	±40	±30	±20	±12	±8	±6	±4
Номинальное значение, мг	500	200	100	50	20	10	5
Основная предельная погрешность, мг	±3	±2	±1	±1	±1	±1	±1

Набор гирь для настольных (торговых) весов ВТ-200 относится к пятому классу. Допускаемые отклонения гирь, используемых с этими весами, указаны в следующей таблице.

Таблица 3

Номинальное значение, г	1000	500	200	100	50	20	10	5
Основная предельная погрешность, мг	±600	±400	±300	±200	±150	±100	±60	±40

4.3. Ошибки округления

При считывании показаний со шкалы прибора всегда возникает ошибка, связанная с округлением числа, которую рассматривают как случайную величину. Функция распределения этой случайной величины может быть определена следующей формулой.

(4.3.1)

З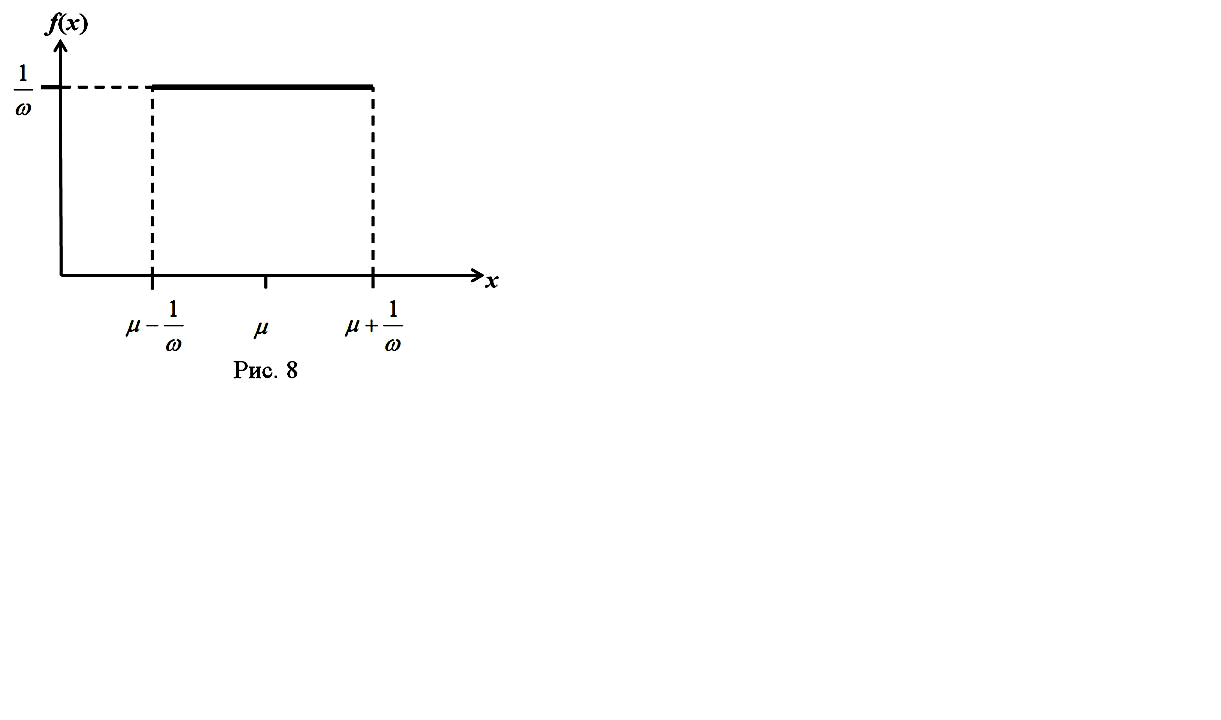десьω – цена деления прибора или та ее доля до которой возможен отсчет; μ – значение физической величины, соответствующее определенной отметке шкалы. Такое распределение называют прямоугольным или равномерным. График этой функции представлен на Рис. 8.

Зная функцию распределения f(х) можно определить среднее значение (см. формулу (3.1.5)):

(4.3.2)

Вероятность того, что случайная величина лежит в интервале (0 ≤α ≤ 1) равна площади прямоугольника со сторонами иαω:

(4.3.3)

Таким образом, задавая определенную вероятность α, мы можем определить интервал, в который случайная величина х будет заключена с этой вероятностью.

4.4. Неравенство Чебышева

В ряде случаев функция распределения может быть неизвестной, однако при этом возникает вопрос о вероятности попадания случайной величины в заданный интервал. Оказывается, ответ на этот вопрос, можно получить, если известно среднее значение и дисперсия случайной величины. Для этого случая П.Л.Чебышев получил неравенство для оценки вероятности того, что случайная величина х не отличается от своего среднего значения на величину, большуюγσ_x (γ – положительное число):

. (4.4.1)

Для определения вероятности P=α отсюда можно найти число γ>0, при котором неравенство (4.4.1) будет выполняться:

. (4.4.2)

Другими словами, неравенство Чебышева утверждает, что вероятность попадания случайной величины х в интервал , не меньшеα (γ – определяется из (4.4.2)).