§3. Статистический анализ случайных погрешностей

При выполнении многократных измерений необходим метод, который позволил бы обрабатывать полученные результаты. Одним из удобных методов является использование распределения. Предельным распределением (при бесконечном количестве измерений) результатов эксперимента является распределение Гаусса (отметим, что оно не является единственно возможным).

Вопросу обоснования применимости распределения Гаусса в теории ошибок в литературе уделяется много внимания. Но лучше всего, касаясь этого вопроса, пожалуй, сказал тот, кто сказал «экспериментаторы верят в него, полагаясь на доказательства математиков, а математики – полагаясь на экспериментальное обоснование». Тем не менее, распределение Гаусса можно в какой-то мере обосновать.

3.1. Предельное распределение

Результаты серии измерений одной величины можно наглядно представить, построив диаграмму, которая показала бы, как часто получены те или иные значения. Такая диаграмма называется гистограммой.

Вначале рассмотрим измерение величины, которая может принимать дискретные значения. Пусть, например, выполняется подсчет частиц, которые регистрируются счетчиком за одну минуту. Будем считать, что выполнено десять измерений и получены следующие результаты: 56, 59, 54, 58, 56, 57, 56, 58, 57, 57. Эти результаты удобно записать в виде следующей таблицы, располагая их по мере возрастания значения.

Таблица 1

Значения хk	54	55	56	57	58	59
Число реализаций nk	1	0	3	3	2	1

Полученные результаты позволяют вычислить среднее значение регистрируемых за одну минуту частиц:

, (3.1.1)

где N – число измерений. Величину, определяющую долю от полного числа измерений, в которой реализуется результат x_к принято называть частотой:

. (3.1.2)

При этом среднее значение можно определить по формуле:

. (3.1.3)

ЧастотыF_k характеризуют распределение результатов измерения в виде гистограмм, на которых по вертикальной оси откладывают значения F_k, а по горизонтальной – x_k.

Если сложить частоты всех возможных значений x_k , то в результате получается единица

. (3.1.4)

Это условие называют условием нормировки.

Г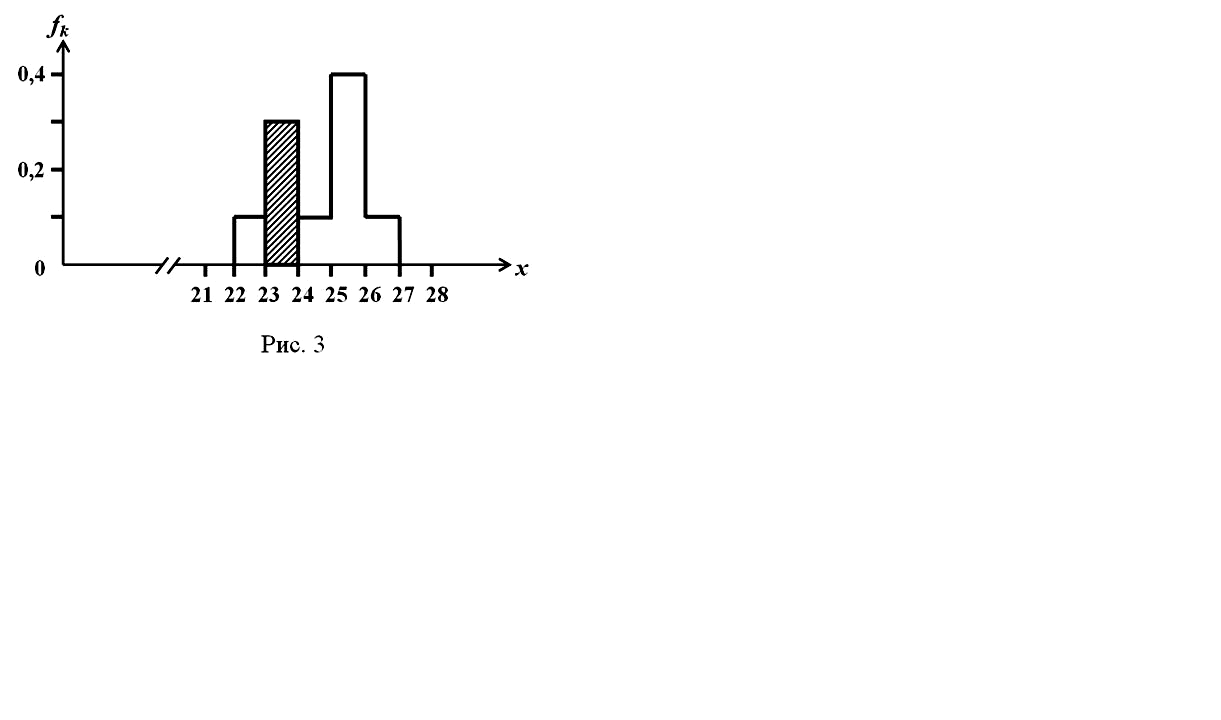истограмма, представленная на Рис. 2, определяет распределение дискретной величины. Вместе с этим, зачастую встречаются физические величины, имеющие непрерывный диапазон возможных значений. Например, при измерении расстояния между двумя точками с помощью линейки с ценой деления 1мм, могут быть получены следующие результаты (в сантиметрах): 26,4; 23,9; 25,1; 24,6; 22,7; 23,8; 25,2; 23,7; 25,3; 25,4. Если по полученным результатам построить гистограмму, подобную предыдущей, то она будет содержать десять черточек одинаковой высоты и являться малоинформативной. Поэтому диапазон возможных значений разбивают на интервалы и подсчитывают, какое количество измерений попадает в каждый интервал. Выбирая интервал в размере Δ_k=1,0 см, можно построить представленную на Рис. 3 гистограмму для непрерывной функции. Причем для непрерывной величины площадь f_k·Δ_k к-го прямоугольника (на Рис. 3 он заштрихован) имеет такой же смысл, что и высота к-той черточки F_k в случае гистограммы для дискретной величины (см. Рис. 2).

При увеличении числа измерений N можно уменьшить ширину интервала Δ_k. Так на Рис. 4а представлена гистограмма в случае ста измерений того же расстояния x при Δ_k=1,0 см, а на Рис. 4б – в случае тысячи измерений при Δ_k=0,5 см.

Гистограммы на Рис. 4 иллюстрируют важное свойство большинства измерений: с ростом числа измерений их распределение стремится к некоторой определенной непрерывной кривой – предельному распределению, которая соответствует гистограмме при N и Δ_k0.

При наличии только случайных погрешностей предельное распределение представляет собой симметричную колоколообразную кривую, показанную на Рис.4б. Конечно, предельное распределение – теоретическая идеализация, которую никогда нельзя точно получить в эксперименте.

Предельное распределение определяет функцию, называемую плотностью распределения, которую обозначим f(x). Если известна функция f(x), можно разделить весь интервал значений x на малые интервалы от x_k до x_k+Δx_k. Тогда доля значений, попавшая в каждый такой интервал, будет F_k=f(x_k)·Δx_k и формула (3.1.3), определяющая среднее значение величины, в пределе, когда все интервалы стремятся к нулю примет вид

(3.1.5)

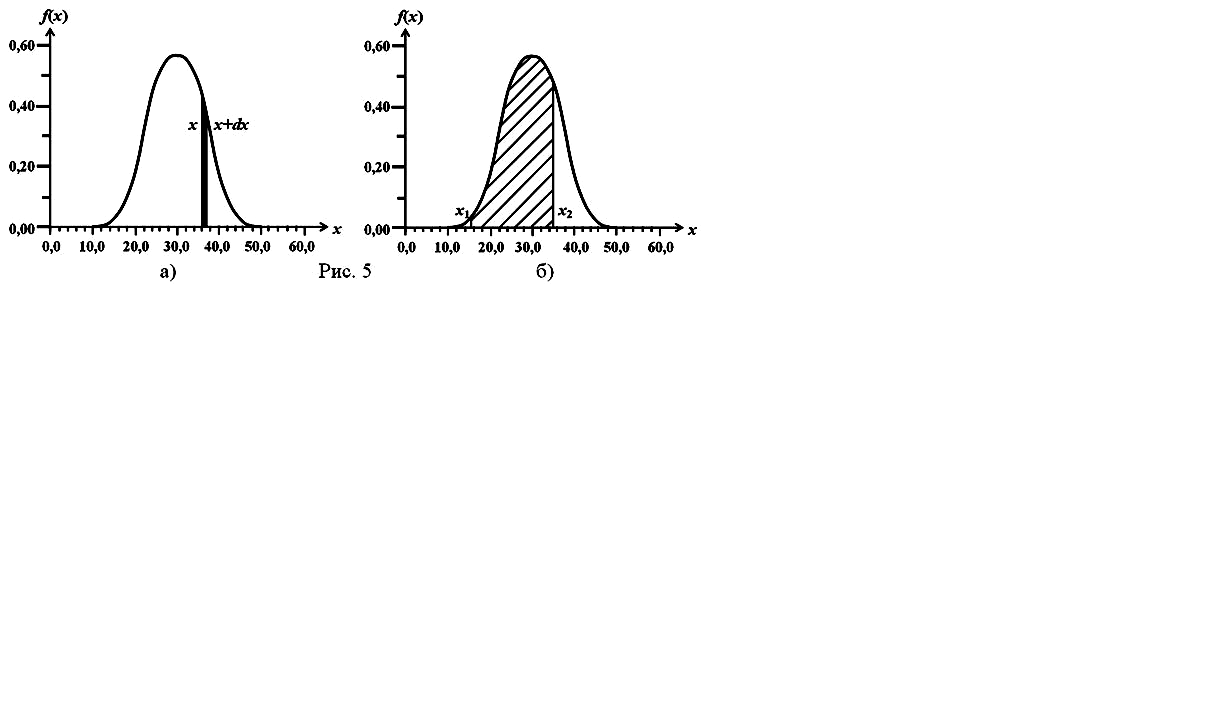
Доля измерений (при N), которая попадает в любой бесконечно малый интервал от x до x+dx , будет равна площади f(x)·dx заштрихованного участка на Рис.5а. В случае интервала конечной ширины. например от x₁ до x₂ , доля от полного числа измерений, попадающих в данный интервал равна площади под кривой между x=x₁ и x=x₂ (Рис.5б). Она определяется путем интегрирования: доля измерений в интервале от x₁ до x₂ равна .

Сказанное можно выразить другим очень полезным способом:

– (3.1.6)

– данный интеграл определяет вероятность попадания любого единичного измерения в интервал от x = x₁ до x = x₂.

Отсюда можно сделать важное заключение: если бы было известно предельное распределение f(x) для результатов измерений данной величины x, то можно найти вероятность получения результата в любом заданном интервале x₁  x  x₂.

Предельное распределение f(x) должно удовлетворять условию нормировки (аналогично (3.1.4) для дискретной функции):

, (3.1.7)

которое означает, что при единичном измерении вероятность получения результата в пределах от – до + равна единице.

Наиболее употребительной мерой, характеризующей рассеяние случайной величины, является дисперсия, обозначаемая D_x и определяемая по формуле:

. (3.1.8)

По аналогии с (3.1.5), когда N дисперсия определяется через функцию распределения

. (3.1.9)

Квадратный корень из дисперсии называется среднеквадратичным или стандартным отклонением и обозначается _x

. (3.1.10)

3.2. Функция Гаусса

В математике функция, график которой имеет форму колоколообразной кривой, называется функцией нормального распределения или функцией Гаусса. Она имеет следующий вид:

. (3.2.1)

Функция Гаусса описывает предельное распределение результатов измерений величины x, истинное значение которой равно X. Причем при измерении величины x сказываются только случайные ошибки. Принято считать, что результаты измерений распределены нормально, если их предельное распределение описывается функцией Гаусса.

В формуле (3.2.1) величина σ является фиксированным параметром, который определяет ширину гауссовой кривой в точках перегиба. Малые значения σ приводят к распределению типа острого пика, которое соответствует более точным измерениям, в то время как большие значения σ дают широкое распределение, соответствующее измерениям с малой точностью. На Рис.6 представлены два примера графиков функций Гаусса с различными значениями величин

Х и σ. Видно, что величина σ в знаменателе предэкспоненциального множителя формулы (3.2.1) обеспечивает для более узкого распределения (малые σ) большую высоту в точке x=X. Это обусловлено тем, что функция Гаусса нормирована, то есть для нее выполнено условие (3.1.6). Поэтому площадь под кривой, выражающей на графике функцию Гаусса, при любых значениях σ и X должна равняться единице.

Функция Гаусса отражает следующие предположения, лежащие в основе теории случайных погрешностей и подтверждаемые опытом:

1. Погрешности результатов наблюдений принимают непрерывный ряд значений.

2. При большом числе наблюдений одинаково часто встречаются погрешности одного значения, но разных знаков.

3. Частота появления погрешностей уменьшается с возрастанием их значений.

В случае распределения Гаусса среднее значение величины X определяется, согласно (3.1.5), по формуле:

. (3.2.2)

Интеграл вычисляется аналитически, что приводит к следующему результату:

(3.2.3)

Отсюда можно сделать вывод: если результаты измерений распределены в соответствии с функцией Гаусса, то в случае бесконечно большого числа измерений среднее значение будет равно истинному значениюX, которое соответствует центру функции Гаусса.

Для дисперсии (3.1.9) в случае распределения Гаусса получим

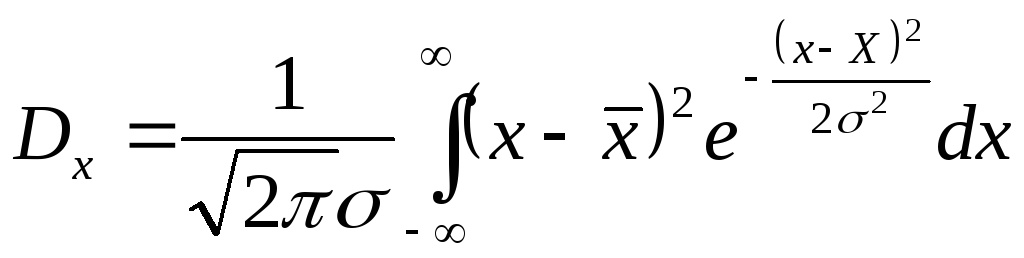(3.2.4)

Результат аналитического интегрирования:

(3.2.5)

Поскольку, согласно (3.1.10), корень из дисперсии есть стандартное отклонение, то

. (3.2.6)

Следовательно: параметр σ ширины функции Гаусса есть стандартное отклонение, которое мы получили бы в случае бесконечно большего числа измерений.

3.3. Вероятность попадания результата однократного измерения в заданный интервал

Для распределения Гаусса вероятность попадания результата измерения в определённый интервал при однократном измерении, согласно (3.1.6), определяется по формуле:

P(в пределах tσ), (3.3.1)

где t – положительное число, tσ – полуширина задаваемого интервала.

После подстановки ,dx=σdz получим:

Р(в пределах tσ)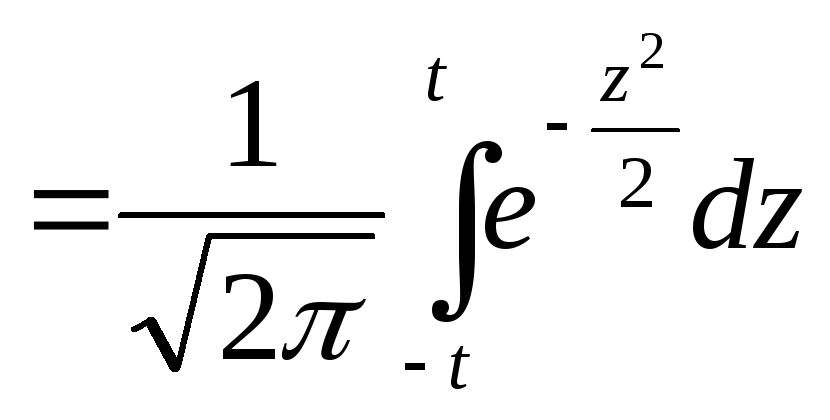(3.3.2)

Этот интеграл называют функцией ошибок (или нормальным интегралом ошибок), который обозначаетсяerf(t). Его значение при произвольном t аналитически не вычисляется и определяется только численными методами. В таблице 1 Приложения приведены значения функции ошибок для различных значений t. Вероятность может быть определена как в виде десятичной дроби, так и в процентах. На Рис. 7 изображена зависимость функции ошибок от параметра t в процентах.

Из Таблицы 2 Приложения или Рис.7 видно, например, что вероятность попадания в интервал полуширина которого соответствует одному стандартному отклонению σ равна 68%, 2σ – 95%, 3σ – 99,7%, то есть с увеличением t вероятность попадания в интервал с пределами tσ быстро стремиться к 100%.

Используя Таблицу 2 Приложения легко определить вероятность попадания результата единичного измерения в интервал с произвольными границами x₁ и x₂, то есть когда x₁ и x₂ отличаются от X на одинаковое значение tσ.

Вероятность того, что ожидаемый результат однократного измерения окажется вне определённого интервала можно определить по формуле:

Р(вне tσ) = 100% – Р(в пределах tσ). (3.3.3)

Поэтому, например, вероятность попадания результата единичного измерения за пределы интервала с полушириной tσ от истинного значения Х очень мала и составляет всего 0,3%.

3.4. Прямые измерения

В реальных условиях число измерений конечно. Если, например, сделано N измерений величины x (то есть некоторый эксперимент независимо повторен N раз), то полученные результаты x₁, x₂, …, x_N называют случайной выборкой объёма N из множества всех возможных значений величины x.

В теории обработки результатов эксперимента строго доказывается, что в этом случае наилучшей оценкой истинного значения X является выборочное среднее значение из N измерений:

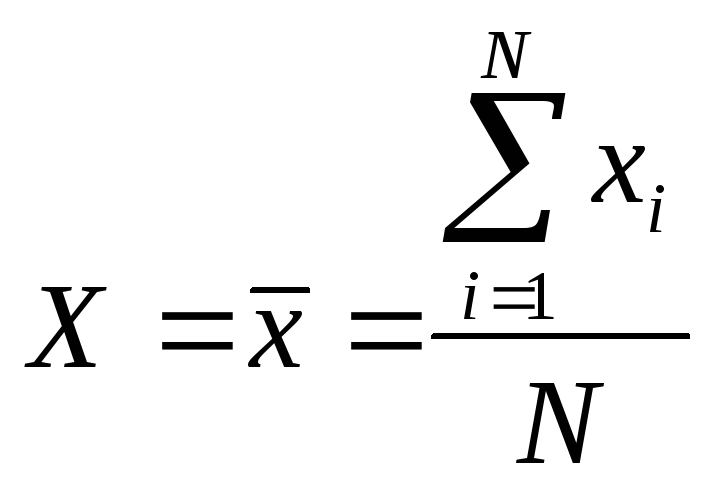(3.4.1)

Кроме того, наилучшей оценкой стандартного отклонения σ_x является выборочное среднее квадратичное отклонение S_x:

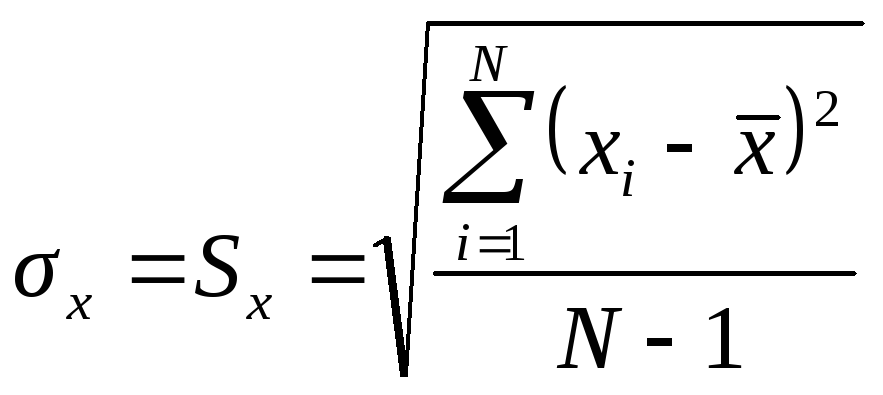(3.4.2)

3.5. Отбрасывание результатов прямых измерений

Ранее было сказано, что среди погрешностей измерений могут встречаться промахи – погрешности, существенно превышающие ожидаемые значения при данных условиях эксперимента. Поэтому возникает естественный вопрос – какие погрешности следует считать промахами с целью исключения в дальнейшем соответствующих им результатов измерения? Эта оценка осуществляется на основе критерия Шовене.

Пусть проделано N измерений некой величины x и получены следующие результаты: x₁, x₂, …, x_N. На основании этих значений по формулам (3.4.1) и (3.4.2) можно вычислить иS_x. Если имеется подозрительный результат, погрешность которого, возможно, является промахом, то для него вычисляют

– (3.5.1)

число выборочных стандартных отклонений, на которое x_под отличается от . По таблице 2 Приложения можно найти вероятностьР(вне τ_подS_x) того, что нормальное измерение будет отличаться от наτ_под или более выборочных стандартных отклонений. Наконец, следует умножить полученную вероятность Р(вне τ_подS_x) на полное число измерений N, чтобы получить

n(хуже, чем x_под) = N·P(вне τ_подS_x), (3.5.2)

которое определяет число ожидаемых измерений, которые дают столь же плохие результаты, что и x_под. Если n<0,5, то x_под отбрасывается. В этом состоит критерий Шовене. После отбрасывания результата, не удовлетворяющего критерию Шовене, надо пересчитать иS_x по оставшимся данным. При n>0,5 следует всё оставить без измерения.

Рассмотрим пример: пусть произведено шесть измерений некоторой величины и получены следующие результаты: 3,8; 3,5; 3,9; 3,9; 3,4; 1,8. Среди этих результатов подозрительным является 1,8. Поэтому с учётом шести измерений рассчитываем =3,4 иS_x=0,8. Значение 1,8 отличается от на 2S_x. Согласно Таблицы 2 Приложения:

Р(вне 2S_x) = 1 – Р(в пределах 2S_x) = 0,05.

То есть из двадцати возможных результатов измерений приблизительно только один должен также сильно отличаться от как число 1,8. В случае проведённых шести измерений ожидаемое число таких результатовn=0,05·6=0,3. Поскольку n<0,5, то, согласно критерию Шовене, подозрительный результат x=1,8 должен быть исключён, а для оставшихся значений =3,7;S_x=0,23.

3.6. Косвенные измерения

Теперь следует привести результаты, которые получены в теории измерений для случая, когда производятся косвенные измерения величины q(x, y, …., z). Причём величины x, y, …, z могут быть зависимыми.

Пусть производится конечное число измерений, но на результат измерений оказывает влияние только случайные погрешности. Если погрешности при измерении x, y,…, z малы, то существует строгое доказательство, что наилучшей оценкой значения q является

, (3.6.1)

где определяются по формуле (3.4.1).

Оценка стандартного отклонения при косвенных измерениях определяются выражением:

, (3.6.2)

где S_x, S_y, …, S_z являются выборочными стандартными отклонениями, определяемыми по формуле (3.4.2). После вычисления частных производных в полученных выражениях осуществляется подстановка .

3.7. Стандартное отклонение среднего

Предположим, что результаты измерений величины x распределены нормально около истинного значения X с шириной σ_x. Необходимо узнать, какова надёжность среднего значения для N измерений. Для ответа на этот вопрос представим себе, что N измерений повторяются много раз, причём в каждом случае определяется среднее значение . Нас интересует, как распределены полученные значения.

Величина есть простая функция измеренных значенийx₁, x₂, …, x_N

. (3.7.1)

Поэтому можно найти распределение с помощью расчёта ошибок для косвенных измерений.

Поскольку каждое из измеренных значений x₁, x₂, …, x_N распределено нормально, то очевидно, что и также имеют нормальное распределение. Так как истинным значением дляx₁, x₂, …, x_N является X, то и истинным значением является такжеX. Следовательно, полученные значения распределены нормально около истинного значенияX. Ширину этого распределения можно найти по формуле:

. (3.7.2)

Но:

, (3.7.3)

а из (3.7.1) следует:

. (3.7.4)

Следовательно, вместо (3.7.2) получаем:

. (3.7.5)

Эту величину называют стандартным отклонением среднего. Видно, что при N значение .

Вывод: значения распределены нормально с центром, равным истинному значению и с шириной; другими словами, если найдено однажды , то вероятность попадания этого значения в интервалравна 68%.

Для оценки стандартного отклонения среднего, которое обозначим , используют формулу

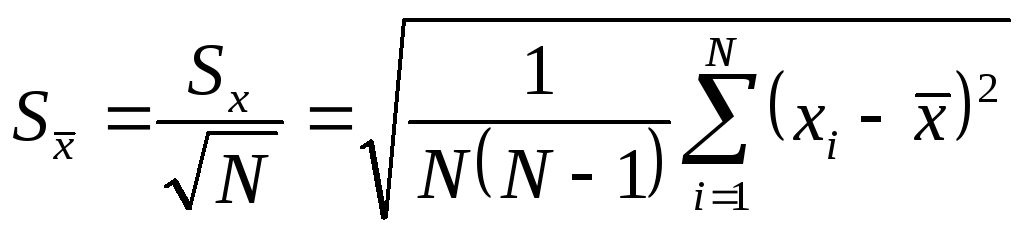(3.7.6)

Величину называют выборочным стандартным отклонением среднего. Видно, что при увеличении числа измеренийN растёт точность измерения. Стандартное отклонение среднего при косвенных измерениях может быть определено по формуле:

(3.7.7)

Рассмотрим следующий пример: определим выражение для стандартного отклонения величины q, которая связана с величинами x, y, z, определяемыми прямыми измерениями, следующим соотношением:

, (3.7.8)

где α, β, γ – точные числа.

Для частных производных получаем:

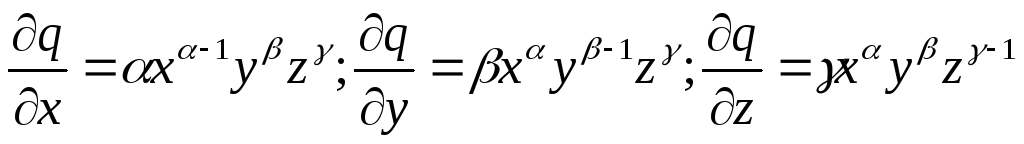. (3.7.9)

После подстановки (3.7.9) в (3.7.7) имеем:

. (3.7.10)

3.8. Распределение Стьюдента

Ранее было показано, что величина является лишь наилучшей оценкой истинного значения измеряемой величины. Вместе с этим, наилучшей оценкой стандартного отклонения среднего является величина. Таким образом, мы имеем дело с некоторыми приближениями. Ясно, что распределение случайных погрешностей будет тем существенней отличаться от функции Гаусса, чем меньше выполнено измерений.

Английский химик и математик В.С. Госсет, публиковавший свои работы под псевдонимом Стьюдент, получил формулу для нахождения распределения погрешностей средних значений, получаемых при конечном числе измерений. Причём им была получена зависимость вероятности попадания получаемого результата в определённый интервал от числа измерений. Однако эта зависимость имеет сложный характер и не выражается через элементарные функции.

На основе распределения Стьюдента были составлены таблицы коэффициентов Стьюдента t_α,n, которые показывают во сколько раз нужно увеличить величину , чтобы при определённом числе измеренийn получить задаваемую вероятность (надёжность) n. Коэффициенты Стьюдента представлены в Таблице 1 Приложения.

В результате можно записать:

, (3.8.1)

где – доверительный интервал, который означает, что истинное значение измеряемой величины находится в интервалес вероятностью или надёжностьюα, где

. (3.8.2)