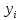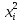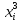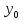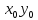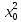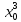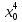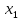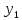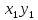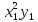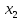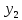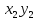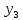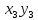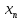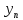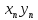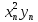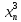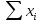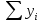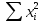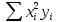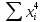112

Погрешность интерполяции

R(x)=f(x)-P_N(x), где R(x)–погрешность.

Т.к. полином можно рассматривать как основную часть разложения ф-и в степенной ряд, то R(x) должен быть полиномом более высокой степени, чем P_N(x). Тогда R(x)=k*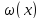. k–константа, значение которой зависит от вида интерполируемой ф-и и значения х в области интерполяции. Пусть ф-я f(x) непрерывна, n+1 раз дифф-ма на отрезке интерполяции [x₀,x_N]. Тогда K=.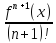

R(x)=.

Оценка предельно допустимой погрешности выч-ся по формуле:

Q(x).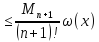

M(x+1)–максимальное значение модуля (n+1) производной ф-и на отрезке [x₀,x_N].

Достоинства и недостатки интерполяционных многочленов Ньютона и Лагранжа

Если к интерполяционной таблице добавить еще один узел, то в инт-м многочлене Ньютона добавится еще одно слагаемое, однако значение остальных разностей не изменится.

В тоже время все сомножители в инт-м мн-не Лагранжа придется пересчитать.

Однако инт-й мн-н Лагранжа позволяет на одной и той же инт-й сетке интерполировать несколько функций.

В инт-х мин-х Ньютона все разделенные разности придется пересчитывать.

Квадратичная интерполяция

S=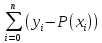² стремится к минимуму

S=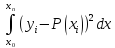 стремится к минимуму.

Квадратичная инт-я используется когда значения найдены с погрешностями.

Прежде чем определить вид функциональной зависимости P(x) необх. нанести экспериментальные точки на график с тем, чтобы можно было определить вблизи какой функциональной кривой группируются эти точки.

S= стремится к минимуму.

Необходимо вычислить коэфф-ты a,b,c, которые бы обеспечили минимум величины S.

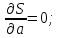
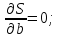
Вместо 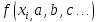подставляем ()

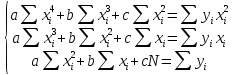
Получена система лин уравнений относ-но a,b,c:

			..
			…
			…

Численное дифференцирование

Задачи числ-го д-я можно разделить на 2 класса:

1. ф-я задана аналитически

2. ф-я задана таблично.

Будем полагать, что ф-я явл-ся непрерывной и плавной. Пусть она задана аналитически: y’=.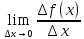

При вычислении производной численно предел отношения заменяется конечно разностным отношением : y’= .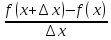

Чем меньше , тем ближе найденное значение к точному значению производной.

Если задано требуемое значение точности нахождения производной, то подбор 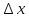можно осуществить по след алгоритму:

Пусть заданы начальные значения точка х, в которой находится значение производной.

Тогда найдем значения :

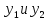и

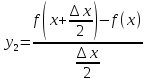
если 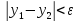=> stop

иначе

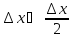
Для нах-я производных высших порядков можно разложить исходную функцию в ряд Тейлора:

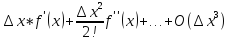
=f(x)+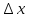

f(x-)= f(x)-

Сложим эти выражения:

f’’(x)=

погрешность имеет порядок ()

f’(x)==()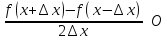

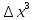Используя данный подход с учетом разложений можно выразить значения производных любого порядка. Подобный же подход исп-ся для нах-я частных производных любого порядка. Для этого ф-ю нескольких переменных разлагают в ряд Тейлора по всем аргументам функции.