11. Элементы численного анализа

В задачах этого раздела требуется реализовать заданные численные методы, экспериментально исследовать условия и скорость сходимости методов. В условиях задач, как правило, дается лишь основная идея каждого метода. Рекомендуется самостоятельно познакомиться с обоснованием и условиями применения метода по специальной литературе, например:

1. Демидович Б. П., Марон И. А. Основы вычислительной математики. — М.: Наука, 1970.

2. Калиткин Н. Н. Численные методы. — М.: Наука, 1978.

3. Бахвалов Н. С. Численные методы. — М.: Наука, 1973.

4. Бронштейн И. М., Семендяев К. А. Справочник по математике. — М.: Наука, 1978.

Вычисление функций и их производных, используемых в задачах, рекомендуется оформлять в виде подпрограмм, так чтобы можно было подставлять любую функцию, не меняя самой программы. Погрешность, начальные условия и параметры алгоритма задаются вводом. Там, где это возможно, рекомендуется тестировать алгоритм на примерах, для которых известно или может быть найдено аналитически точное аналитическое решение (например, результат численного интегрирования сравнить с известной первообразной). Кроме собственно программирования и тестирования алгоритма полезно провести исследование предложенного метода на сходимость и скорость сходимости при разных условиях, устойчивость для разных функций и разных начальных условий.

Пример. Рассмотрим решение задачи 11.6 — вычисление определенного интеграла по формуле прямоугольников. В качестве подынтегральной функции возьмем у = е, для которой первообразная не выражается в элементарных функциях (это одна из разновидностей интеграла вероятности), поэтому завершение итерационного процесса — увеличение числа отрезков разбиения — запишем по условию близости соседних приближений, а не близости точного и приближенного результатов. Кроме того, встроенная функция Ехр(х) не может быть вычислена при больших (по модулю) значениях аргумента, поэтому вводим ограничение на задаваемые пределы интегрирования — не более чем [-5; 5], так как подынтегральная функция за пределами этого отрезка практически равна нулю. Решение может быть представлено с помощью следующей программы:

Тестирование. Для испытаний возьмем данные с известным результатом. Так, известно, что

Задачи по теме «Элементы численного анализа»

11.1 (5 6.) Метод простой итерации. Решить методом итераций уравнение вида х = ф(х). Очередное приближение корня находится по формуле ; начальное приближениеx₀ задается произвольно. Обратите внимание, что метод сходится, если только .

11.2 (5 б.) Метод Ньютона. Решить методом Ньютона уравнение f(x) = 0. Очередное приближение корня находится по формуле:

11.3 (6 б.) Метод Эйткена-Стеффенсона (развитие метода простой итерации). Найти решение уравнения методом Эйткена-Стеффенсона, в котором от заданного начального х₀ три очередных приближения находятся по формулам:

Процесс продолжается до достижения одного из условий: .

11.4 (5 б.) Метод дихотомии. Решить уравнение f(x) = 0 методом деления отрезка пополам (методом дихотомии). На каждой итерации отрезок [а, b] делится пополам и выбирается та из половин, на концах которой функция f(x) имеет значения разных знаков.

11.5 (5 б.) Метод хорд. Найти решение уравнения f(x) = 0 на заданном отрезке ахb методом хорд, в котором очередное приближение находится по формуле:

В задачах на численное интегрирование (задачи 11.6-11.8) определенный интеграл требуется найти с заданной точностью, для чего вычисление по формуле метода рекомендуется проводить многократно, каждый раз уменьшая шаг интегрирования в 2 раза, пока разница между соседними приближениями не станет меньше заданной погрешности.

11.6 (5 б.) Метод прямоугольников. Вычислить определенный интеграл 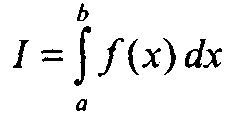методом прямоугольников:

, где п — количество отрезков разбиения; — значения функции на концах отрезков.

11.7 (5 б.) Метод трапеций. Вычислить определенный интеграл методом трапеций: , где п — количество отрезков разбиения; — значения функции на концах отрезков.

11.8 (6 б.) Метод Симпсона. Вычислить определенный интеграл по формуле Симпсона: где 2n — количество отрезков разбиения; — значения функции f(x) на концах отрезков.

11.9 (7 б.) Метод Эйлера. Найти приближенное решение обыкновенного дифференциального уравнения второго порядка у" = f(x,y,y') с заданными начальными условиями у(а)=у₀ и у'(0) = р₀ методом Эйлера на отрезке [а, b] с постоянным шагом h. Значения функции у(х) и ее производной р(х) = у' в узловых точках вычисляются по формулам:

11.10 (8 б.) Метод Ньютона. Составить таблицу значений функции у(х), которая задана неявно уравнением F(x,y) = 0. При фиксированном х уравнение F(x,y) = 0 можно решить методом Ньютона (см. задачу 11.2).

11.11 (5 б.) Линейная интерполяция. Функция у = f(*) задана таблично в массиве Y(n) при соответствующих значениях аргумента, хранящихся в неупорядоченном массиве Х(п), не содержащем одинаковых значений. Используя формулу линейной интерполяции:

построить таблицу значений функции на отрезке, содержащем все заданные значения аргумента, с постоянным заданным шагом h. Можно упорядочить пару массивов < Х(п), Y(n) > по возрастанию х.

11.12 (6 б.) Интерполяционный многочлен Лагранжа. Значения функции у=f(x)) заданы таблично в массиве Y(n) при соответствующих значениях аргумента в упорядоченном массиве Х{п). Найти значение функции в произвольной точке х по формуле Лагранжа:

11.13 (7 б.) Метод Рунге-Кутта. Найти приближенное решение обыкновенного дифференциального уравнения у' = f(x,y), у (а)=у₀ методом Рунге-Кутта пятого порядка на отрезке [а, b] с заданным постоянным шагом h. Значения функции у(х) в узловых точках вычисляются по формуле:

11.14 (76.) Метод золотого сечения. Найти минимум заданной функции у=f(x) на заданном отрезке [а, b] методом золотого сечения. Для этого на отрезке [а, b] находятся две точки:

Если f(x)> f(x₂), отбрасывается интервал [а,x], иначе — [х,b]; процесс продолжается до достижения за данной точности.

11.15 (6 6.) Метод парабол. Найти минимум заданной функции у = f{x), двигаясь от заданной точки х₀ по методу парабол:

пока не будет достигнута заданная точность.

11.16 (8 б.) Для заданной матрицы А(п,п) найти обратную Аиспользуя итерационную формулу:

где Е — единичная матрица;=Е. Итерационный процесс заканчивается, если для заданной погрешности справедливо