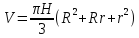- •К у р с о в а я р а б о т а
- •Глава 1. Теоретическое значение функций нескольких переменных
- •1. Основные теоретические сведения о функциях нескольких переменных
- •2. Значение функций нескольких переменных в прикладной математике.
- •3. Значение функций нескольких переменных в экономических областях
- •4. Значение функций нескольких переменных в других областях
- •Глава 2. Практическое значение функций нескольких переменных
- •1.Решение задач с помощью функций нескольких переменных в прикладной математике.
- •2.Решение задач с помощью функций нескольких переменных в экономических областях.
- •3.Решение задач с помощью функций нескольких переменных в других областях.
- •Список литературы и источников
Глава 1. Теоретическое значение функций нескольких переменных
1. Основные теоретические сведения о функциях нескольких переменных
Если
каждой паре  значений
двух независимых переменных величин
значений
двух независимых переменных величин  и
и  из
некоторой области их изменения
из
некоторой области их изменения 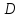 соответствует
определенное значение величины
соответствует
определенное значение величины 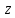 ,
то говорят, что
,
то говорят, что 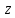 есть
функция
нескольких переменных
есть
функция
нескольких переменных 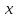 и
и 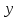 ,
определенная в области
,
определенная в области 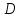 и
обозначают
и
обозначают
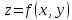 .
.
Совокупность
пар
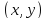 значений
значений
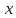 и
и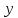 ,
при которых определена функция
,
при которых определена функция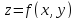 называетсяобластью
определения
или областью существования функции.
При
аналитическом способе задания функции,
т.е. с помощью некоторого аналитического
выражения, под областью определения
функции понимают множество всех значений
независимых переменных, при которых
это выражение имеет смысл.
называетсяобластью
определения
или областью существования функции.
При
аналитическом способе задания функции,
т.е. с помощью некоторого аналитического
выражения, под областью определения
функции понимают множество всех значений
независимых переменных, при которых
это выражение имеет смысл.
Окрестностью
точки
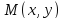 радиуса
радиуса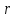 называется совокупность всех точек
называется совокупность всех точек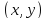 ,
которые удовлетворяют условию
,
которые удовлетворяют условию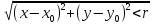
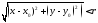 .
.
Число
 называетсяпределом
функции
называетсяпределом
функции
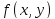 при стремлении точки
при стремлении точки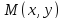 к
точке
к
точке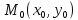 , если для каждого числа
, если для каждого числа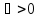 найдётся такое число
найдётся такое число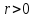 ,
что для любой точки
,
что для любой точки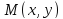 ,
для которых верно условие
,
для которых верно условие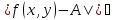 записывают
записывают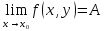 .
.
Точка
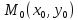 называется точкойминимума
функции
называется точкойминимума
функции
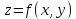 ,
если существует такое положительное
число, что из условия
,
если существует такое положительное
число, что из условия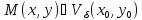 следует
следует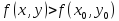 .
.
Точка
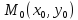 называется
точкой
максимума
функции
называется
точкой
максимума
функции
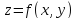 ,
если существует такое положительное
число, что из условия
,
если существует такое положительное
число, что из условия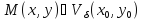 следует:
следует: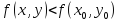 .
.
Точки минимума и максимума называются точками экстремума.
Функция
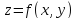 называется
непрерывной
в точке
называется
непрерывной
в точке
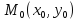 ,
если
,
если
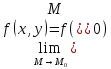
2. Значение функций нескольких переменных в прикладной математике.
Исследование прикладных задач обычно начинается ϲ построения и анализа простейшей, наиболее грубой математической модели рассматриваемого объекта. Под математической моделью будем понимать описание в виде ФНП реальных физических, химических, технологических, биологических, экономических и других процеϲϲов. Для того чтобы использовать математические методы для анализа и синтеза различных процессов, необходимо уметь опиϲать эти процеϲϲы на языке математики, то есть найти закономерность между величинами.
как описывается в научной литературе,
стоит отметить и следующий факт: с течением времени взгляды многих ученых меняются в сторону глобалистических тенденций,
как отмечают многие ученые, аналогичные ситуации могут возникать относительно часто и вызывать в свою очередь соответствующие проблемы,
взаимодополнение и взаимозаменяемость – неотделимая сущность соответствующих процессов,
можно отметить следующие моменты,
Методы отыϲкания экϲтремума функции многих переменных ϲ различными ограничениями часто называются методами математичеϲкого программирования. Задачи математического программирования – одни из важных оптимизационных задач, цель которых состоит в нахождении наилучшего (оптимального) ϲ точки зрения некоторого критерия или критериев варианта использования имеющихся ресурсов (труда, капитала и пр.), называются оптимизационными.
Это свидетельствует о том, что основным механизмом первичных объединений выступала регламентирована форма обеспечения "общение " разных племен и народов, которая в то время выступала мощным фактором становления глобальных форм сосуществования. Итак, учитывая исторический контекст данного явления и исходя из современных глобализационных реалий, методологически правильным является поставить вопрос о становлении новой формы социальной организации - глобальное общество.
Применение
ФНП нашлось и в физике. Так, например,
объем 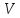 кругового цилиндра есть функция от
радиуса
кругового цилиндра есть функция от
радиуса
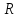 его
основания и от высоты
его
основания и от высоты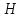 ; зависимость
между этими переменными выражается
формулой, которая дает возможность,
зная значения независимых переменных
; зависимость
между этими переменными выражается
формулой, которая дает возможность,
зная значения независимых переменных
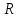 и
и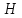 , установить
соответствующее значение
, установить
соответствующее значение 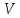 .
.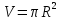 .
.
Объём
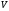 усечённого конуса является функцией
от трёх независимых переменных –
радиусов
усечённого конуса является функцией
от трёх независимых переменных –
радиусов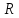 и
и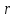 ,
и обоих его оснований, и высоты
,
и обоих его оснований, и высоты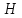 .
Он находится по формуле
.
Он находится по формуле