
- •14.1. З історії поняття функції
- •14.2. Числова функція
- •14.3. Графік функції
- •2. Ще одним перетворенням є розтяг уздовж осі Oy з коефіцієнтом k, що задається формулами:
- •Для побудови графіка функції потрібно розтягти графік функції у k раз уздовж осі ординат.
- •3. Паралельне перенесення вздовж осі абсцис на вектор (a; 0) задається формулами:
- •14.7. Періодичні функції
- •Необхідна умова екстремуму. Якщо точка x0 є точкою екстремуму функції і в цій точці існує похідна , то вона дорівнює нулю: .
Необхідна умова екстремуму. Якщо точка x0 є точкою екстремуму функції і в цій точці існує похідна , то вона дорівнює нулю: .
Зауважимо,
що теорема Ферма є лише необхідною
умовою екстремуму: з того, що похідна в
точці![]() перетворюється на нуль, ще не випливає,
що в цій точці функція має екстремум.
Наприклад, похідна функції
перетворюється на нуль, ще не випливає,
що в цій точці функція має екстремум.
Наприклад, похідна функції
![]() перетворюється на нуль у точці 0, але
екстремуму в цій точці функція не має
(рис. 3).
перетворюється на нуль у точці 0, але
екстремуму в цій точці функція не має
(рис. 3).

Рис. 3
Досі
ми розглядали критичні точки, в яких
похідна дорівнює нулю. Розглянемо тепер
критичні точки, в яких похідна не існує.
(Зазначимо, що, наприклад, точка 0 для
функції
![]() не є критичною: у ній похідна не існує,
але ця точка не є внутрішньою точкою
області визначення.) У цих точках функція
також може мати екстремум або не мати
його.
не є критичною: у ній похідна не існує,
але ця точка не є внутрішньою точкою
області визначення.) У цих точках функція
також може мати екстремум або не мати
його.
З теореми Ферма випливає, що при знаходженні точок екстремуму функції потрібно передусім знайти її критичні точки. Але, як випливає з розглянутих прикладів, питання про те, чи справді дана критична точка є точкою екстремуму, потребує додаткового дослідження. При цьому часто допомагають такі достатні умови існування екстремуму в точці.
Ознака
максимуму функції.
Якщо функція
![]() неперервна в точці
неперервна в точці
![]() і при цьому
і при цьому
![]() на інтервалі
на інтервалі
![]() і
і
![]() на інтервалі
на інтервалі
![]() ,
то точка
,
то точка
![]() є точкою максимуму функції
є точкою максимуму функції
![]() .
.
Зручно користуватися спрощеним формулюванням цієї ознаки.
Якщо
в точці
![]() похідна змінює знак із «плюса» на
«мінус», то
похідна змінює знак із «плюса» на
«мінус», то
![]() є
точкою максимуму.
є
точкою максимуму.
Ознака
мінімуму функції.
Якщо функція
![]() неперервна в точці
неперервна в точці
![]() і при цьому
і при цьому
![]() на інтервалі
на інтервалі
![]() і
і
![]() на інтервалі
на інтервалі
![]() ,
то точка
,
то точка
![]() є точкою мінімуму функції
є точкою мінімуму функції
![]() .
.
Зручно користатися спрощеним формулюванням цієї ознаки.
Якщо
в точці
![]() похідна змінює знак із «мінуса» на
«плюс», то
похідна змінює знак із «мінуса» на
«плюс», то
![]() є точкою мінімуму.
є точкою мінімуму.
Приклад.
Знайти точки екстремуму функції
![]() .
.
-
Похідна цієї функції дорівнює
 ,
визначена в усіх точках і перетворюється
на нуль у точках –1 і 1. У точці –1 похідна
змінює знак із «мінуса» на «плюс» (
,
визначена в усіх точках і перетворюється
на нуль у точках –1 і 1. У точці –1 похідна
змінює знак із «мінуса» на «плюс» ( при
при
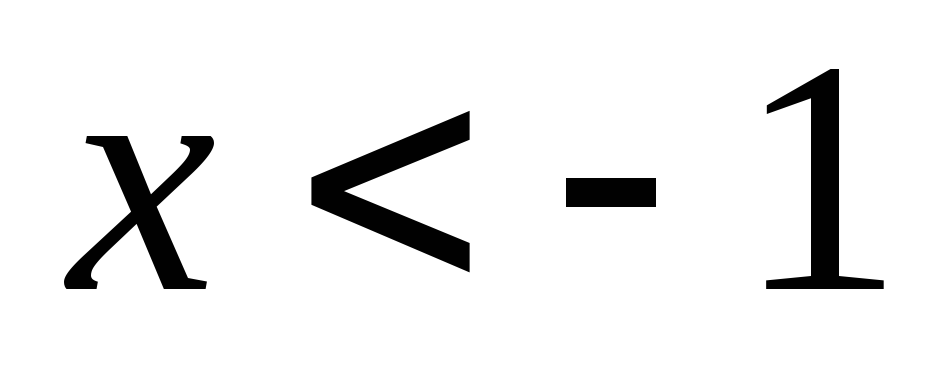 і
і
 при
при
 ).
У точці 1 похідна змінює знак із «плюса»
на «мінус». Користаючись ознаками
максимуму і мінімуму, дістаємо, що точка
–1 є точкою мінімуму, а точка 1 — точкою
максимуму функції
).
У точці 1 похідна змінює знак із «плюса»
на «мінус». Користаючись ознаками
максимуму і мінімуму, дістаємо, що точка
–1 є точкою мінімуму, а точка 1 — точкою
максимуму функції
 .
Графік функції зображено на рис. 4.
.
Графік функції зображено на рис. 4.
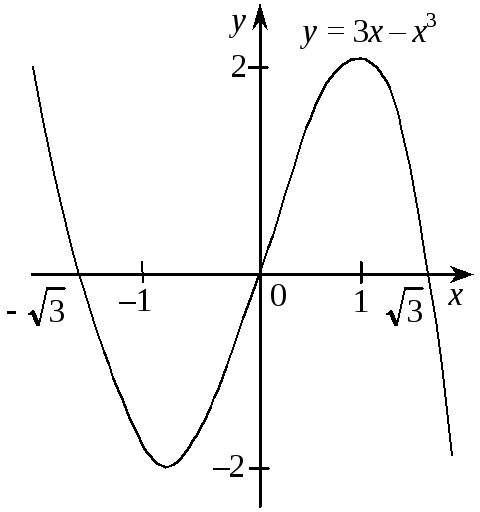
Рис. 4
![]()
1. Знайти критичні точки функції, графік якої зображено на рис. 1 і 2.

Рис. 1
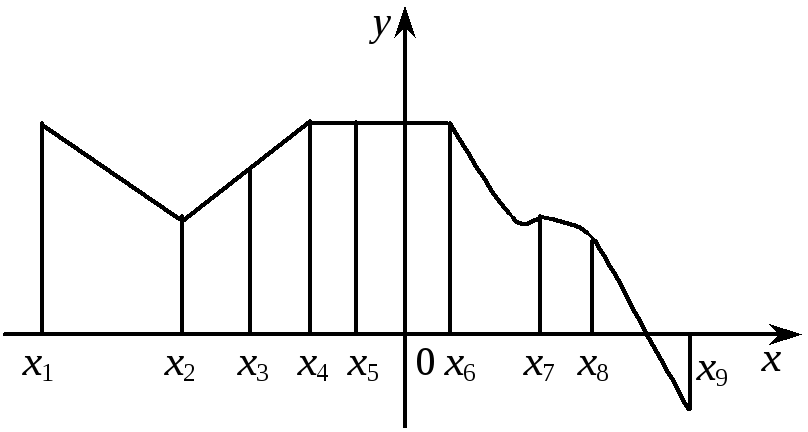
Рис. 2
2. Знайти критичні точки функції.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
3. Знайти критичні точки функції. Визначити, які з них є точками максимуму, а які — точками мінімуму.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
4. Довести,
що функція
![]() не має критичних точок.
не має критичних точок.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Знайти
критичні точки функції
![]() (5—6).
(5—6).
5. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
6. б)
![]()
а)

в)
![]() ;
;
г)

7. Дослідити функцію на зростання, спадання та екстремум. Побудувати її графік.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
