14.7. Періодичні функції

Багато процесів і явищ, з якими ми стикаємося на практиці, мають повторюваний характер. Так, взаємне розміщення Сонця та Землі повторюється раз на рік. Положення маятника в моменти часу, що відрізняються на період його коливання, однакові.

Такого роду процеси називають періодичними, а функції, що їх описують, — періодичними функціями.

Відомі нам основні тригонометричні функції — періодичні. Так, для будь-якого числа x і кожного цілого k виконується рівність . Звідси випливає, що — період функ­ції синус ( — довільне ціле число).

Загалом, говорячи про періодичність функції f, стверджують, що існує таке число , що область визначення разом з кожною точкою x містить і точки, утворювані з точки x паралель­ним перенесенням уздовж осі Ox (праворуч і ліворуч) на відстань T.

Функцію f називають періодичною з періодом , якщо для будь-якого x з області визначення цієї функції її значення в точках x, x – T і x + T рівні між собою, тобто .

Оскільки функції синус і косинус визначені на всій числовій прямій і , для кожного , синус і косинус — періодичні функції з періодом .

Тангенс і котангенс — періодичні функції з періодом . Справді, області визначення цих функцій разом із кожним містять числа й і справджуються рівності: , .

Очевидно, що коли функція f періодична з періодом T, то при будь-якому цілому число також є періодом цієї функції. Наприклад, при , скориставшись кілька разів означенням періодичної функції, знаходимо:

Варто запам’ятати, що:

а) найменший додатний період функцій і дорівнює ;

б) найменшим додатним періодом функцій і є число .

Періодичністю основних тригонометричних функцій ми вже фактично користувалися раніше при побудові графіків. Справджується таке твердження:

Для побудови графіка періодичної функції з періодом достатньо побудувати на відрізку завдовжки , а далі здобутий графік паралельно перенести на відстань праворуч і ліворуч уздовж осі (рис. 1), де — будь-яке натуральне число).

Рис. 1

Приклад. Побудувати графік функції .

• Для побудови скористаємося тим, що функція 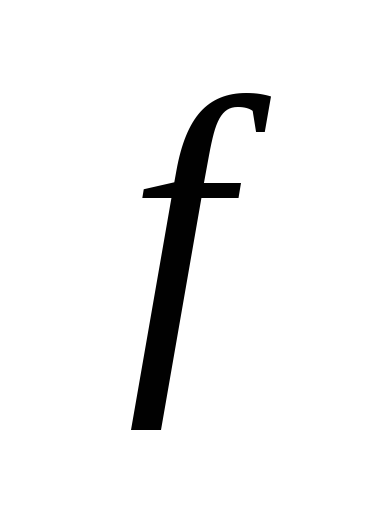періодична з періодом . Справді, функція визначена на всій прямій, і, отже, область її визначення разом з довільною точкою містить точки, утворювані з паралельними перенесеннями вздовж осі праворуч і ліворуч на . Крім того, унаслідок періодичності косинуса . Корис­ту­ючись властивістю графіків періодичних функцій, будуємо графік 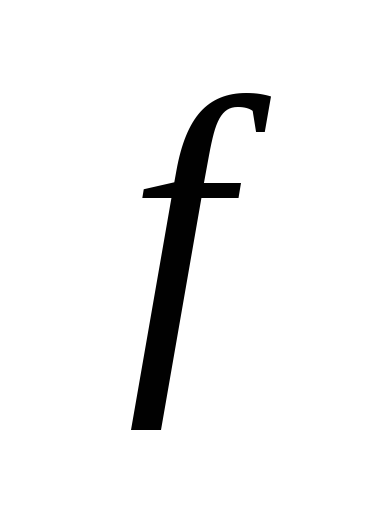спочатку на відрізку (для цього згідно з відомими правилами перетворення графіків розтягуємо графік косинуса вздовж осі 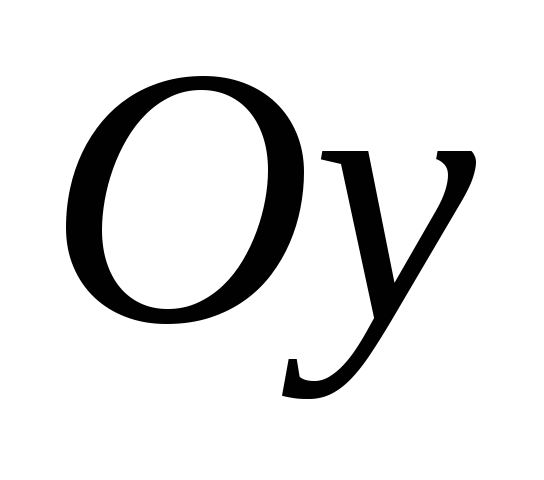в 2 рази і переносимо його на одну одиницю вгору (рис. 2), а потім за допомогою паралельного перенесення продов­жуємо його на всю числову пряму (рис. 3).

Рис. 2

Рис. 3

Приклад. Довести, що функція періодична і її найменший додатний період дорівнює .

• Тангенс визначений при всіх значеннях аргументу, що не дорів­нюють , . Тому область визначення даної функції складається з таких , що , тобто 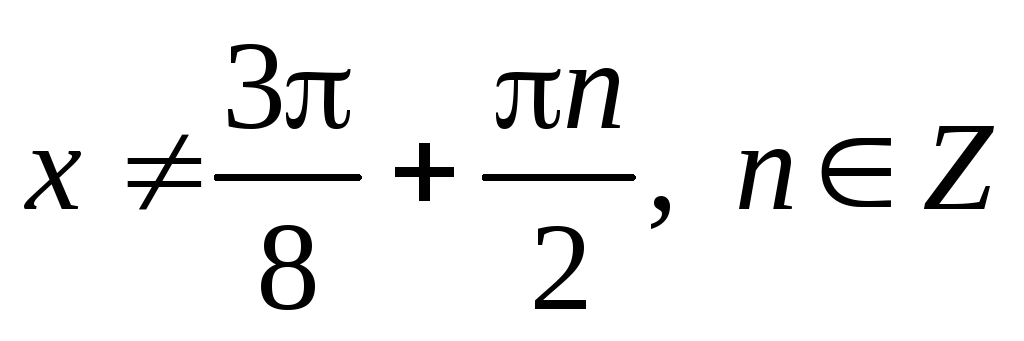. Звідси випливає, що поряд з довільною містить і всі точ­ки виду , . Очевидно, що число є періодом , оскільки . Зали­шається довести, що число 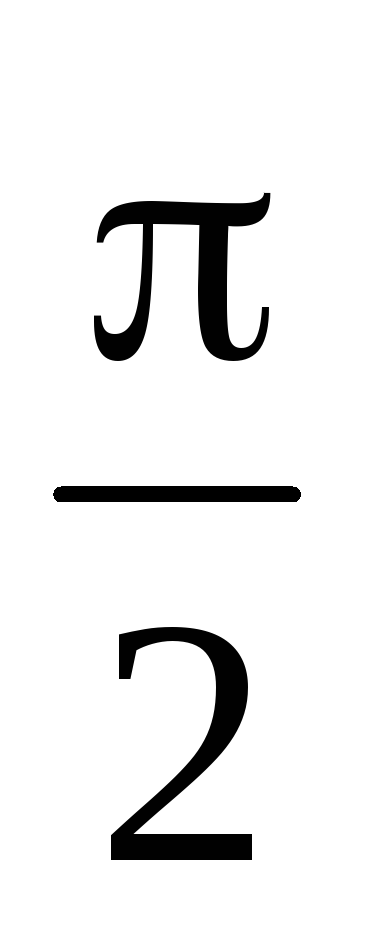— найменший додатний період 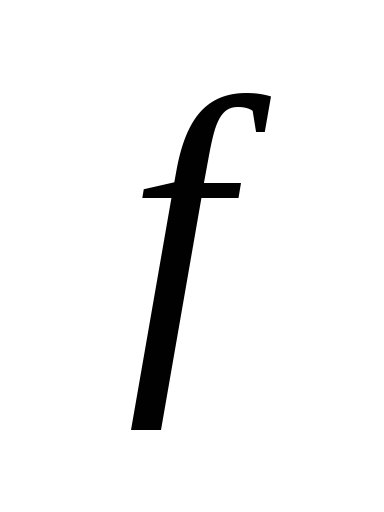. Припустимо, що періодом 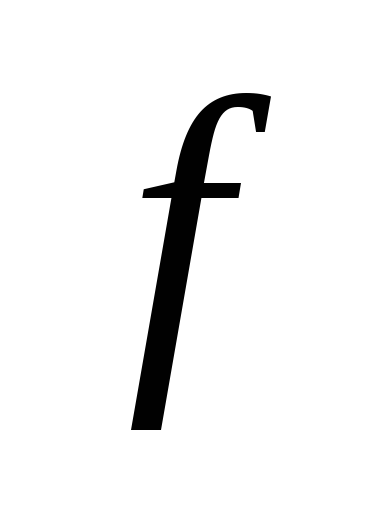є таке число , що . Тоді для будь-якого справджується рівність

,

оскільки — період . Але це означає, що — період функції . За припущенням , тобто . Маємо суперечність із доведеним раніше: найменший додатний період тангенса дорівнює . 

Аналогічно доводиться загальне твердження:

Якщо функція періодична і має період , то функція , де і — сталі, а , також періодична, причому її період дорівнює .

Із цього твердження відразу дістаємо, що, наприклад, періодом функції є число , а період функції дорівнює .

1. Довести, що наведені далі функції парні.

а) ; б) ;

в) ; г) .

д) ; е) ;

є) ; ж) .

2. Довести, що наведені далі функції непарні.

а) ; б) ;

в) ; г) .

д) ; е) ;

є) ; ж) .

3. Довести, що число є періодом функції

а) ; б) ;

в) ; г) .

4. Довести, що функція періодична.

а) ; б) ;

в) ; г) .

5. Знайти найменший додатний період кожної з наведених далі функцій.

а) ;

б) ;

в) ;

г) .

6. Знайти найменший додатний період і побудувати графік функції.

а) ; б) ;

в) ; г) .

7. З’ясувати, яка з наведених далі функцій парна, яка непарна, а яка ні парна, ні непарна.

а) ; б) ;

в) ; г) .

д) ; е) ;

є) ; ж) .

8. Побудувати графік функції.

а) ; б) ;

в) ; г) .

9. Довести, що число 2 не є періодом функції.

а) ; б) ;

в) ; г) .

14.7. Зростання та спадання функцій

Функція зростає на множині , якщо для будь-яких x₁ і x₂ з множині , таких що виконується нерівність .

Функція спадає на множині , якщо для будь-яких x₁ і x₂ з множині , таких що, виконується нерівність .

Іншими словами, функція називається зростаючою на множині , якщо більшому значенню аргументу з цієї множині відповідає більше значення функції. Функція називається спад­ною на множині , якщо більшому значенню аргументу відповідає менше значення функції.

14.8. Екстремуми

Околом точки а називається будь-який інтервал, що містить цю точку. Наприклад, інтервал (2; 6) — один з околів точки 3, інтервал (– 3,3; – 2,7) — окіл точки – 3.

Точка x₀ називається точкою мінімуму функції f, якщо для всіх x з деякого околу x₀ виконується нерівність (рис. 1, а, б).

Точка x₀ називається точкою максимуму функції f, якщо для всіх x з деякого околу x₀ виконується нерівність (рис. 2, а, б).

За означенням у точці максимуму значення функції найбільше з-поміж усіх її значень з деякого околу цієї точки, тому графік функції в околі , як правило, має вигляд гладенького пагорба (див. рис. 2, а і рис. 3 — точки x₁, x₂, x₃) або піка (див. рис. 2, б). В околі точки мінімуму графіки, як правило, зображуються у вигляді западини — гладенької (рис. 1, б і рис. 3 — точки x₄, x₅), або загостреної (див. рис. 1, а і рис. 3 — точка x₆).

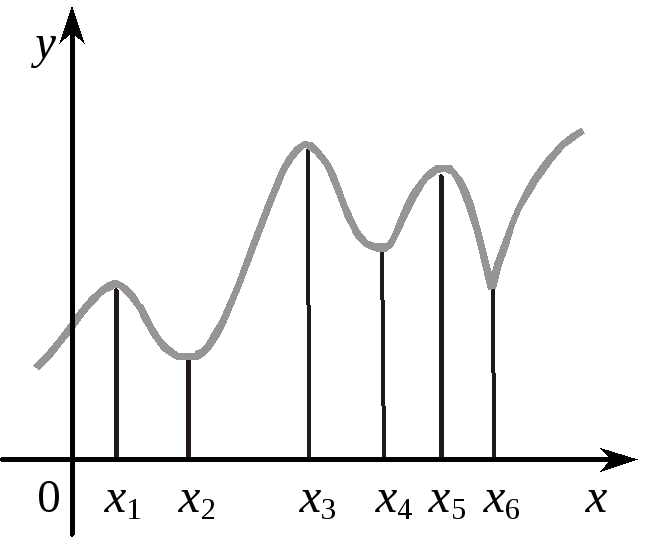
Рис. 3

Для точок максимуму і мінімуму функції існує спільна назва — їх називають точками екстремуму. Значення функції в цих точках називають відповідно максимумами і мінімумами функції (спільна назва — екстремум функції). Точки максимуму позначають x_max, а точки мінімуму — x_min. Значення функції в цих точках позначаються відповідно y_max і y_min.

1. Для функцій, графіки яких зображено на рисунку, знайти:

а) проміжки зростання та спадання функції;

б) точки максимуму і мінімуму функції;

в) екстремуми функції.

Знайти проміжки зростання та спадання, точки максимуму і точки мінімуму функції, її максимуми і мінімуми (2—5).

2. а) ; б) ;

в) ; г) .

3. а) ; б) ;

в) ; г) .

4. а) ; б) ;

в) ; г) .

5. а) ; б) ;

в) ; г) .

Знайти проміжки зростання та спадання, точки екстремуму і екстремуми функції (6—7).

6. а) ; б) ;

в) ; г) .

7. а) ; б) ;

в) ; г) .

14.9. Дослідження функцій

1. Побудова графіків функцій. У шкільному курсі математики графіки функцій будували за точками. У багатьох випадках цей метод дає добрі результати, якщо, звичайно, відшукали достатньо велику кількість точок. Однак при цьому доводиться складати великі таблиці значень функції, а головне, можна не помітити істотних особливостей функції і через це помилитися при побудові графіка.

Для того щоб уникнути помилок, потрібно навчитися виявляти характерні особливості функції під час її дослідження.

2. Схема дослідження функцій. У загальному випадку дослідження складається з таких кроків:

1) знайти область визначення і область значень даної функції f;

2) з’ясувати, чи має функція особливості, що полегшують дослідження, тобто чи є функція f: а) парною чи непарною; б) періодичною;

3) обчислити координати точок перетину графіка з осями координат;

4) знайти проміжки знакосталості функції f;

5) з’ясувати, на яких проміжках функція f зростає, а на яких спадає;

6) знайти точки екстремуму, вид екстремуму (максимум чи мінімум) і обчислити значення f у цих точках;

7) дослідити поводження функції f в околі характерних точок, що не входять в область визначення (наприклад, точка x = 0 для функції ), і при великих (за модулем) значеннях аргументу.

Вертикальні прямі, до яких необмежено наближається графік функції f (наприклад, пряма x = 0 для , називають вертикальними асимптотами.

Найчастіше графік має вертикальну асимптоту x = a у разі, коли вираз, що задає функцію, має вигляд дробу, знаменник якого перетворюється на нуль у точці a. Наприклад, для графіка функції вертикальними асимптотами є прямі , де .

Якщо графік функції необмежено наближається до деякої горизонтальної (для функції це пряма ) або похилої (пряма для графіка функції ) прямої при необмеженому зростанні (за модулем) x, то таку пряму називають горизонтальною (відповідно похилою) асимптотою.

3. «Читання» графіків. У більшості прикладів і задач на побудову графіків функцій ви стикалися з такою ситуацією: функцію f задано формулою, потрібно дослідити її властивості та побудувати графік. Значний практичний інтерес становить інша задача: задано графік f, за допомогою якого потрібно встановити основні властивості цієї функції.

Такі задачі часто постають під час експериментальних досліджень. Побудову графіків при цьому виконують різними методами. Наприклад, за точками, знайденими експери­ментально. Існують також численні самописні прилади, скажімо осцилографи, на екранах яких електричні коливання перетворюються в наочні графічні зображення. Іншим прикладом приладу, що дає змогу діставати наочний графічний опис, є кардіограф. Вивчаючи здобуту за його допомогою кардіограму, лікарі роблять висновки про стан серцевої діяльності.

Із доволі типовим прикладом труднощів, що постають при дослідженні реальних процесів, для опису яких ще не створено точ­них теорій, можна ознайомитися, розглянувши такий рисунок.

Маємо графіки середньодобового ходу температур по Київській області в лютому 1994 року. Жирною лінією зображено теоретичні криві А та Б, що фіксують результати довгострокового прогнозу (оскільки прогноз подається з точністю до 5 С, кривих дві). Читаючи цей графік, встановлюємо, наприклад, що передбачалися три «хвилі холоду» (у період з 4 по 10, з 17 по 19 і з 23 по 26 лютого). Передбачалося також, що не буде відлиг і переважатиме в цілому холодна (–17 … –22 С) погода. Проте насправді (графік фактичного ходу температур зображено тонкою лінією В) температура була вищою за норму на 5—10 С (кліматичну норму, що є результатом багаторічних спостережень, подано лінією Г), у період з 4 по 8 лютого було потепління, а не похолодання. Ці та інші відомості про прогноз і реальну картину ви можете дістати, читаючи графіки, наведені на рисунку.

1. Дослідити за загальною схемою функцію, задану графіком (рис. 1—4).

Дослідити за загальною схемою функцію та побудувати її графік (2—4).

2. а) ; б) ;

в) ; г) .

3. а) ; б) ;

в) ; г) .

4. а) ; б) ;

в) ; г) .

14.10. Ознаки зростання та спадання функції

Одне з основних завдань дослідження функції полягає у знаходженні проміжків її зростання та спадання. Таке дослідження легко виконати за допомогою похідної. Сформулюємо відповідні твердження.

Достатня ознака зростання функції. Якщо в кож­ній точці інтервалу I, то функція зростає на I.

Достатня ознака спадання функції. Якщо в кожній точці інтервалу I, то функція спадає на I.

Приклад 3. Знайти проміжки зростання (спадання) функції

• Функцію визначено на всій числовій прямій. Похідна її така:

Оскільки , легко дістаємо, що для всіх дійс­них . Це означає, що функція спадає на всій числовій прямій.

Знайти проміжки зростання та спадання функцій (1—3).

1. а) ; б) ;

в) ; г) .

2. а) ; б) ;

в) ; г) .

3. ; б) ;

в) ; г) .

Знайти проміжки зростання та спадання функції і побудуйте її графік (4—5).

4. а) ; б) ;

в) ; г) .

5. а) ; б) ;

в) ; г) .

6. Довести, що функція f зростає на R, а функція спадає на R.

а) ; б) ;

в) ; г) .

7. Довести, що рівняння має єдиний корінь на кожному з даних проміжків P₁ і P₂.

а) ;

б) ;

в) ;

г) .

14.11. Критичні точки функції, максимуми і мінімуми

Внутрішні точки області визначення функції, в яких її похідна дорівнює нулю або не існує, називаються критичними точками цієї функції. Ці точки відіграють важливу роль при побудові графіка функції, оскільки тільки вони можуть бути точками екстре­муму функції (рис. 1 і 2). Сформулюємо відповідне твердження, його називають теоремою Ферма (на честь французького математика П. Ферма).