2. Ще одним перетворенням є розтяг уздовж осі Oy з коефіцієнтом k, що задається формулами:

(1)

Щоб побудувати точку , в яку переходить дана точка M при розтягу, потрібно побудувати на прямій АМ, де А — проекція М на вісь Ox (рис. 3), точку, гомотетичну М щодо центра А (коефіцієнт гомотетії дорівнює коефіцієнту k розтягу). На рис. 4 зоб­ражено побудову точок, в які переходять дані точки в результаті розтягу з коефіцієнтами і –2.

Рис. 3

Рис. 4

З’ясуємо, в яку фігуру переходить графік функції f при розтягу. З формул (2) відразу дістаємо, що довільна точка графіка f переходить у точку. Звідси випливає, що графік f переходить у фігуру, що складається з усіх точок, де . Ця фігура є графіком функції . Доведемо таке правило.

Для побудови графіка функції потрібно розтягти графік функції у k раз уздовж осі ординат.

Приклад. Побудувати графіки функцій y = –2 x² і

• Побудова в першому випадку виконується на основі графіка функції y = x² (рис. 5), а в другому випадку спочатку будуємо графік функції , а далі виконуємо розтяг уздовж осі ординат з коефіцієнтом (рис. 6).

Зауваження. Якщо то розтяг з коефіцієнтом k часто називають стиском. Наприклад, розтяг з коефіцієнтом називають стиском удвічі. Зазначимо також, що коли те для побудови графіка функції потрібно спочатку розтягти графік f у раз, а потім відбити його симетрично відносно осі абсцис (див. рис. 5).

Рис. 5

Рис. 6

3. Паралельне перенесення вздовж осі абсцис на вектор (a; 0) задається формулами:

(3)

Кожна точка графіка функції f переходить відповідно згідно з формулами (2) переходить у точку (x + a; f (x)). Тому за допомогою змінних , можна записати, що графік f пере­ходить у фігуру Ф, що складається з точок де набуває всіх значень виду x + a (x пробігає D(f)).

Саме при цих значеннях число x – a належить D(f) і значення визначене. Отже, фігура Ф є графіком функції y = = f (x – a). Отже, маємо висновок.

Графік функції y = f (x – a) виходить із графіка f переносом (уздовж осі абсцис) на вектор (a; 0).

Зауважимо: якщо , то вектор (a; 0) напрямлений у додатному напрямку осі абсцис, а при — у від’ємному.

Приклад. Побудову графіків функцій і ілюструють рис. 7 і 8.

Рис. 7

Рис. 8

4. Розтяг уздовж осі Ох із коефіцієнтом k задається формулами:

(4)

Довільна точка графіка функції f переходить при такому розтягу в точку (kx; f (x)). Переходячи до змінних , , можна записати, що графік y = f (x) переходить у фігуру, що складається з точок де набуває всіх значень виду , а .

Ця фігура є графіком функції . Отже, доходимо висновку.

Для побудови графіка функції потрібно виконати розтяг графіка функції f з коефіцієнтом k уздовж осі абсцис.

Приклад. Побудову графіків функцій і ілюструють рис. 9 і 10.

Рис. 9

Рис. 10

14.5. Відображення

Функцію з областю визначення D і областю значень E називають також відображенням множини D на множину E. Можна сказати, наприклад, що формула задає відображення множини R дійсних чисел на відрізок [–1; 1]. Терміни «функція» і «відображення» — синоніми.

Нерідко розглядають функції (відображення), область визначення чи область значень яких (а можливо, і обидві ці множини) не є числовими множинами.

Поняття відображення часто відносять до основних понять математики. За його допомогою можна дати таке означення функції:

Функцією з областю визначення D і областю значень E називається відображення множини D на множину E, при якому кожному елементу множини D відповідає один цілком визначений елемент множини E і кожний елемент множини E поставлено у відповідність хоча б одному елементу множини D.

1. Знайти значення функції.

а) у точках –1, , 10;

б) у точках , 0, ;

в) у точках 0, 1, 2;

г) у точках , 0,

2. Записати значення функції:

а) у точках х₀, ;

б) у точках а, ;

в) у точках х₀, ;

г) у точках

3. Чи є графіком функції фігура, зображена на (рис. 1—4)?

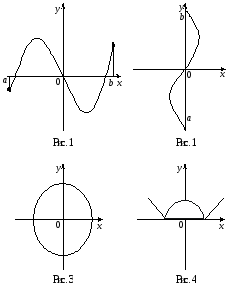
4. Знайти область визначення кожної з функцій.

а) ; б) ;

в) ; г) .

д) ; е) ;

є) ; ж) .

5. Знайти область визначення та область значень кожної з фун­кцій.

а) ; б) ;

в) ; г) .

6. Зобразити графік будь-якої функції f, заданої такими умовами:

а) ;

б) .

7. В одній і тій самій системі координат побудувати графіки функцій.

а) ;

б) ;

в) ;

г) .

Побудувати графіки функцій (8—9).

8. а) ; б) ;

в) ; г) .

9. а) ; б) ;

в) ; г) .

10. Знайти значення функції.

а) у точках –2; ; 0; 5;

б) у точках –2; –1; 0; 4;

в) у точках ; ; 0; .

11. Знайти область визначення функції.

а) ; б) ;

в) ; г) .

12. Побудувати графіки функцій.

а) ; б)

в) ; г)

д) ; е) ;

є) ; ж) .

14.6. Парні і непарні функції. Періодичність тригонометричних функцій

1. Парні і непарні функції. Розглянемо функції, області визначення яких симетричні відносно початку координат, тобто для будь-якого x з області визначення число –x також належить області визначення. Серед таких функцій виокремлюють парні і непарні.

Функція f називається парною, якщо для будь-якого x з її області визначення f (–x) = f (x) (рис. 1).

Рис. 1

Функція f називається непарною, якщо для будь-якого x з її області визначення f (–x) = –f (x) (рис. 2).

Рис. 2

Приклад. Функція парна, а функція непар­на. Справді, область визначення кожної з них (це вся числова пряма) симетрична відносно точки О, причому для будь-якого x виконуються рівності , . Графіки зазначених функцій зображено на рис. 3 і 4.

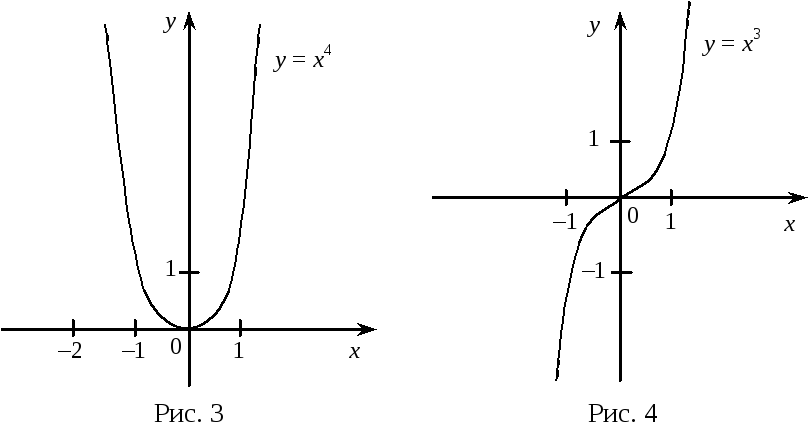
При побудові графіків парних і непарних функцій користуватимемося такими відомими з курсу алгебри властивостями:

1. Графік парної функції симетричний відносно осі ординат.

2. Графік непарної функції симетричний відносно початку координат.

Із цих двох правил випливає таке: при побудові графіка парної або непарної функції достатньо побудувати його частину для невід’ємних x, а потім відбити здобутий графік відносно осі ординат (у разі парної функції) або початку координат (у разі непарної).

Приклад. Функція непарна, її графік симетричний відносно початку координат (рис. 5).

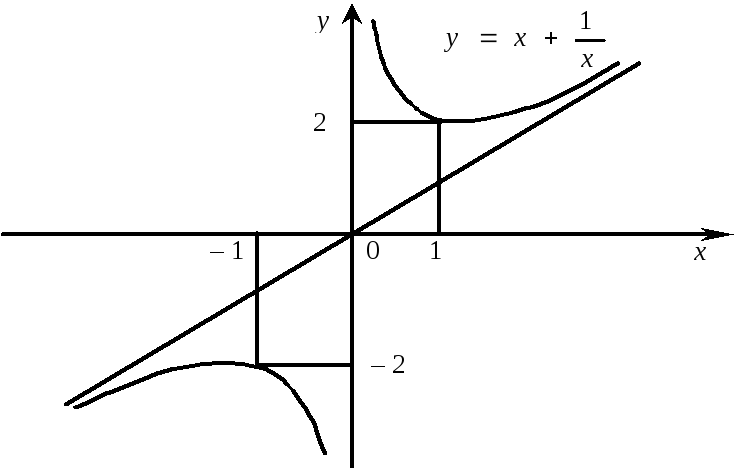
Рис. 5

Основні тригонометричні функції синус, тангенс і котангенс непарні, а косинус — парна функція. Тому графіки синуса, тангенса і котангенса симетричні відносно початку координат, а графік косинуса симетричний відносно осі ординат.

Приклад. Функція парна, оскільки область її визначення симетрична відносно точки x = 0 (вона складається з усіх чисел, відмінних від –1, 0 і 1) і для всіх виконується рівність

.

Графік цієї функції симетричний щодо осі Оy (рис. 6).

Рис. 6

Приклад. Функція є ні парною, ні непарною. Область її визначення симетрична відносно точки 0, але, наприклад, при не виконується ні рівність , ні рівність , оскільки , а .