
АиГ / тема 9
.docКурс “Алгебра и Геометрия”
(спец. прикладная математика, информатика, 1 курс, 1 семестр)
Тема 8. Прямая в пространстве. – 4 ч.
Содержание: прямая, как линия пересечения двух плоскостей; канонические и параметрические уравнения прямой.
Цель: изучить различные способы задания прямых в пространстве их уравнениями; научиться применять уравнения прямых при решении стереометрических задач.
Форма контроля: опрос.
Задачи
Задача 1 ([5], 982).
Составить уравнения прямых, образованных
пересечением плоскости
![]() с координатными плоскостями.
с координатными плоскостями.
Задача 2 ([5], 989).
В пучке плоскостей
![]() найти плоскость, которая:
найти плоскость, которая:
-
проходит через точку
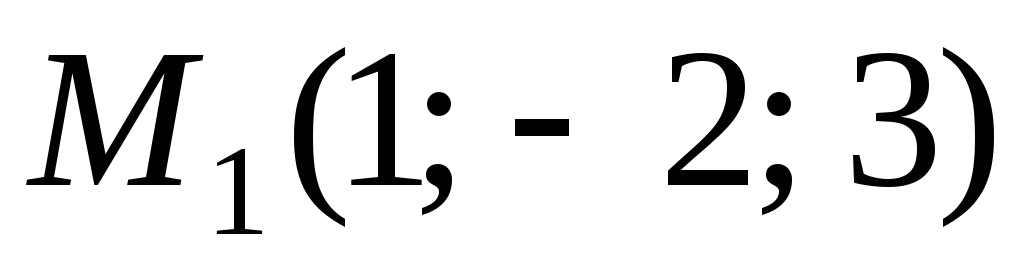 ;
; -
параллельна оси Ох;
-
параллельна оси Оу;
-
параллельна оси Оz.
Задача 3 ([5], 995).
Составить уравнение плоскости, которая
проходит через прямую пересечения двух
плоскостей
![]() и
и
![]() параллельно
отрезку, ограниченному точками
параллельно
отрезку, ограниченному точками
![]() и
и
![]() .
.
Задача 4 ([5], 996).
Написать уравнение плоскости, принадлежащей
пучку плоскостей
![]() и равноудаленной от точек
и равноудаленной от точек
![]() и
и
![]() .
.
Задача 5 ([5], 997).
Определить, принадлежит ли плоскость
![]() пучку
плоскостей
пучку
плоскостей
![]() .
.
Задача 6 ([5], 998).
Определить, принадлежит ли плоскость
![]() пучку
плоскостей
пучку
плоскостей
![]() .
.
Задача 7 ([5], 999).
Определить, при каких значениях
![]() и
и
![]() плоскость
плоскость
![]() принадлежит
пучку
плоскостей
принадлежит
пучку
плоскостей
![]() .
.
Задача 8 ([5], 1000).
Написать уравнение плоскости, которая
принадлежит пучку плоскостей
![]() и отстоит от начала координат на
расстоянии
и отстоит от начала координат на
расстоянии
![]() .
.
Задача 9 ([5], 1001).
Написать уравнение плоскости, которая
принадлежит пучку плоскостей
![]() и отстоит от точки
и отстоит от точки
![]() на расстоянии
на расстоянии
![]() .
.
Задача 10 ([5],
1002). Написать
уравнение плоскости, которая принадлежит
пучку плоскостей
![]() и отсекает от координатного угла Оху
треугольник
с площадью, равной 6 кв. ед.
и отсекает от координатного угла Оху
треугольник
с площадью, равной 6 кв. ед.
Задача 11 ([5], 1003). Составить уравнение плоскостей, проектирующих прямую
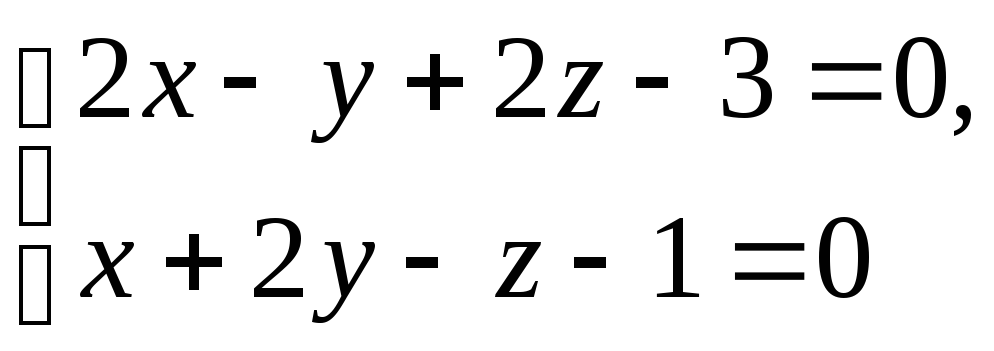
на координатные плоскости.
Задача 12 ([5], 1004). Составить уравнения проекции прямой
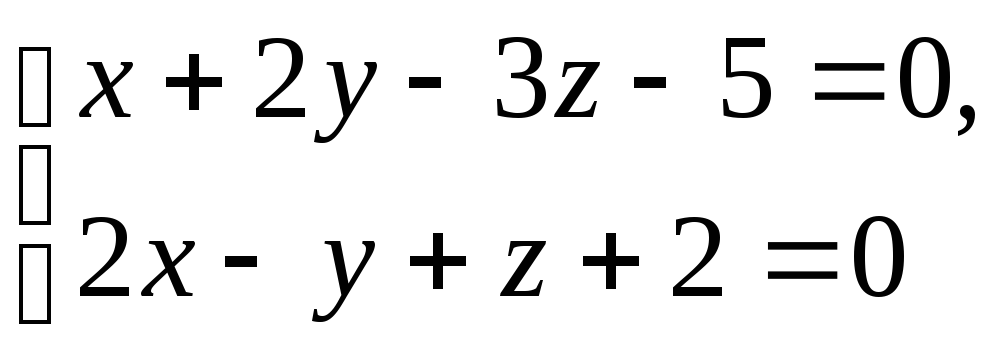
на координатные плоскости.
Задача 13 ([5], 1005). Составить уравнение плоскости, проектирующей прямую

на плоскость
![]() .
.
Задача 14 ([5], 1006). Составить уравнения проекции прямой
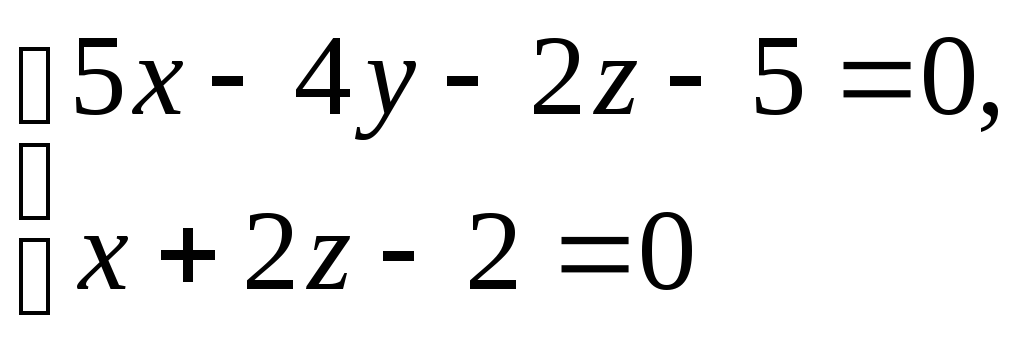
на плоскость
![]() .
.
Задача 15 ([5], 1020). Составить параметрические уравнения следующих прямых
1)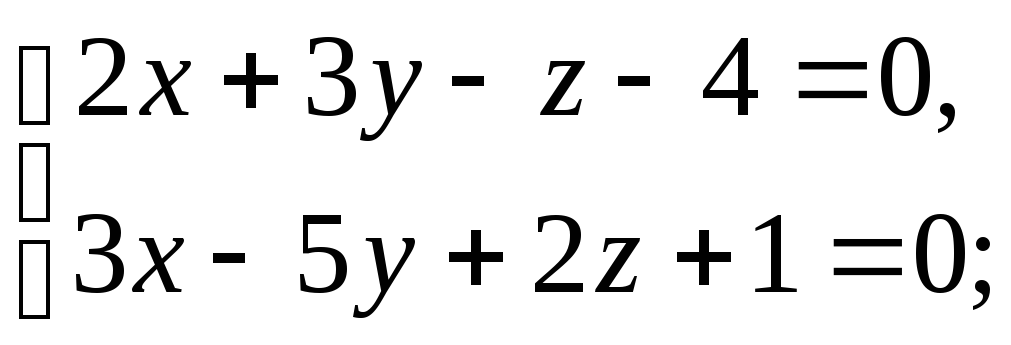 2)
2)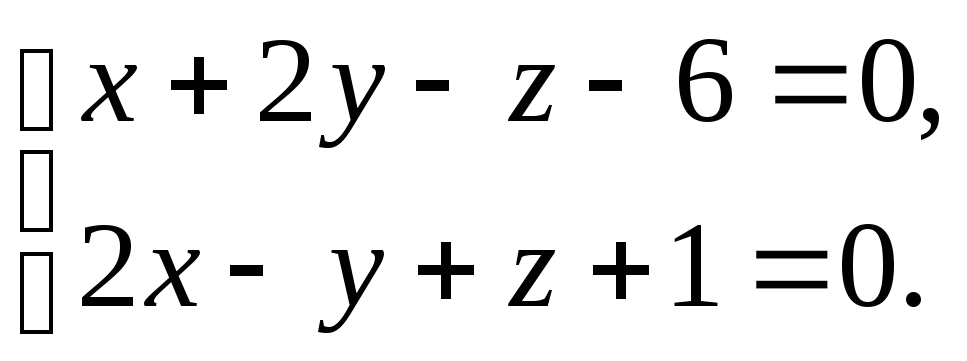
Задача 16 ([5], 1021). Доказать параллельность прямых:
1)
![]() и
и

2)
![]() и
и
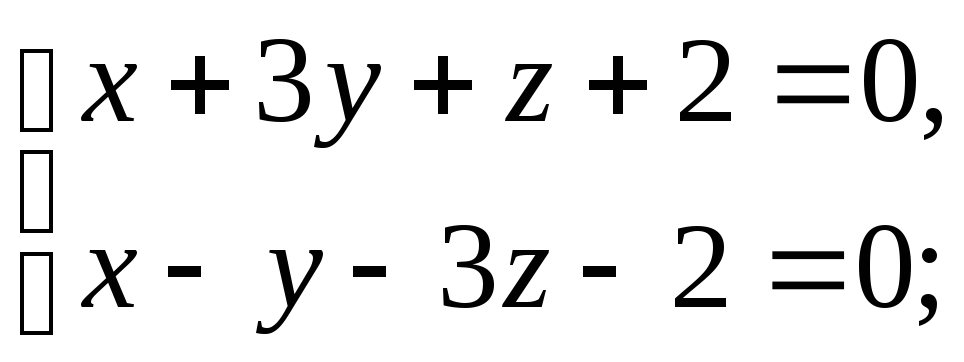
3)
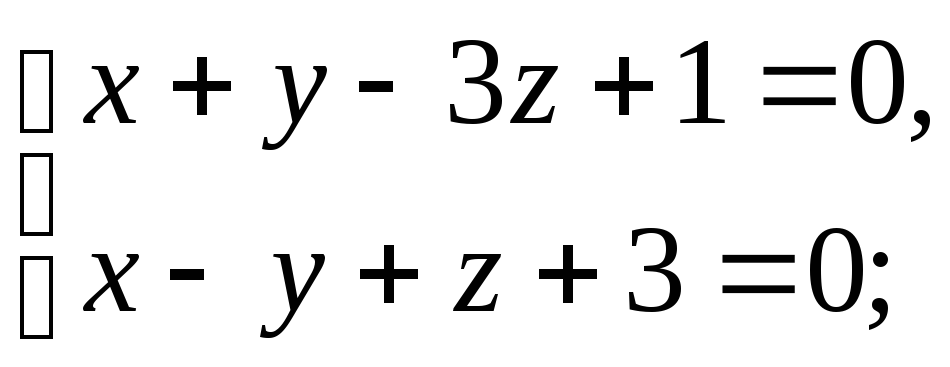 и
и

Задача 17 ([5], 1023). Найти острый угол между прямыми
![]() и
и
![]()
Задача 18 ([5],
1024). Найти
тупой угол между прямыми
![]() и
и
![]()
Задача 19 ([5], 1025). Определить косинус угла между прямыми:
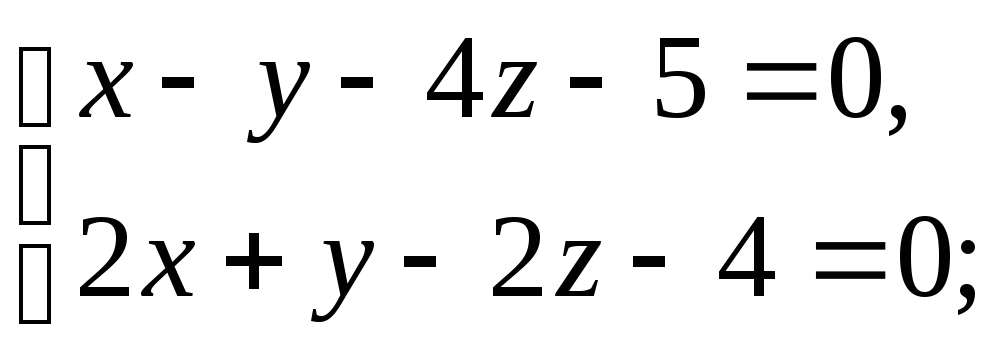 и
и

Задача 20 ([5],
1026). Доказать,
что прямые заданные параметрическими
уравнениями
![]() и
и
![]() ,
пересекаются.
,
пересекаются.
Задача 21 ([5], 1027). Даны прямые
![]() и
и
![]() ,
,
при каком значении
![]() они пересекаются?
они пересекаются?
Задача 22 ([5],
1029). Составить
уравнение прямой, которая проходит
через точку
![]() перпендикулярно к вектору
перпендикулярно к вектору
![]() и пересекает прямую
и пересекает прямую
![]() .
.
Задача 23 ([5],
1030). Составить
уравнение прямой, которая проходит
через точку
![]() и пересекает две прямые
и пересекает две прямые
![]() и
и
![]() .
.
Задача 24 ([5], 1031). Составить параметрические уравнения общего перпендикуляра двух прямых, заданных уравнениями
![]() и
и
![]()
Задача 25 ([5],
1032). Даны
уравнения движения точки
![]()
![]() .
Определить её скорость
.
Определить её скорость
![]() .
.
Задача 26 ([5],
1033). Даны
уравнения движения точки
![]()
![]() .
Определить расстояние
.
Определить расстояние
![]() ,
за промежуток времени от
,
за промежуток времени от
![]() до
до
![]() .
.
Задача 27 ([5],
1034). Составить
уравнения движения точки
![]() ,
которая, имея начальное положение
,
которая, имея начальное положение
![]() ,
движется прямолинейно и равномерно в
направлении вектора
,
движется прямолинейно и равномерно в
направлении вектора
![]() со скоростью
со скоростью
![]() .
.
Тема 9. Прямая в пространстве.
Ответы
Задача 1.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Задача 2.
![]()
1)
![]()
2)
![]()
3)
![]()
4)
![]()
Задача 3.
![]()
Задача 4.
![]() ,
,
![]() .
.
Задача 5. Принадлежит.
Задача 6. Не принадлежит.
Задача 7.
![]() ,
,
![]() .
.
Задача 8.
![]() ,
,
![]() .
.
Задача 9.
![]() ,
,
![]()
Задача 10.
![]() ,
,
![]()
Задача 11.
![]() ,
,
![]()
Задача 12.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Задача 13.
![]()
Задача 14.
![]() ,
,
![]()
Задача 15.
1)
![]() ,
,
![]() .
.
2)
![]() ,
,
![]() ,
,
![]() .
.
Задача 17. 600.
Задача 18. 1350.
Задача 19.
![]()
Задача 21.
![]()
Задача 22.
![]()
Задача 23.
![]()
Задача 24.
![]() ,
,
![]() ,
,
![]() .
.
Задача 25.
![]()
Задача 26.
![]()
Задача 27.
![]() ,
,
![]() ,
,
![]()
