АиГ / тема 8
.docКурс “Алгебра и Геометрия”
(спец. прикладная математика, информатика, 1 курс, 1 семестр)
Тема 8. Уравнения плоскости. – 4 ч.
Содержание: общее уравнение плоскости; уравнение плоскости, проходящей через три точки; неполные уравнения плоскости в «отрезках»; нормальное уравнение плоскости, расстояние от точки до плоскости.
Цель: изучить различные способы задания плоскостей в пространстве их уравнениями; научиться применять уравнения плоскостей при решении стереометрических задач.
Форма контроля: опрос.
Задачи
Задача 1 ([8],
915).
Точка
служит основанием перпендикуляра,
опущенного из начала координат на
плоскость. Составить уравнение этой
плоскости.
Задача 2 ([8], 916).
Даны точки
и
составить уравнение плоскости, проходящей
через точку
перпендикулярно вектору
.
Задача 3 ([8], 917).
Составить уравнение плоскости, проходящей
через точку
параллельно векторам
и
.
Задача 4 ([8], 918).
Доказать, что уравнение плоскости,
проходящей через точку
параллельно векторам
и
,
может быть представлено в виде:
.
Задача 5 ([8], 919).
Составить уравнение плоскости, проходящей
через точки
и
параллельно вектору
.
Задача 6 ([8], 920).
Доказать, что уравнение плоскости,
проходящей через точки
и
параллельно вектору
,
может быть представлено в виде:
.
Задача 7 ([8], 921).
Составить уравнение плоскости, проходящей
через точки
,
и
.
Задача 8 ([8], 922).
Доказать, что уравнение плоскости,
проходящей через точки
,
и
,
может быть представлено в виде:
.
Задача 9 ([8], 926).
Определить, при каких значениях
и
следующие
пары уравнений будут определять
параллельные плоскости:
1)
,
;
2)
,
;
3)
,
;
Задача 10 ([8], 928). Определить двугранные углы, образованные пересечением следующих пар плоскостей:
1)
,
2)
3)
,
;
4)
,
.
Задача 11 ([8], 929).
Составить уравнение плоскости, которая
проходит через начало координат
параллельно плоскости
.
Задача 12 ([8], 930).
Составить уравнение плоскости, которая
проходит через точку
параллельно плоскости
.
Задача 13 ([8], 931).
Составить уравнение плоскости, которая
проходит через начало координат
перпендикулярно к двум плоскостям
,
.
Задача 14 ([8], 932).
Составить уравнение плоскости, которая
проходит через точку
перпендикулярно к двум плоскостям
,
.
Задача 15 ([8], 936).
Установить, что три плоскости
,
,
,
имеют одну общую точку, и вычислить её
координаты.
Задача 16 ([8], 937).
Доказать, что три плоскости
,
,
проходят через одну прямую.
Задача 17 ([8], 938).
Доказать, что три плоскости
,
,
пересекаются по трем различным
параллельным прямым.
Задача 18 ([8], 939).
Определить, при каких значениях
и
плоскости
,
,
:
-
Имеют одну общую точку;
-
Проходят через одну прямую;
-
Пересекаются по трем различным параллельным прямым.
Задача 19 ([8],
943]). Найти
точки пересечения плоскости
с координатными осями.
Задача 20 ([8], 946).
Вычислить площадь треугольника, который
отсекает плоскость
от координатного угла Оху.
Задача 21 ([8], 955).
Составить уравнение плоскости,
перпендикулярной к плоскости
и отсекающей на координатных осях Ох и
Оу отрезки
,
.
Задача 22 ([8], 958
[8]). Для каждой
из следующих плоскостей вычислить углы
,
и
,
образуемые нормалью с осями координат,
и расстояние
от начала координат:
1)
;
2)
3)
;
4)
;
5)
6)
;
7)
8)
;
9)
;
10)
Задача 23 ([8], 960).
Вычислить расстояние
от точки
до плоскости, проходящей через точки
,
и
.
Задача 24 ([8], 962).
Доказать, что плоскость
пересекает отрезок, ограниченный точками
и
.
Задача 25 ([8], 963).
Доказать, что плоскость
не пересекает отрезка, ограниченного
точками
и
.
Задача 26 ([8], 965
[8]). Две грани
куба лежат на плоскостях
,
.
Вычислить объем этого куба.
Задача 27 ([8], 966).
На оси Оу найти точку, отстоящую от
плоскости
на расстоянии
.
Задача 28 ([8], 974).
В каждом из следующих случаев определить,
лежат ли точка
и начало координат в одном, в смежных
или вертикальных двугранных углах,
образованных при пересечении двух
плоскостей:
1)
,
;
2)
,
;
3)
,
.
Задача 29 ([8], 975).
В каждом из следующих случаев определить,
лежат ли точки
и
в одном, в смежных или вертикальных
двугранных углах, образованных при
пересечении двух плоскостей:
1)
;
2)
,
.
Задача 30 ([8], 976).
Определить, лежит ли начало координат
внутри острого или тупого угла,
образованного двумя плоскостями
,
.
Задача 31 ([8], 977).
Определить, лежит ли точка
внутри острого или тупого угла,
образованного двумя плоскостями
,
.
Задача 32 ([8], 978).
Составить уравнение плоскости, делящей
пополам тот двугранный угол между двумя
плоскостями
,
,
в котором лежит начало координат.
Задача 33 ([8], 979).
Составить уравнение плоскости, делящей
пополам тот двугранный угол между двумя
плоскостями
,
,
в котором лежит точка
.
Задача 34 ([8], 981).
Составить
уравнение плоскости, которая делит
пополам тупой двугранный угол, образованный
двумя плоскостями
,
.
Тема 8. Плоскость. Различные виды уравнения плоскости.
Ответы
Задача 1.
Задача
2.
Задача
3.
Задача
5.
Задача
7.
Задача 9.
-
,
; -
,
; -
,
.
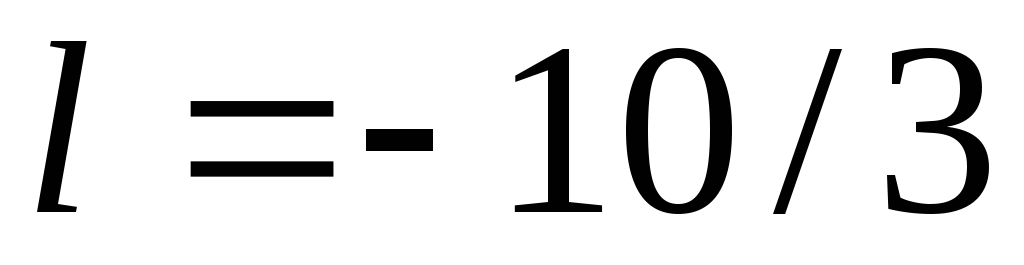Задача 10.
1)
и
;
2)
и
;
3)
;
4)
и
.
Задача
11.
Задача
12.
Задача
13.
Задача
14.
Задача
15.
,
,
.
Задача 18.
1)
;
2)
,
;
3)
,
.
Задача
19.
,
,
.
Задача 20. 240.
Задача
21.
Задача 22.
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
Задача
23.
Задача
26.
.
Задача
27.
Условию задачи удовлетворяют очки
и
.
Задача 28.
1)
Точка
и начало координат лежат в смежных
углах;
2)
Точка
и начало координат лежат в одном углу;
3)
Точка
и начало координат лежат в вертикальных
углах.
Задача 29.
1)
Точки
и
лежат в смежных углах;
2)
Точки
и
лежат в вертикальных углах.
Задача 30. Начало координат лежит внутри острого угла.
Задача 31. Точка лежит внутри тупого угла.
Задача
32.
Задача
33.
Задача
34.
