
Основний змiст дисертацiї
У вступі подається коротка історична довідка з кола питань, що мають відношення до теми роботи. Проведено огляд одержаних результатів, видiленi положення, що виносяться на захист. Нумерація тверджень у дисертації та авторефераті спільна.
У даній роботі при дослідженні коливань гідродинамічних систем систематично застосовуються методи функціонального аналізу, зокрема, методи теорії операторних блок-матриць, метод проектування рівнянь системи на підпростори ортогонального розкладання гільбертова простору, а також методи спектральної теорії операторних жмутків. При вивченні початково-крайових задач істотно використовуються методи теорії диференціальних рівнянь у часткових похідних і диференціально-операторних рівнянь у гільбертовому просторі.
У розділі 1 розглянута постановка задачі про малі рухи ідеальної рідини в басейні, частково вкритому пружним і кришеним льодом. Наведена початково-крайова задача про малі рухи цієї гідромеханічної системи в трьох постановках: у вихідній, що містить поле швидкостей, тиску та вертикальних відхилень рухомої поверхні, у проміжній, що містить потенціал поля швидкостей, і в підсумковій, що містить лише одну шукану функцію — потенціал поля зміщень потенційних рухів рідини. Введена класифікація задачі за трьома рівнями складності. Розділ складається з параграфів 1.1 і 1.2.
Параграф
1.1 присвячений
фізичній і математичній постановці
задачі про малі рухи ідеальної рідини
в басейні
 ,
частково вкритому пружним льодом
(області
,
частково вкритому пружним льодом
(області ),
кришеним
льодом (області
),
кришеним
льодом (області
 ),
а також що має областірухомої
поверхні без
льоду (область
),
а також що має областірухомої
поверхні без
льоду (область
 ).
Межа
).
Межа області
області складається з твердої стінки
складається з твердої стінки ірухомої
поверхні
ірухомої
поверхні
 (
( ).
Вводяться фізичні параметри, які
визначають систему, такі як щільність
).
Вводяться фізичні параметри, які
визначають систему, такі як щільність
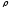 рідини в області
рідини в області ,
поверхнева
щільність пружного льоду
,
поверхнева
щільність пружного льоду
 ікришеного
льоду
ікришеного
льоду ,
а також коефіцієнти жорсткості крижин
,
а також коефіцієнти жорсткості крижин .
Малі рухи рідини описуютьсянаступними
функціями:
.
Малі рухи рідини описуютьсянаступними
функціями:
 — поле малих швидкостей рідини,
— поле малих швидкостей рідини,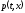 — динамічнийтиск,
— динамічнийтиск,
 — поле вертикальних відхилень рухомої
поверхні від рівноважного
стану.
— поле вертикальних відхилень рухомої
поверхні від рівноважного
стану.
Далі в цьому параграфі виводиться система рівнянь, початкових і граничних умов, яка описує малі рухи рідини, близькі до стану рівноваги. Вона має вигляд:
 (1)
(1)
Тут - оператор потенційної енергії пружноїчастини
системи, за допомогою білінійної
форми якого
- оператор потенційної енергії пружноїчастини
системи, за допомогою білінійної
форми якого
 в зручній формізаписується
закон балансу повної
енергії для класичного розв’язку.
Оператор
в зручній формізаписується
закон балансу повної
енергії для класичного розв’язку.
Оператор
 діє згідно із законом
діє згідно із законом
 (2)
(2)
на (первинній у класичній постановці) області визначення
 .
(3)
.
(3)
Тут
 -
межа
жорсткого
закріплення (межа контакту пружного
льоду з
-
межа
жорсткого
закріплення (межа контакту пружного
льоду з
 ),
),
 ,
(4)
,
(4)
 ,
(5)
,
(5)
де
 — i-а
координата одиничного вектора зовнішньої
нормалі
— i-а
координата одиничного вектора зовнішньої
нормалі
 до межі
до межі
 ,
а
,
а — так звана постійна Пуассона, що
характеризує пружнупластинку,
яка задовольняє нерівностям
— так звана постійна Пуассона, що
характеризує пружнупластинку,
яка задовольняє нерівностям
 .
Дослідження
задачі в роботі
проводиться за принципом "від простого
до складного", в зв'язку з чим в
параграфі
1.1 вводиться
класифікація задачі за трьома рівнями
складності: задачам першого рівня
відповідають випадки, коли рухома
поверхня
.
Дослідження
задачі в роботі
проводиться за принципом "від простого
до складного", в зв'язку з чим в
параграфі
1.1 вводиться
класифікація задачі за трьома рівнями
складності: задачам першого рівня
відповідають випадки, коли рухома
поверхня
 є область лишеодного
типу (три задачі); до задач другого рівня
належать задачі, коли на
є область лишеодного
типу (три задачі); до задач другого рівня
належать задачі, коли на
 стикаються двісереди
(три задачі); до третього рівня віднесена
найбільш загальна
задача, коли на
стикаються двісереди
(три задачі); до третього рівня віднесена
найбільш загальна
задача, коли на
 єділянка
чистої
води, пружного льоду і кришеного
льоду:
єділянка
чистої
води, пружного льоду і кришеного
льоду:
 .
.
У
параграфі 1.2
вводиться
в розгляд простір
 ,
в якому проводиться дослідження задачі,
а також його розкладання вортогональну
суму підпросторів:
,
в якому проводиться дослідження задачі,
а також його розкладання вортогональну
суму підпросторів:
 ,
(6)
,
(6)
 ,
,
 ,
(7)
,
(7)
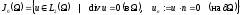 ,
,
 ,
,
 .
.
Далі
в цьому параграфі після
застосування
методу проектування
першого
рівнянь системи (1) на підпростори
ортогонального
розкладання гільбертова
простору
 початкова
задача переформулюється
в проміжну задачу для функцій
початкова
задача переформулюється
в проміжну задачу для функцій
 — потенціалу швидкостей,
— потенціалу швидкостей, — компонента
поля тиску
з
підпростору
— компонента
поля тиску
з
підпростору
 і
і
 :
:
 (8)
(8)
Далі
задача (8) переформульована
в початково-крайову задачу для однієї
шуканої функції — потенціал поля зміщень
частинок рідини з
підпростору
 ,
який визначається таким чином:
,
який визначається таким чином:
 . (9)
. (9)
При цьому початково-крайова задача набуває вигляду:
 (10)
(10)
У кінці параграфа вивчено властивості оператора потенційної енергії пружної частини системи.
Теорема
1.2.3 Оператор
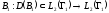 після
його розширення за Фрідріхом — необмежений
самоспряжений
додатно
означений оператор з дискретним спектром,
його спектр складається з скінченнократних
додатних власних
значень
після
його розширення за Фрідріхом — необмежений
самоспряжений
додатно
означений оператор з дискретним спектром,
його спектр складається з скінченнократних
додатних власних
значень
 з граничною точкою
з граничною точкою ,
а власні функції
,
а власні функції утворятьортогональний
базис у
утворятьортогональний
базис у
 :
:

Обернений
оператор
 є компактним і додатним у
є компактним і додатним у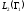 .
Енергетичний простір
.
Енергетичний простір оператора
оператора складається з тих елементівз
складається з тих елементівз
 ,
для яких кінцева квадратична форма
,
для яких кінцева квадратична форма
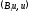 ,
причому
,
причому .
.
У розділі 2 розглянуто три задачі першого рівня з наведеної класифікації. Вивчено відповідні початково-крайові задачі, для всіх задач доведено теореми про сильну розв’язність. Досліджено також відповідні спектральні задачі. Розділ складається з параграфів 2.1–2.3.
Параграф 2.1 присвячений вивченню задачі про малі коливання ідеальної рідини в басейні з вільною поверхнею, тобто коли на рухомій поверхні немає ні пружного, ні кришеного льоду. Задача є класичною і досліджувалася раніше багатьма авторами. Однак нарівні з відомими фактами в даному параграфі отримано нові результати, пов'язані з умовами сильної розв’язності початково-крайової задачі.
С
цією ціллю вихідна початково-крайова
задача (10) для потенціалу зміщень
 ,
який є розв’язком задачі Неймана
,
який є розв’язком задачі Неймана
 (11)
(11)
(тут
 — функція відхиленьрухомої
поверхні від її рівноважного
положення),
зведена в гільбертовому
просторі
— функція відхиленьрухомої
поверхні від її рівноважного
положення),
зведена в гільбертовому
просторі до еквівалентної задачі Кошінаступного
вигляду:
до еквівалентної задачі Кошінаступного
вигляду:
 (12)
(12)
де
оператор
 є лінійним компактнимсамоспряженим
додатним
оператором, що діє
в просторі
є лінійним компактнимсамоспряженим
додатним
оператором, що діє
в просторі
 .
.
Далі
в цьому параграфі досліджена абстрактна
задача Коші для лінійного диференціального
рівняння другого порядку в довільному
гільбертовому
просторі
 наступного
вигляду:
наступного
вигляду:
 (13)
(13)
 (14)
(14)
Тут
 — простір лінійних обмежених операторів,
щодіють
у
просторі
— простір лінійних обмежених операторів,
щодіють
у
просторі
 .
.
Означення
2.1.1. Будемо
говорити, що функція
 ,
,
 ,
є сильним розв’язком
задачі
Коші (13) зі
значеннями в
,
є сильним розв’язком
задачі
Коші (13) зі
значеннями в
 ,
якщо
виконані наступні
умови:
,
якщо
виконані наступні
умови:
 і
і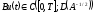 ,
функція
,
функція двічі неперервно диференційовна,
двічі неперервно диференційовна, і виконано рівняння (13)при
будь-якому
і виконано рівняння (13)при
будь-якому
 .
.
Теорема 2.1.6. Якщо виконані умови
![]() (15)
(15)
то
задача Коші (13) має єдиний сильний
розв’язок
(зі значеннями в
 )
на відрізку
)
на відрізку .
.
Нарівні із задачею (13) виявляється також корисною задача вигляду
 (16)
(16)
з
тими ж умовами (14) на операторні
коефіцієнти. Осібно вивчені окремі
випадки задач (13) і (16), коли
 і
і .
Для нихотримано
відповідні умови сильної розв’язності.
Далі введене поняття узагальненого
розв’язку
задачі Коші (13) з неперервною повною
енергією і отримано
умови його існування.
.
Для нихотримано
відповідні умови сильної розв’язності.
Далі введене поняття узагальненого
розв’язку
задачі Коші (13) з неперервною повною
енергією і отримано
умови його існування.
Вибір абстрактної задачі у вигляді (13)–(14) визначається тим, що всі задачі трьох рівнів складності, розглянуті в даній роботі, зводяться до задачі такого вигляду. Відмінність в задачах складається у властивостях операторних коефіцієнтів, що приводить до різних умов розв’язності еволюційних задач. Однак схема дослідження зберігається і результати для абстрактних задач Коші (13) і (16) істотно використовуються надалі.
Означення
2.1.5. Сильним
(за змінною
 )
розв’язком
задачі
(1) (для випадку поверхні рідини без
льоду) на проміжку
)
розв’язком
задачі
(1) (для випадку поверхні рідини без
льоду) на проміжку
 назвемо
набір функцій
назвемо
набір функцій
 ,
,
 і
і
 ,
для яких виконанінаступні
умови: 1.
,
для яких виконанінаступні
умови: 1.
 ,
, і
при
будь-якому
і
при
будь-якому
 справедливе перше рівняння (1); 2.
справедливе перше рівняння (1); 2.
 ,
, ;
3.
виконана гранична умова на
;
3.
виконана гранична умова на
 :
:
 ;
4.
виконані початкові умови (1).
;
4.
виконані початкові умови (1).
Тут
 .
Аналогічно вводяться означення сильних
(за змінною
.
Аналогічно вводяться означення сильних
(за змінною )
розв’язків задач (10) і (8).
)
розв’язків задач (10) і (8).
Теорема
2.1.16. Якщо
виконані умови
 ,
,
 ,
, ,
, ,
,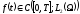 ,
то кожна із
задач (10), (8) і (1) (випадок поверхні рідини
без льоду) має єдиний сильний за
,
то кожна із
задач (10), (8) і (1) (випадок поверхні рідини
без льоду) має єдиний сильний за
 розв’язок
в значенні
означення 2.1.5.
розв’язок
в значенні
означення 2.1.5.
Для початково-крайової задачі (1) доведена також теорема про існування узагальненого розв’язку з неперервною повною енергією. Наведено прості достатні умови сильної розв’язності, в яких вказується гладкість початкового поля швидкостей і функції відхилень рухомої поверхні від її рівноважного стану, а також поля зовнішніх впливів.
Зауваження
2.1.17. Якщо
виконані умови
 ,
,
 ,
, ,
, ,
, ,
то задача (1) (випадок поверхні рідини
без льоду) має єдиний сильний за
,
то задача (1) (випадок поверхні рідини
без льоду) має єдиний сильний за
 розв’язок.
розв’язок.
Далі
розглянуто так звані нормальні коливання,
тобто розв’язки
задачі (12) ( ),
що залежать від часу згідно із законом
),
що залежать від часу згідно із законом (
( — частота власних коливань). Як відомо,
відповідна спектральна задача Стеклова
— частота власних коливань). Як відомо,
відповідна спектральна задача Стеклова
 (17)
(17)
має
дискретний додатний спектр
 ,
,
 ,
з асимптотичною
поведінкою
,
з асимптотичною
поведінкою
 ,
(18)
,
(18)
при
цьому система власних елементів
 ,
що відповідає власним значенням
,
що відповідає власним значенням ,
утворюєортонормований
базис у
,
утворюєортонормований
базис у
 .
.
У параграфі 2.2 розглянуто задачу про малі коливання ідеальної рідини, вкритої пружним льодом. Пружний лід моделюється пружною пластинкою. Близька задача розглядалася раніше, наприклад, в монографії М.Д. Копачевського, С.Г. Крейна, Нго Зуй Кана. У даному параграфі нарівні з відомими фактами отримано умови сильної розв’язності початково-крайової задачі (1) в цьому випадку.
Тут задача (10) зведена до еквівалентної задачі Коші наступного вигляду:
 (19)
(19)
Для
оператора
 встановлено
(лема 2.1.1), що він є додатно означеним
необмеженим оператором у
встановлено
(лема 2.1.1), що він є додатно означеним
необмеженим оператором у
 з
компактним додатним оберненим. Оператор
з
компактним додатним оберненим. Оператор ,
як і в попередній задачі, є додатним і
компактним.
,
як і в попередній задачі, є додатним і
компактним.
Відповідна спектральна задача
 (20)
(20)
має
дискретний додатний спектр з граничною
точкою
 і засимптотичною
поведінкою
і засимптотичною
поведінкою
 ,
(21)
,
(21)
а
система власних елементів утворює
ортогональний базис в
 .
Формула (21) немістить
інформації, пов'язаної з наявністю
рідини в контейнері, тобто великі за
номером
.
Формула (21) немістить
інформації, пов'язаної з наявністю
рідини в контейнері, тобто великі за
номером
 моди коливань рідини визначаються
головним чином коливаннями пружноїрухомої
поверхні.
моди коливань рідини визначаються
головним чином коливаннями пружноїрухомої
поверхні.
Теорема
2.2.5. Якщо
виконані умови
 ,
,
 ,
, ,
, ,
, ,
, ,
,
 ,то
кожна із
задач (10), (8) і (1) (випадок пружного льоду)
має єдиний сильний за
,то
кожна із
задач (10), (8) і (1) (випадок пружного льоду)
має єдиний сильний за
 розв’язок.
розв’язок.
Зауваження
2.2.6. З
вигляду
оператора
 (див. (2)) і його області визначення до
розширення (див. (3)) можназаписати
більш прості достатні умови сильної
розв’язності:
(див. (2)) і його області визначення до
розширення (див. (3)) можназаписати
більш прості достатні умови сильної
розв’язності:
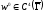 ,
,
 ,
, ,
, ,
, ,
, ,
, ,
, .
Для поля зовнішніх сил достатньо
поставити вимогу
.
Для поля зовнішніх сил достатньо
поставити вимогу
 .
.
Для початково-крайової задачі (1) в цьому випадку доведена теорема про існування узагальненого розв’язку з неперервною повною енергією.
Параграф 2.3 присвячений розгляду третьої задачі першого рівня, коли рухома поверхня повністю вкрита кришеним льодом. Під кришеним льодом тут розуміються вагомі частинки деякої речовини, які в процесі коливань поверхні один з одним не взаємодіють або їх взаємодія зневажливо мала. Перші дослідження задач подібного виду, пов'язані з вивченням явища флотації, проведені С.О. Габовим і О.Г. Свешниковим.
У даній роботі початкова задача зведена до рівносильної задачі Коші в гільбертовому просторі:
 (22)
(22)
Тут
оператор
 той, що і в (12) та (20).
той, що і в (12) та (20).
Теорема
2.3.2. Нехай
виконані умови
 ,
,
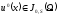 ,
, ,
, .
Тоді кожна із
задач (10), (8) і (1) (випадок кришеного
льоду) має єдиний сильний за
.
Тоді кожна із
задач (10), (8) і (1) (випадок кришеного
льоду) має єдиний сильний за
 розв’язок.
розв’язок.
Ця теорема посилює відповідну теорему про розв’язність з роботи С.О. Габова і О.Г. Свешникова.
Відповідна спектральна задача має вигляд:
 (23)
(23)
Доведено,
що вона має дискретний додатний спектр
з граничною точкою
 ,
а система власних елементів утворює
ортогональний базис в
,
а система власних елементів утворює
ортогональний базис в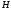 .
Показано, що наявністькришеного
льоду на поверхні рідини породжує новий
тип хвиль з частотами, близькими до
частоти вільних коливань часток кришеного
льоду на поверхні. Для цих хвиль
встановлена
асимптотична
поведінка власних значень
.
Показано, що наявністькришеного
льоду на поверхні рідини породжує новий
тип хвиль з частотами, близькими до
частоти вільних коливань часток кришеного
льоду на поверхні. Для цих хвиль
встановлена
асимптотична
поведінка власних значень
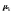 має вигляд
має вигляд
 .
(24)
.
(24)
У
розділі
3 розглянуто
три задачі другого рівня складності.
Тут для отримання операторного
диференційного рівняння виду (13)
використано метод проектування граничних
умов на підпростори
спеціальним чином
побудованого
ортогонального
розкладання гільбертова
простору
 .
Досліджені початково-крайові та
спектральні задачі.Отримані
достатні умови сильної розв’язності
вихідної початково-крайової задачі.
Розділ
складається з параграфів 3.1–3.3.
.
Досліджені початково-крайові та
спектральні задачі.Отримані
достатні умови сильної розв’язності
вихідної початково-крайової задачі.
Розділ
складається з параграфів 3.1–3.3.
У
параграфі 3.1 розглянутий
випадок, коли рідина вкрита кришеним
льодом
і є ділянки
чистої
води. Перші дослідження цієї задачі у
проблемі флотації здійснені С.О. Габовим
і О.Г. Свєшниковим. В цієї роботі для
отримання операторного диференційного
рівняння виду (13) застосований новий
підхід — граничні умови на рухомій
поверхні проектуються на підпростори
ортогонального
розкладання
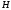 :
:
 ,
,
 ,
(25)
,
(25)
 , (26)
, (26)
 , (27)
, (27)
де
функція
 відхилення рухомої поверхні від їїрівноважного
стану
представлена
у вигляді пари функцій:
відхилення рухомої поверхні від їїрівноважного
стану
представлена
у вигляді пари функцій:
 ,
,
 и
и
 .
(Зазначимо, щоортогональне
розкладання (25) природним чином
пристосоване до застосування
методу ортогонального
проектування для вихідної задачі, тобто
для випадку, коли на різних ділянках
рухомої
межі задані різні граничні умови.)
.
(Зазначимо, щоортогональне
розкладання (25) природним чином
пристосоване до застосування
методу ортогонального
проектування для вихідної задачі, тобто
для випадку, коли на різних ділянках
рухомої
межі задані різні граничні умови.)
Операторне рівняння задачі тут має вигляд
 (28)
(28)
де
 ,
,
 — це операторні
блок-матриці. Для виводу рівняння (28)
розглядаються
три допоміжні задачі для потенціалу
зміщення, пов'язані з проектуванням
граничних умов на поверхні
— це операторні
блок-матриці. Для виводу рівняння (28)
розглядаються
три допоміжні задачі для потенціалу
зміщення, пов'язані з проектуванням
граничних умов на поверхні
 .
.
Доведено,
що
 — самоспряжена компактна і додатнаоператорна
матриця,
що діє
в
просторі
— самоспряжена компактна і додатнаоператорна
матриця,
що діє
в
просторі
 .
Оператор
.
Оператор — самоспряжений обмежений і невід’ємний
(з нескінченновимірним ядром).
— самоспряжений обмежений і невід’ємний
(з нескінченновимірним ядром).
З застосуванням методу операторних блок-матриць, а також загальної схеми розгляду еволюційних задач, яка викладена в параграфі 2.1, доведено теореми про сильну розв’язність задачі (28) (теорема 3.1.5) і вихідної початково-крайової задачі:
Теорема
3.1.8. Якщо
виконані умови
 ,
,
 ,
, ,
, ,
, ,
, ,
, ,
, ,
тоді кожна із
задач (10), (8) і (1) (випадок кришеного
льоду з ділянками чистої води) має єдиний
сильний за
,
тоді кожна із
задач (10), (8) і (1) (випадок кришеного
льоду з ділянками чистої води) має єдиний
сильний за
 розв’язок.
розв’язок.
Для відповідної спектральної задачі
 (29)
(29)
встановлено наступні факти.
Теорема
3.1.10. Задача
(29) має дискретний додатний спектр з
граничними точками на нескінченності
і в точці
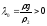 .
Гілки власних значень
.
Гілки власних значень з граничною точкою на
з граничною точкою на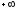 відповідають хвилі, характерні для
рідини в басейніз
вільною
поверхнею і з асимптотичною
поведінкою
відповідають хвилі, характерні для
рідини в басейніз
вільною
поверхнею і з асимптотичною
поведінкою
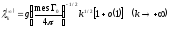 .
(30)
.
(30)
Гілці
власних значень
 з граничною точкою
з граничною точкою відповідає інший тип хвиль,зумовлених
наявністю кришеного
льоду на поверхні. Ці власні значення
мають асимптотичну
поведінку
відповідає інший тип хвиль,зумовлених
наявністю кришеного
льоду на поверхні. Ці власні значення
мають асимптотичну
поведінку
 .
(31)
.
(31)
Сукупність
всіх власних елементів утворює
ортогональний
базис в просторі
 .
.
Наявність рухомих поверхонь двох типів, а саме області з кришеного льоду і області поверхні рідини без льоду, приводить до появи двох гілок частот власних коливань з поведінкою, характерною для кожної з поверхонь окремо.
У параграфі 3.2 розглянута задача, коли рідина повністю вкрита пружним і кришеним льодом. Для отримання операторного рівняння цієї задачі, як і раніше, використовується метод ортогонального проектування граничних умов на рухомій поверхні на підпростори ортогонального розкладання
 ,
(32)
,
(32)
 , (33)
, (33)
 , (34)
, (34)
а
для підпростору доведено,
що воно є одномірним.
доведено,
що воно є одномірним.
Операторне рівняння задачі в цьому випадку має вигляд
 (35)
(35)
Тут
 ,
,
 ,
, — це операторні
блок-матриці. Досліджено властивості
цих операторів. Доведено, що
— це операторні
блок-матриці. Досліджено властивості
цих операторів. Доведено, що
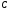 — самоспряжена компактна і додатнаоператорна
матриця, що діє
в просторі
— самоспряжена компактна і додатнаоператорна
матриця, що діє
в просторі
 .
Оператор
.
Оператор є необмеженим самоспряженим додатно
означеним оператором з обмеженим
додатним оберненим. Оператор
є необмеженим самоспряженим додатно
означеним оператором з обмеженим
додатним оберненим. Оператор є обмеженим додатно означеним оператором.
є обмеженим додатно означеним оператором.
Для
виводу (35) розглядаються
дві допоміжні задачі для потенціалу
зміщення, пов'язані з проектуванням
граничних умов на поверхні
 .
.
Далі в параграфі досліджена відповідна спектральна задача
 (36)
(36)
На
основі властивостей операторів задачі
показано, що задача (36) має дискретний
додатний спектр, який складається з
двох гілок власних значень з граничними
точками на нескінченності і в точці
 .
Доведенабазисность
сукупності всіх власних елементів
задачі (36) в просторі
.
Доведенабазисность
сукупності всіх власних елементів
задачі (36) в просторі
 .
.
Отримано також достатні умови сильної розв’язності задачі (35) (теорема 3.2.8) і вихідної початково-крайової задачі про малі рухи рідини в басейні, повністю вкритому пружним і кришеним льодом (теорема 3.2.9).
У параграфі 3.3 розглянута остання із задач другого рівня складності, коли рідина частково вкрита пружним льодом і є області поверхні рідини без льоду. Близька задача про коливання рідини в частково заповненому контейнері з пружним днищем розглядалася М.Д. Копачевським, С.Г. Крейном, Нго Зуй Каном в їх монографії. Однак питання про сильну розв’язність еволюційної задачі там не розглядалося.
З використанням методу ортогонального проектування граничних умов на рухомій поверхні і введенням двох допоміжних задач для потенціалу зміщень вихідна початково-крайова задача зводиться до рівносильної задачі Коші
 (37)
(37)
Доведено
наступні
леми
про властивості операторних
блок-матриць:
 — самоспряжена компактна і додатнаоператорна
матриця, що діє
в просторі
— самоспряжена компактна і додатнаоператорна
матриця, що діє
в просторі
 ;
оператор
;
оператор є необмеженим самоспряженим додатно
означеним оператором з обмеженим
додатним оберненим; оператор
є необмеженим самоспряженим додатно
означеним оператором з обмеженим
додатним оберненим; оператор є обмеженим і невід’ємним
оператором (з нескінченновимірним
ядром).
є обмеженим і невід’ємним
оператором (з нескінченновимірним
ядром).
Далі доведено, що відповідна спектральна задача
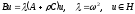 (38)
(38)
має
дискретний додатний спектр з граничною
точкою на нескінченності. Доведена
також ортогональна базисность
сукупності всіх власних елементів
задачі в просторі
 .
.
Із застосуванням загальної схеми розгляду еволюційних задач, яка викладена в параграфі 2.1, доведено теореми про сильну розв’язність задачі (37) (теорема 3.3.8) і вихідної початково-крайової задачі (теорема 3.3.10).
У розділі 4 розглядається найбільш загальний випадок, коли на поверхні рідини є області кришеного і пружного льоду, а також ділянки поверхні рідини без льоду. Вивчено також випадок, коли на рухомій поверхні є ділянки кришеного льоду різної постійної щільності. Для кожного випадку досліджено відповідні еволюційні і спектральні задачі. Розділ складається з параграфів 4.1–4.2.
У
параграфі 4.1 розглянута
задача, коли рухома поверхня складається
з трьох областей: поверхні рідини без
льоду
 ,
ділянки
пружного
льоду
,
ділянки
пружного
льоду
 іділянки
кришеного
льоду
іділянки
кришеного
льоду
 .
Длязастосування
методу ортогонального
проектування граничних умов на рухомій
поверхні в цьому випадку використовується
розкладання
.
Длязастосування
методу ортогонального
проектування граничних умов на рухомій
поверхні в цьому випадку використовується
розкладання
 на трипідпростори:
на трипідпростори:
 (39)
(39)
Тут
 , (40)
, (40)
 , (41)
, (41)
 , (42)
, (42)
де
функція
 відхилення рухомої поверхні від їїрівноважного
стану
зображена у
вигляді трійки функцій
відхилення рухомої поверхні від їїрівноважного
стану
зображена у
вигляді трійки функцій
 ,
,
 ,
, Доведено, що
Доведено, що
 єдвомірний
підпростір (лема
4.1.1).
єдвомірний
підпростір (лема
4.1.1).
Після
проектування граничних умов на підпростори
 ,
,
 і
і
 ,
вихідна початково-крайова задача була
зведена вгільбертовому
просторі
,
вихідна початково-крайова задача була
зведена вгільбертовому
просторі
 до еквівалентної задачі Кошінаступного
вигляду:
до еквівалентної задачі Кошінаступного
вигляду:
 (43)
(43)
Для
виводу (43) розглядаються
три допоміжні задачі для потенціалу
зміщення, пов'язані з проектуванням
граничних умов на поверхні
 напідпростори
напідпростори
 .
Для операторних
коефіцієнтів доведено наступні
властивості:
.
Для операторних
коефіцієнтів доведено наступні
властивості:
 — самоспряжена компактна і додатнаоператорна
матриця, що діє
в просторі
— самоспряжена компактна і додатнаоператорна
матриця, що діє
в просторі
 ;
оператор
;
оператор є обмежений невід’ємний
оператор (з нескінченновимірним
ядром); оператор
є обмежений невід’ємний
оператор (з нескінченновимірним
ядром); оператор
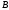 є необмеженим самоспряженим додатно
означеним оператором з обмеженим
додатним оберненим.
є необмеженим самоспряженим додатно
означеним оператором з обмеженим
додатним оберненим.
Далі досліджена відповідна спектральна задача
 (44)
(44)
Теорема
4.1.9. Задача
(44) має дискретний додатний спектр з
двома граничними точками на нескінченності
і в точці
 .
Сукупність всіх власних елементів
задачі утворюєортогональний
базис в просторі
.
Сукупність всіх власних елементів
задачі утворюєортогональний
базис в просторі
 і за формою оператору
і за формою оператору :
:
 ,
,
 .
.
Означення
4.1.3. Сильним
(за змінною
 )
розв’язком
задачі (1) на проміжку
)
розв’язком
задачі (1) на проміжку
 назвемо
набір функцій
назвемо
набір функцій
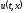 ,
,
 і
і
 ,
для яких виконанінаступні
умови: 1.
,
для яких виконанінаступні
умови: 1.
 ,
, ,
і при
будь-якому
,
і при
будь-якому
 справедливе перше рівняння (1); 2.
справедливе перше рівняння (1); 2.
 ;
3.
виконані граничні умови на
;
3.
виконані граничні умови на
 ,
,
 і
і
 :
:
 ,
, ,
,
 ,
де всі доданки є неперервними за
,
де всі доданки є неперервними за
 функціямизі
значеннями в
функціямизі
значеннями в
 ,
,
 і
і
 ;
4.
виконані початкові умови (1).
;
4.
виконані початкові умови (1).
Теорема
4.1.12. Якщо
виконані умови
 ,
,
 ,
, ,
, ,
,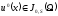 ,
, ,
, ,
, ,
, ,
, ,
то кожна із
задач (10), (8) і (1) має єдиний сильний за
,
то кожна із
задач (10), (8) і (1) має єдиний сильний за
 розв’язок
в значенні
означення 4.1.3.
розв’язок
в значенні
означення 4.1.3.
У
параграфі 4.2 вивчено
одне
з
узагальнень задачі параграфа 3.1, а саме,
досліджено випадок, коли на рухомій
поверхні рідини є декілька
(а саме
 )
областейкришеного
льоду різної постійної щільності.
)
областейкришеного
льоду різної постійної щільності.
Для
цієї задачі отримано
систему рівнянь, граничних і початкових
умов для потенціалу зміщень
 ,
яка описує малі рухи рідини в басейні.
,
яка описує малі рухи рідини в басейні.
Для
отримання операторного
рівняння задачі розглядається
ортогональне
розкладання простору
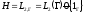 на
на підпростори:
підпростори:
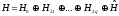 .
(45)
.
(45)
Тут
підпростори визначаються таким чином.
Функцію
 відхилення рухомої поверхні від їїрівноважного
стану
розглядаємо
у вигляді набору функцій, заданих на
відповідних областях
відхилення рухомої поверхні від їїрівноважного
стану
розглядаємо
у вигляді набору функцій, заданих на
відповідних областях
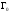 і
і ,
,
 ,
де
,
де
 ,
,
 ,
,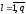 ;
при цьому
;
при цьому
 ,
,
 .
.
Для
підпростору
 доведено (лема 4.2.1), що воно є
доведено (лема 4.2.1), що воно є
 -мірним
підпростором
простору
-мірним
підпростором
простору
 .
.
Операторне рівняння задачі тут має вигляд
 (46)
(46)
Оператор
 — самоспряжений компактний і додатний
оператор, щодіє
в просторі
— самоспряжений компактний і додатний
оператор, щодіє
в просторі
 .
Оператор
.
Оператор — самоспряжений обмежений і невід’ємний.
— самоспряжений обмежений і невід’ємний.
Спектральна задача, відповідна задачі Коші (46), має наступний вигляд:
 (47)
(47)
Теорема
4.2.6. Задача
(47) має дискретний додатний спектр, що
складається з
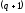 гілок власних значень з граничними
точками на нескінченності і в точках
гілок власних значень з граничними
точками на нескінченності і в точках
 ,
,
 .
Сукупність всіх власних елементів
оператора
.
Сукупність всіх власних елементів
оператора
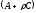 утворюєортогональний
базис в просторі
утворюєортогональний
базис в просторі
 .
.
Наявність на поверхні рідини областей кришеного льоду різної щільності приводить до наявності нового типу хвиль з частотами, близькими до частот вільних коливань частинок кришеного льоду для кожної з областей.
