Chast_4_1_l_22-24

262

Формула (4.35) указывает на то, что, если 2 1 и 2 конечно, то

1 0 , т.е. в этом случае силовые линии В подходят к ферромагнетику с магнитной проницаемостью 2 под прямым углом. Напряженность магнитного поля Н2 в этом случае

H2 B2 0

2

Эта ситуация будет наблюдаться тогда, когда при очень больших 2

( 2 ) геометрия магнитной системы такова, что в магнетике с магнитной проницаемостью 2 нельзя образовать замкнутый контур, охватывающий ток. Тогда В2 конечно и B1 0, а H2 0 . Приведем примеры.

На рис. 4.30 внутри магнетика с 2 нельзя образовать замкнутый контур, охватывающий ток.

На рис. 4.31 внутри магнетика с 2 можно образовать замкнутый контур, охватывающий ток.

Рис. 4.30. Силовые линии подходят к магнетику с 2 под прямым углом

Рис. 4.31. Силовые линии подходят к магнетику с 2 не под прямым углом

Силовые линии поля В касательны к проводнику, находящемуся в высокочастотном электромагнитном поле, так как В2п 0, и в соответствии с универсальным граничным условием (4.33) В1п 0 (рис. 4.32).

263

Рис. 4.32. Магнитное поле обтекает проводник в случае высокочастотного электромагнитного поля

Рассмотрим, наконец, граничное условие для плотности тока (рис.

4.33).

Рис. 4.33. К выводу граничного условия для плотности тока

Применяя закон сохранения заряда в интегральной форме к замкнутой поверхности S , ограничивающей диск, находим

Если для указанной замкнутой поверхности диска S применить принцип непрерывности электрического тока

то получим граничное условие в таком виде:

Вопросы и задачи к лекции 24

266-1. Запишите систему уравнений Максвелла в дифференциальной форме для электромагнитного поля в среде. Поясните смысл всех векторов поля, входящих в эти уравнения.

267-2. Запишите систему уравнений Максвелла в интегральной форме для электромагнитного поля в среде.

268-3. Выведите граничные условия для векторов электрического поля

D и на границе раздела двух сред. Какое условие является универсальным, а какое нет? Почему?

269-4. Чем обусловлен скачок нормальной компоненты на границе двух диэлектриков?

270-5. Выведите граничные условия для векторов магнитного поля В и

на границе раздела двух сред. Какое условие является универсальным, а

какое нет? Почему?

271-6. Чем обусловлен скачок тангенциальных компонент В на границе двух магнетиков?

272-7. Сформулируйте граничные условия на границе проводника в случае электростатического поля и в случае высокочастотного электромагнитного поля.

273-8. Зарисуйте примерную картину силовых линий вектора В (рис.

4.34)

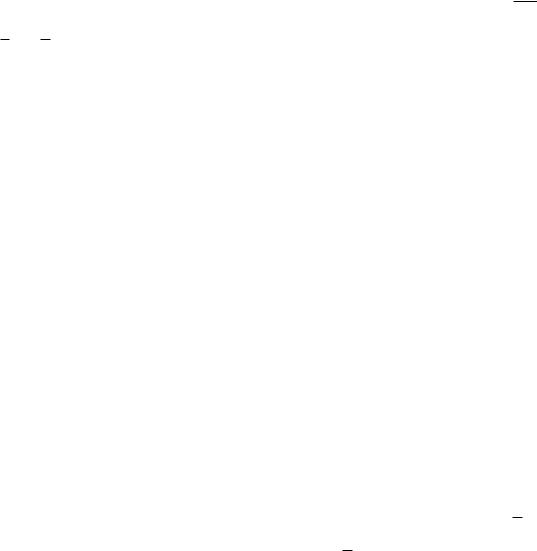
265

Рис. 4.34. Проводник с током и магнитопровод, имеющий зазор

274-9. Проводник находится в электростатическом поле. Среда,

окружающая проводник — воздух. В некоторой точке на поверхности

проводника поверхностная плотность свободного заряда 0,001 Кл .

м2

Найдите D и в этой точке.

275-10. Сформулируйте граничные условия для плотности тока.

Лекция 25 57. Энергия и поток энергии электромагнитного поля в

Умножим скалярно левую и правую части первого уравнения на E , а

левую и правую части второго уравнения - на H и вычтем из второго уравнения первое. Получим

Предположим, что и не зависят от времени. Тогда: