Chast_4_1_l_22-24

233

qi ri – дипольный или электрический момент зарядов, расположенных в

i

физически бесконечно малом объеме V ; pi – дипольный момент i-ой молекулы. Заряды диэлектрика будем считать неподвижными.

Под напряженностью электрического поля внутри диэлектрика будем понимать усредненное значение истинной напряженности по физически

В дальнейшем нам придется находить уравнения для макроскопических (усредненных) величин, исходя из уравнений для микроскопических величин. При этом нам придется пользоваться следующими равенствами

Второе равенство сразу следует из (4.2). Докажем первое:

Среднее значение в точках М и М´ равно:

Здесь V и V - два одинаковых шара, центры которых смещены вдоль х на величину x (рис. 4.2).

Рис. 4.2. К выводу равенства для производных по координате

235

Мы обозначим E E , своб , а связ выразим через P .

Выделим в диэлектрике объем V, ограниченный замкнутой поверхностью S (рис. 4.3).

Рис. 4.3. Диэлектрик в поле точечного заряда

Поверхность S пересечет некоторое число молекул так, что одни из зарядов этих молекул окажутся вне объема V, а другие внутри него. Поэтому в V

может оказаться суммарный связанный заряд. Найдем его.

Рис. 4.4. «Перерезание» диполей элементарной площадкой S

Элемент S пересечет все те диполи, центры которых расположены в прилегающем к нему слое толщины l cos l n (рис. 4.4)

P p N p N ql .

Здесь N – число диполей в единице объема. Следовательно, число диполей,

рассекаемых элементом S

N S l cos l n

Нескомпенсированный заряд, в объеме V за счет этого пересечения:

q N ql S cos l n P S cos P n Pn S .

Следовательно:

q Pn S P S .

236

Суммарный связанный заряд, попавший внутрь замкнутой

поверхности:

Здесь использована математическая теорема Гаусса-Остроградского.

С другой стороны:

т.е.:

qсвяз связdV .

V

Отсюда связ divP . Поэтому:

div E divP ,

0 0 div 0E P .

По определению сумма 0E P называется вектором электрического смещения и обозначается через D .

– постулат Максвелла в дифференциальной форме.

SV

–постулат Максвелла в интегральной форме.

Очевидно, чем больше напряженность электрического поля в диэлектрике, тем больше он поляризуется, т.е. тем больше вектор поляризации P :

238

Образуем мысленно около точки М физически бесконечно малый дискообразный объем V S l , причем точка М лежит в центре этого

где E создается всеми свободными и всеми связанными зарядами, за исключением связанных зарядов объема V . Тогда E создается связанными зарядами объема V .

Выразим E через P . Для этого изобразим объем V в увеличенном виде (рис. 4.6 слева).

Заряды диполей внутри объема V компенсируют друг друга. Поэтому для расчета поля зарядов объема V можно использовать следующую модель (рис. 4.6 справа).

Рис. 4.6. Поляризованный элементарный объем V в окрестности точки наблюдения М

На правом основании - положительные заряды с поверхностной плотностью

связ , а на левом основании - отрицательные заряды с поверхностной плотностью ( связ ). Других зарядов нет.

Легко находим (так как l 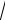S ):

240

246-1. Опишите процесс поляризации диэлектрика.

247-2. Дайте определение вектора поляризации.

248-3. Докажите равенства и .

x x t t

249-4. Выведите постулат Максвелла в дифференциальной форме.

250-5. Выведите постулат Максвелла в интегральной форме.

251-6.Запишите материальное уравнение для электрического поля в диэлектрике.

252-7.Электрическое поле создается точеным зарядом (рис. 4.7).

Рис. 4.7. Диэлектрический шар в поле точечного заряда

Укажите направление вектора поляризации в точке М (центре диэлектрического шара). Когда будет больше напряженность электрического поля в точке М: при наличии диэлектрического шара или при его отсутствии?

Какой величине будет равна напряженность электрического поля в точке М,

если шар будет проводящим?

253-8.Какой физический смысл вектора электрического смещения D в

диэлектрике? Поясните ответ.

254-9. Задано напряжение между обкладками двухслойного плоского конденсатора U (рис. 4.8). Толщины слоев d1 и d2 , диэлектрические проницаемости соответственно и 0 . Сумма d1 + d2 значительно меньше поперечных размеров конденсатора. Найдите вектор электрического смещения в первом и втором слое D1 и D2 , а также напряженность электрического поля в первом и во втором слое Е1 и Е2 .

241

Рис. 4.8. Двухслойный плоский конденсатор

255-10. Бесконечно длинная прямолинейная нить с зарядом на единицу длины располагается в диэлектрике с проницаемостью (рис.4.9).

Диэлектрик представляет собой бесконечно длинный круговой цилиндр радиуса R. Нить является осью этого цилиндра. Найдите выражение для Е и

D в диэлектрике и в воздухе. Найдите поверхностную плотность связанного заряда связ на боковой поверхности цилиндра.

Рис. 4.9. Бесконечная нить, окруженная слоем диэлектрика

Лекция 23 53. Векторы намагниченности и напряженности магнитного поля.

Закон полного тока в среде

В любой среде существуют микротоки: движение электронов по орбитам, спиновое движение электронов. При внесении вещества в магнитное поле магнитные моменты микротоков приобретают определенную ориентацию (до внесения в магнитное поле они имели хаотическую ориентацию и магнитное поле не создавали), как правило, по магнитному полю. Говорят, что вещество намагничивается. Степень намагниченности вещества в данной точке характеризуют вектором намагниченности. Вектор намагниченности J – это магнитный момент единицы объема вещества