Дифференциальные уравнения первого порядка с разделяющимися переменными

Определение: Уравнение вида

называется уравнением с разделяющимися переменными.

Решение: .

Разделив обе части на , получим:

.

Проинтегрировав, обе части уравнения, получим:

.

Пример. Найти общий интеграл уравнения: .

Решение: ,

,

Разделим обе части уравнения на , получим:

,

проинтегрируем обе части

,

Ответ: .

Однородные дифференциальные уравнения

К уравнению с разделяющимися переменными приводятся однородные дифференциальные уравнения первого порядка.

Определение: Функция называется однородной функцией n-го порядка, если при умножении каждого аргумента на произвольный множитель вся функция умножится на, т е.

Например, функция есть однородная функция четвертого порядка, поскольку

Определение: Дифференциальное уравнение

называется однородным, если функция есть однородная функция нулевого порядка.

Это уравнение приводится к виду , и решается подстановкой или и.

Однородное уравнение часто задается в дифференциальной форме

,

где и- однородные функции одинакового порядка.

Пример. Найти общий интеграл уравнения

.

Решение: Данное уравнение однородное, т. к. функции и- однородные функции второго порядка.

Положим ,тогда . Подставляем в исходное уравнение:

,

,

,

.

Разделим, и левую, и правую стороны на , получаем:

,

отсюда, интегрируя, находим

,

,

.

Подставляя , получим общий интеграл исходного уравнения:

,

Ответ: .

Линейные дифференциальные уравнения первого порядка

Определение: Дифференциальное уравнение первого порядка называется линейным, если его можно записать в виде:

, (3).

где и- заданные функции или постоянные.

Будем искать решение в виде произведения двух функций, зависящих от х, т.е.

,

где одна из функций произвольная, другую мы определяем.

.

Подставляем ив уравнение (3), получаем:

,

, (4).

выберем функцию u такой, чтобы .

,

,

интегрируя, получаем

.

Подставляя найденную функцию u в уравнение (4), получаем

,

,

.

Возвращаясь к переменной у, получаем решение исходного уравнения (3)

.

Пример. Решить уравнение: .

Решение: Полагаем , тогда

,

.

Для определения u решаем уравнение

,

,

откуда

,

.

Подставляя u в уравнение , получаем для определенияv уравнение

,

или

,

откуда

.

Следовательно, общий интеграл заданного уравнения будет иметь вид

.

Ответ: .

Дифференциальные уравнения высших порядков, допускающие понижение порядка

1. Уравнение вида 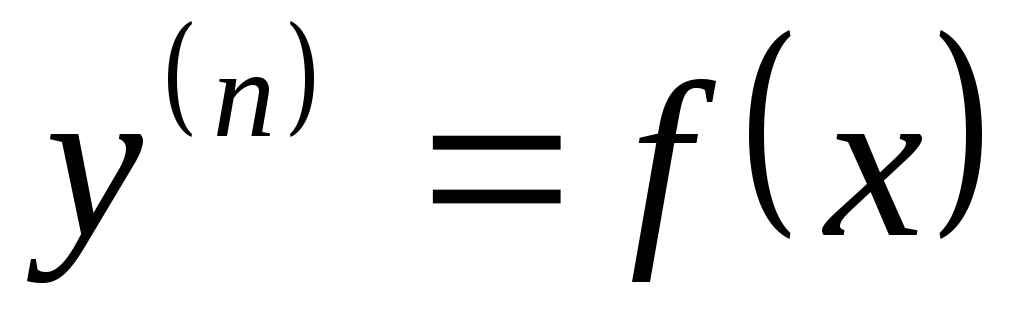решается последовательнымn-кратным интегрированием правой части. При каждом интегрировании получается одно произвольное постоянное, а в окончательном результате – n произвольных постоянных.

Пример. Решить уравнение .

Решение: ,

,

.

Ответ: .

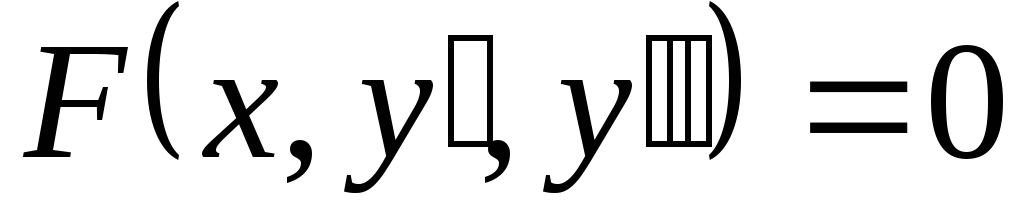2. Уравнение , не содержащееу в явной форме, подстановкой 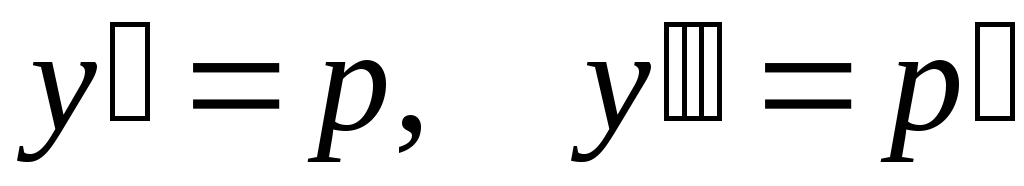приводится к виду

.

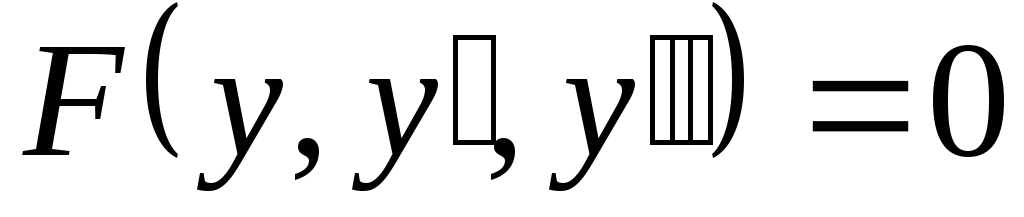3. Уравнение , не содержащеех в явной форме, подстановкой 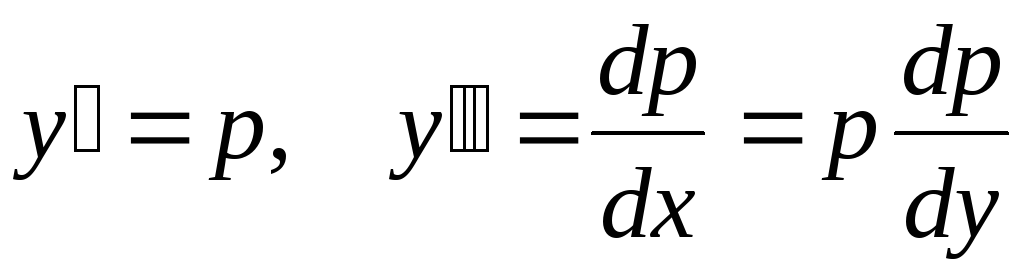приводится к виду

.

Задачи для самостоятельной работы

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

11. .

12. .

27