
- •Производная
- •Производная сложной функции
- •Задачи для самостоятельной работы
- •Неопределенный интеграл
- •Основные свойства неопределенного интеграла
- •Интегрирование по частям Формула интегрирования по частям: .
- •Задачи для самостоятельной работы
- •Дифференциальные уравнения Основные понятия и определения
- •Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения первого порядка с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Дифференциальные уравнения высших порядков, допускающие понижение порядка
- •Задачи для самостоятельной работы
Производная
Определение:
Производной
функции
![]() в точкех
называется предел отношения приращения
функции к приращению аргумента, когда
приращение аргумента стремится к нулю
в точкех
называется предел отношения приращения
функции к приращению аргумента, когда
приращение аргумента стремится к нулю
![]() .
.
Операция нахождения производной называется дифференцированием функции; функция, которая имеет производную в данной точке, называется дифференцируемой в данной точке.
Эквивалентные обозначения производной:
![]() .
.
Основные правила дифференцирования:
1.
![]() .
.
2.
![]()
3.
![]()
4.
![]()
5.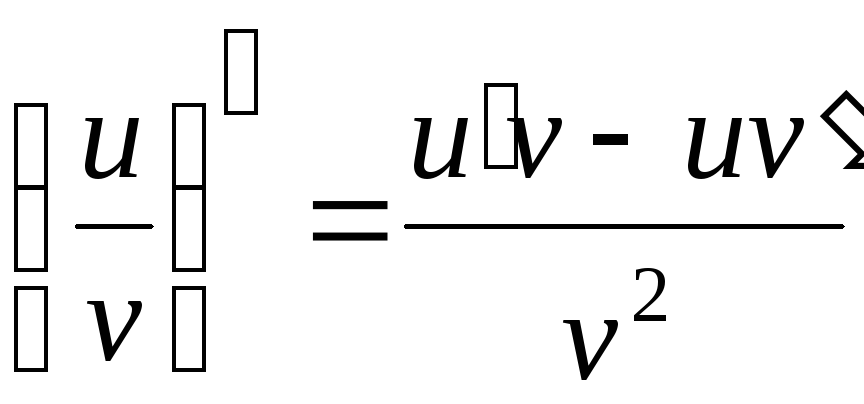
Таблица производных:
1.
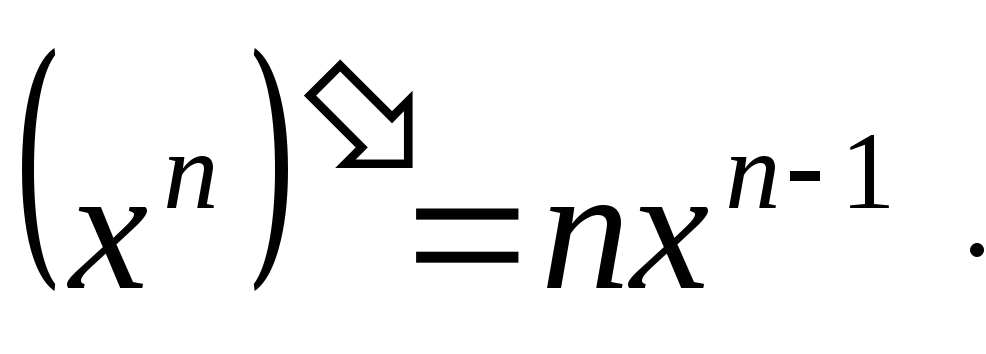
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() .
.
6.
![]() .
.
7.![]() .
.
8.
![]() .
.
9.
![]() .
.
10.
![]() .
.
11.
![]() .
.
12.
![]() .
.
13.
![]() .
.
Пример. Найти
производную функции
![]() .
.
Решение:
![]() .
.
![]()
Пример.
Найти производную функции
![]()
Решение:
![]()
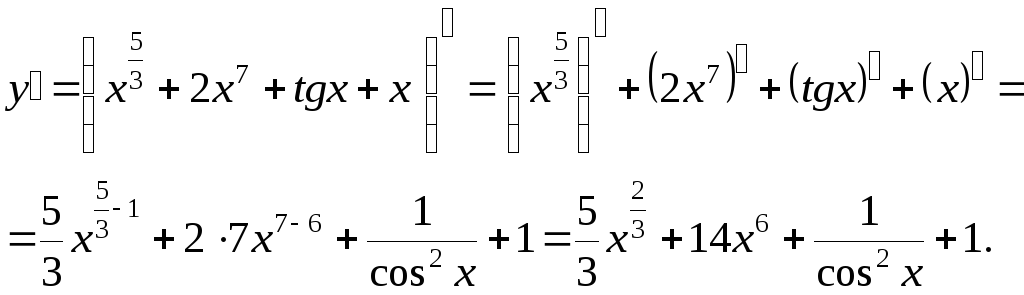
Пример.
Найти производную функции
![]() .
.
Решение:
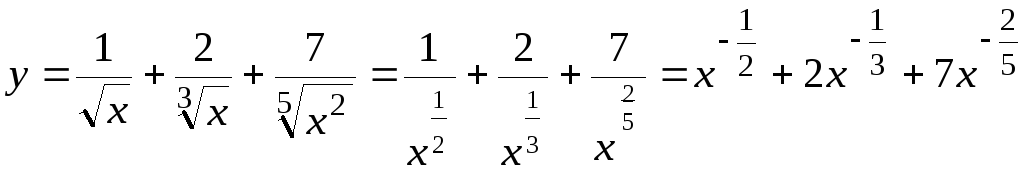 .
.
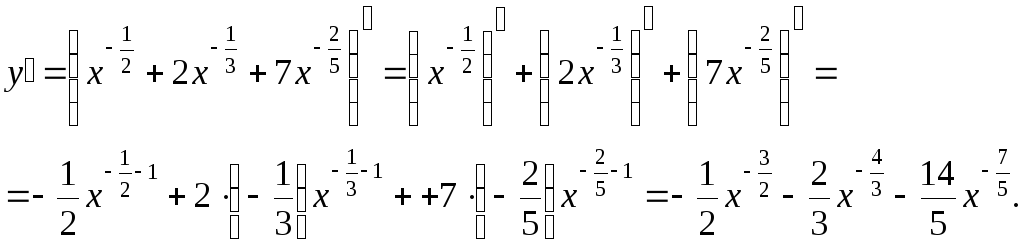
Пример.
Найти
производную функции
![]() .
.
Решение:
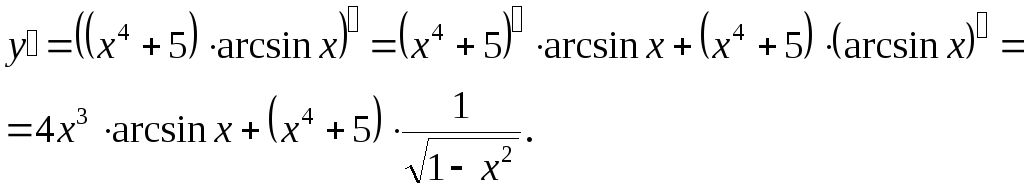
Пример.
Найти
производную функции
![]()
Решение:
![]()
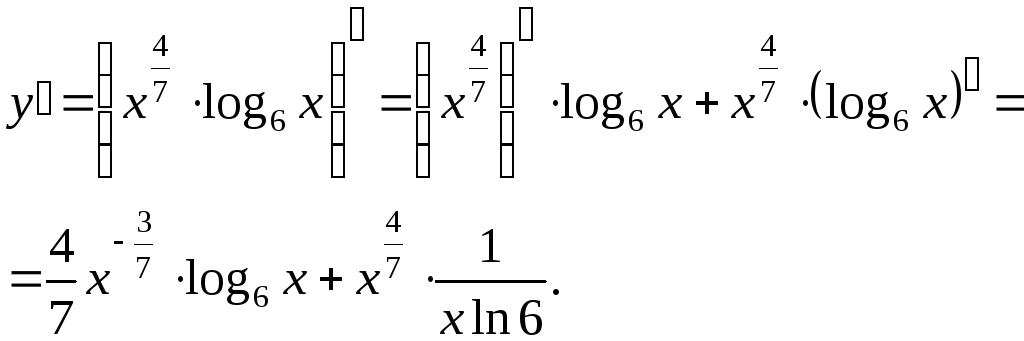
Пример.
Найти
производную функции
![]() .
.
Решение:
![]()
![]()
Пример.
Найти
производную функции
![]() .
.
Решение:
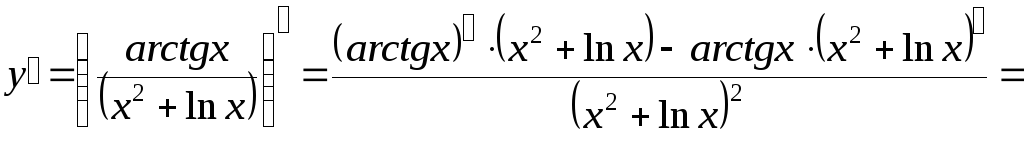

Производная сложной функции
Сложная функция – это функция от функции.
В
записи
![]() x
называется независимой переменной,
x
называется независимой переменной,
u – промежуточным аргументом; u(x) – внутренняя функция;
f – внешняя функция.
Производная сложной функции равна производной от внешней функции по промежуточному аргументу, помноженной на производную внутренней функции:
![]() .
.
Таблица производных для сложных функций:
1.
![]() . 1.1.
. 1.1.![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() .
.
6.
![]() .
.
7.
![]() .
.
8.
![]() .
.
9.
![]() .
.
10.
![]() .
.
11.
![]() .
.
12.
![]() .
.
13.
![]() .
.
Во всех формулах u является некоторой функцией от х.
Пример.
Найти производную функции
![]() .
.
Решение:
Данная
функция является сложной. Её можно
представить в виде цепочки «простых»
функций
![]() ,
где
,
где![]() .
По правилу дифференцирования сложной
функции получаем:
.
По правилу дифференцирования сложной
функции получаем:
![]()
Пример.
Найти
производную функции
![]()
Решение:
![]()
![]()
Пример.
Найти производную функции
![]() .
.
Решение:
![]() .
.
![]()
Пример.
Найти производную функции
![]()
Решение:
![]()
Пример.
Найти производную функции
![]() .
.
Решение:
![]()
Пример.
Найти производную функции
![]()
Решение:
![]()
Пример.
Найти производную функции
![]()
Решение:
![]()
![]()
Пример.
Найти производную функции
![]()
Решение:
![]()
![]()
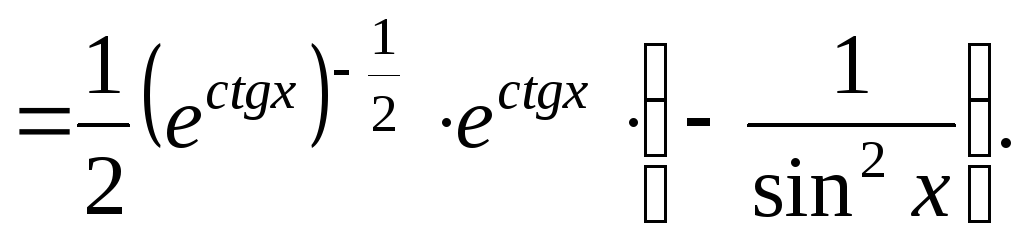
Пример.
Найти производную функции
![]()
Решение:
![]()
![]() =
=
![]()
![]()
Задачи для самостоятельной работы
1–50. Вычислить производные от заданных функций:
Указание: Студентам не рекомендуется увлекаться упрощением выражений, полученных в результате дифференцирования, так как основная цель этой главы заключается в освоении техники дифференцирования, а не в проверке умения производить тождественные преобразования.
1)
![]() . 2)
. 2)
![]() .
.
3)
![]() . 4)
. 4)![]() .
.
5)
![]() . 6)
. 6)
![]() .
.
7)
![]() . 8)
. 8)![]() .
.
9)
![]() . 10)
. 10)![]() .
.
11)
![]() . 12)
. 12)![]() .
.
13)
![]() . 14)
. 14)![]() .
.
15)
![]() . 16)
. 16)![]() .
.
17)
![]() . 18)
. 18)![]() .
.
19)
![]() . 20)
. 20)![]() .
.
21)
![]() . 22)
. 22)![]() .
.
23)
![]() . 24)
. 24)
![]() .
.
25)
![]() . 26)
. 26)![]() .
.
27)
![]() . 28)
. 28)![]() .
.
29)
![]() . 30)
. 30)![]() .
.
31)
![]() . 32)
. 32)![]() .
.
33)
![]() . 34)
. 34)![]() .
.
35)
![]() . 36)
. 36)![]() .
.
37)
![]() . 38)
. 38)![]() .
.
39)
![]() . 40)
. 40)![]() .
.
41)
![]() . 42)
. 42)![]() .
.
43)
![]() . 44)
. 44)![]() .
.
45)
![]() . 46)
. 46)![]() .
.
47)
![]() . .48)
. .48)![]() .
.
49)
![]() . 50)
. 50)![]() .
.
Неопределенный интеграл
Определение:
Неопределенным интегралом
![]() называется функция
называется функция![]() ,
содержащая произвольное постоянноеС,
дифференциал
которой равен
подынтегральному выражению
,
содержащая произвольное постоянноеС,
дифференциал
которой равен
подынтегральному выражению
![]() ,
,
т.е
![]() ,
если
,
если
![]() .
.
Основные свойства неопределенного интеграла
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
Таблица основных интегралов
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() .
.
6.![]() .
.
7.
![]() .
.
8.
![]() .
.
9.
![]() .
.
10.
![]() .
.
11.
![]() .
.
12.
![]() .
.
Непосредственное интегрирование. Вычисление интегралов, основанное на приведении подынтегрального выражения к табличной форме и использовании свойств неопределенного интеграла, называется непосредственным интегрированием.
Примеры: Найти интегралы:
1)
![]() ;
;
2)
![]() .
.
Решение: 1) Разложим подынтегральную функцию на слагаемые, после чего проинтегрируем каждое из полученных слагаемых:
![]()
![]() .
.
2) Разделив почленно числитель на знаменатель, разложим подынтегральную функцию на слагаемые, после чего проинтегрируем каждое из полученных слагаемых:
![]()
=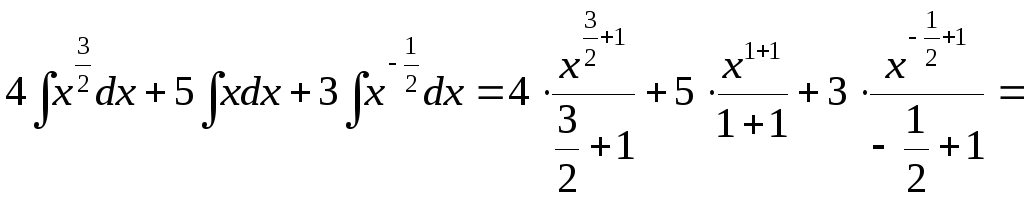
=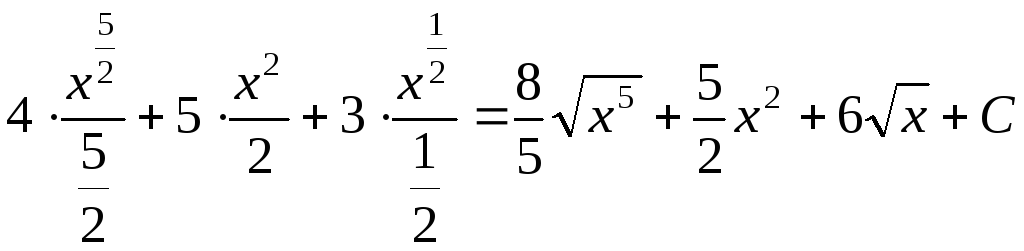 .
.
Интегрирование
подстановкой (заменой переменной). Пусть
требуется вычислить
интеграл
![]() ,
который не является табличным. Суть
метода подстановки состоит в том, что
в интеграле
,
который не является табличным. Суть
метода подстановки состоит в том, что
в интеграле![]() переменнуюх
заменяют
переменной t
по формуле
переменнуюх
заменяют
переменной t
по формуле
![]() ,
откуда
,
откуда![]() .
.
Пример. Найти
интеграл
![]()
Решение: При
нахождении этого интеграла записи самой
подстановки можно не производить. Здесь
достаточно принять во внимание, что
При
нахождении этого интеграла записи самой
подстановки можно не производить. Здесь
достаточно принять во внимание, что
![]() .
Таким образом,
.
Таким образом,
![]()
Пример. Найти
интеграл
![]()
Решение:

или заметим, что
![]() ,
тогда
,
тогда
![]()
Пример. Найти
интеграл
![]()
Решение:
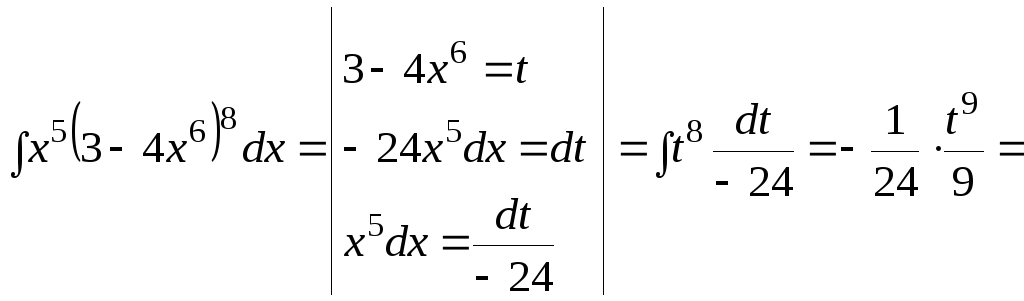
![]()
или заметим, что
![]() ,
тогда
,
тогда
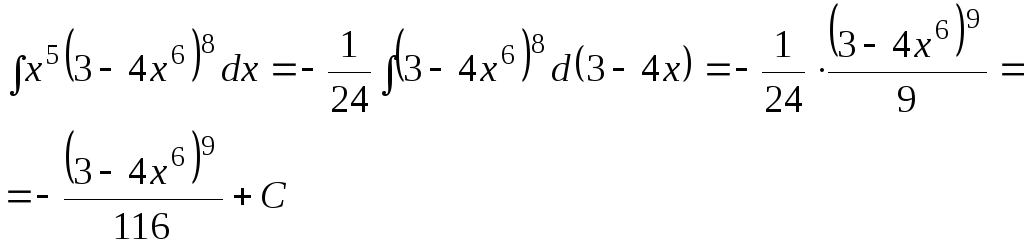
Пример.
Найти интеграл
![]()
Решение:
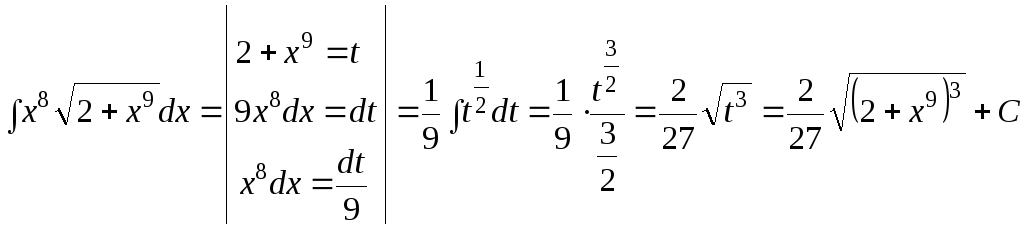
или заметим, что
![]() ,
тогда
,
тогда
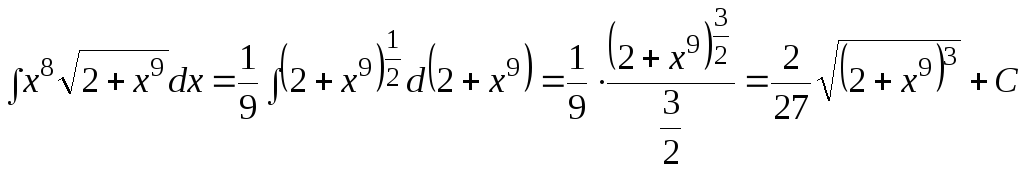
Пример. Найти
интеграл
![]()
Решение:
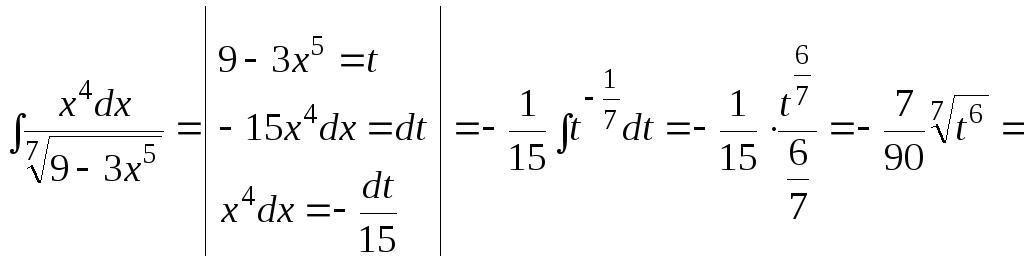
![]()
или заметим, что
![]() ,
тогда
,
тогда
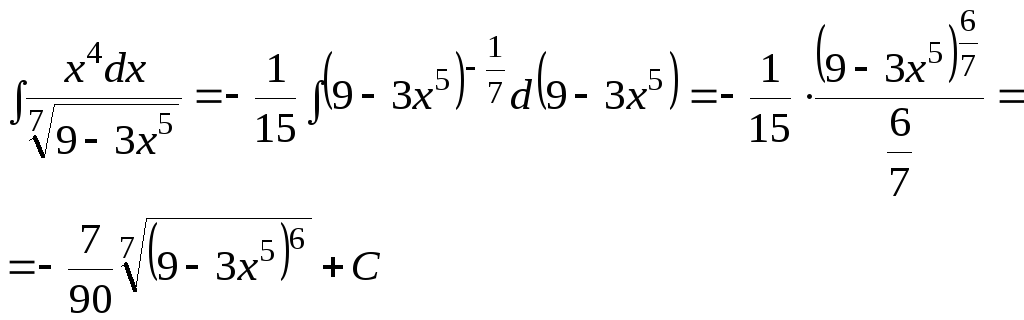
![]()
Пример. Найти
интеграл
![]()
Решение: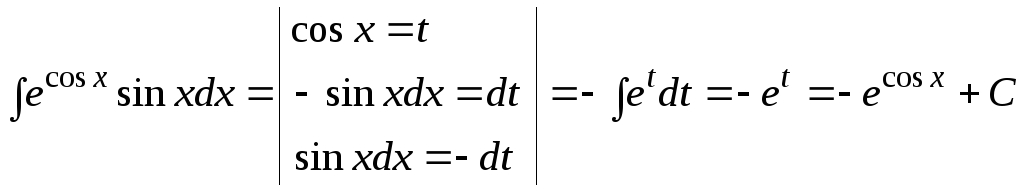
или заметим, что
![]() ,
тогда
,
тогда
![]()
Пример.
Найти интеграл
![]()
Решение:
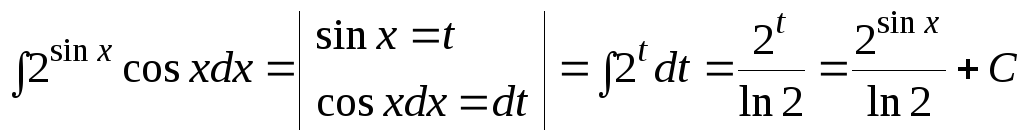
или заметим, что
![]() ,
тогда
,
тогда
![]()
