
Глава 10
Міра Лебега
3. Вимірні множини
Нехай
як і раніше
![]() - основний простір, A
- деяка алгебра, на якій визначена міра
- основний простір, A
- деяка алгебра, на якій визначена міра![]() ,
,
![]() - зовнішня міра, що визначається за
формулою (2.1)
- зовнішня міра, що визначається за
формулою (2.1)
![]() .
Більшість з наведених далі тверджень
справджуються для будь-яких мір, для
доведення інших треба звузити клас мір
.
Більшість з наведених далі тверджень
справджуються для будь-яких мір, для
доведення інших треба звузити клас мір
![]() скінченими.
скінченими.
Множина
![]() називається вимірною
(ВМ)
(вимірною
за Каратеодорі),
якщо
називається вимірною
(ВМ)
(вимірною
за Каратеодорі),
якщо
![]() виконується рівність:
виконується рівність:
![]() (1)
(1)
Оскільки
![]() ,
а тому з напівадитивності зовнішньої
міри маємо, що
,
а тому з напівадитивності зовнішньої
міри маємо, що
![]() ,
тобто для доведення вимірності деякої
множини треба перевіряти лише зворотну
нерівність.
,
тобто для доведення вимірності деякої
множини треба перевіряти лише зворотну
нерівність.
Сукупність
усіх вимірних множин позначимо A,
а звуження зовнішньої міри
![]() на A
позначимо
на A
позначимо
![]() .
.
|
Теорема 1. |
(Сукупність вимірних множин) |
|
|
Сукупність
A
вимірних множин утворює
|
Доведення проводиться в декілька кроків.
Першій
крок.
Покажемо, що з умови
![]() A,
то й
A,
то й
![]() A.
Дійсно, оскільки множина
A.
Дійсно, оскільки множина
![]() - ВМ, то
- ВМ, то
![]() виконується (1).
Запишемо його, замінюючи
виконується (1).
Запишемо його, замінюючи
![]() на
на
![]() ,
а далі на
,
а далі на
![]() :
:
![]() , (2)
, (2)
![]() . (3)
. (3)
Додамо
останні дві нерівності, тоді з вимірності
![]() зліва одержимо
зліва одержимо
![]() ,
а тому маємо
,
а тому маємо
![]() :
:
![]()
![]() (4)
(4)
В
останній рівності, що справджується
![]() замінимо
замінимо
![]() на
на
![]() .
Перші три доданки правої частини (4)
не зміняться при такій заміні, а останній
доданок стане дорівнювати:
.
Перші три доданки правої частини (4)
не зміняться при такій заміні, а останній
доданок стане дорівнювати:
![]() ,
а тому остаточно одержимо:
,
а тому остаточно одержимо:
![]()
![]() (5)
(5)
Порівнюючи
(4),(5),
одержимо, що
![]() :
:
![]()
тобто
множина
![]() - вимірна.
- вимірна.
Другий
крок.
Оскільки при заміні
![]() на
на
![]() рівність (1)
не змінюється, а тому з вимірності
рівність (1)
не змінюється, а тому з вимірності
![]() слідує й вимірність
слідує й вимірність
![]() .
З перших двох пунктів слідує, що A
- алгебра.
.
З перших двох пунктів слідує, що A
- алгебра.
Третій
крок.
Якщо
![]() - диз’юнктна система, то рівність (5)
набуває вигляду:
- диз’юнктна система, то рівність (5)
набуває вигляду:
![]() ,
аналогічно для будь-якої скінченої
диз’юнктної
системи множин
,
аналогічно для будь-якої скінченої
диз’юнктної
системи множин
![]() :
:
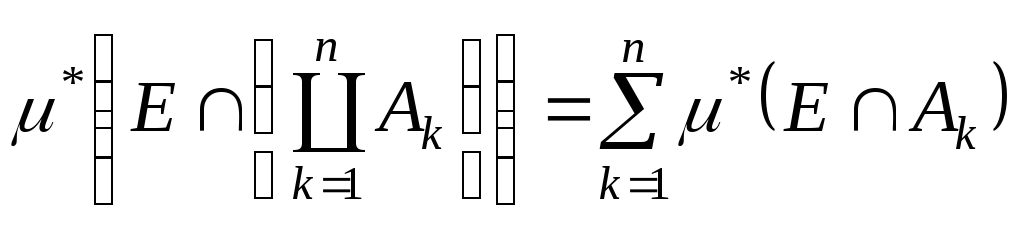 . (6)
. (6)
Четвертий
крок.
Доведемо, що A
-
![]() алгебра.
Нехай нам задана довільна послідовність
множин
алгебра.
Нехай нам задана довільна послідовність
множин
![]() A,
яку без обмеження загальності ми можемо
вважати диз’юнктною.
Для доведення вимірності їх об’єднання
достатньо показати, що виконується
нерівність
A,
яку без обмеження загальності ми можемо
вважати диз’юнктною.
Для доведення вимірності їх об’єднання
достатньо показати, що виконується
нерівність
![]() :
:
![]() . (7)
. (7)
З
того, що A
-
алгебра зрозуміло, що
![]()
 A,
тому:
A,
тому:
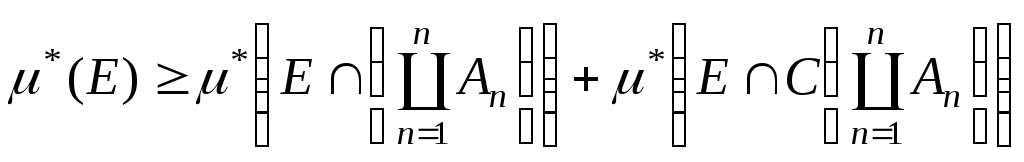 ,
,
з формули (6) та з монотонності зовнішньої міри одержимо:
 , (8)
, (8)
тут
ми використали очевидне включення
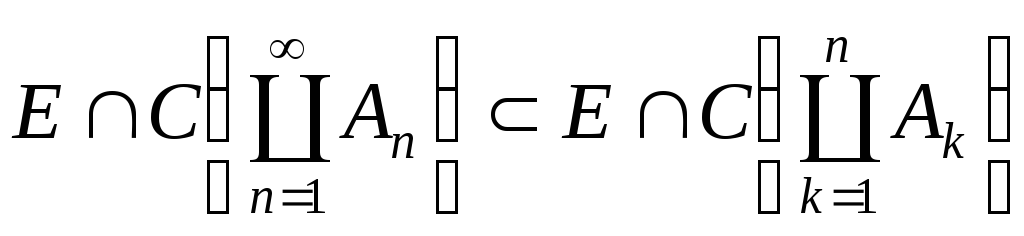 ,
що справджується
,
що справджується
![]() ,
переходимо до границі при
,
переходимо до границі при
![]() ,
знайдемо:
,
знайдемо:
![]() . (9)
. (9)
Із зліченої напівадитивності ЗМ, одержимо
![]() ,
,
додаючи
до цієї нерівності (9),
одержимо (7),
тому
![]() A,
тобто A
-
A,
тобто A
-
![]() алгебра.
алгебра.
П’ятий
крок.
Доведемо, що
![]() на A
є мірою. Для цього достатньо показати
злічену адитивність
на A
є мірою. Для цього достатньо показати
злічену адитивність
![]() на A.
Нехай
на A.
Нехай
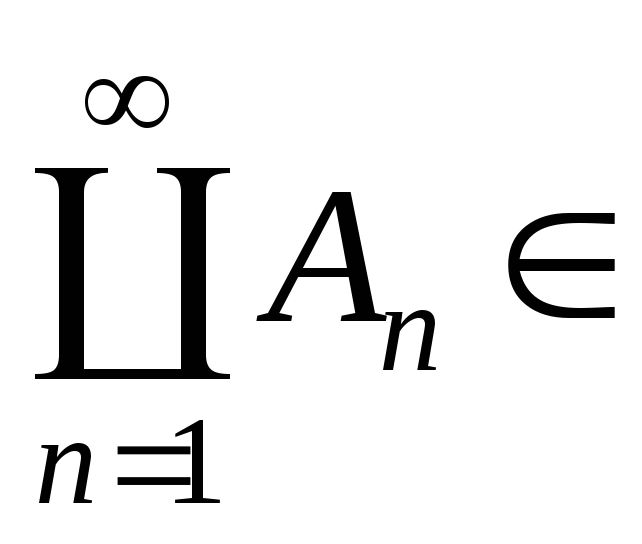 A.
Покладемо в (9)
A.
Покладемо в (9)
![]() ,
тоді будемо мати
,
тоді будемо мати
![]() ,
поєднуючи це з зліченою напівадитивністю,
одержимо потрібну рівність:
,
поєднуючи це з зліченою напівадитивністю,
одержимо потрібну рівність:
![]() .
.
Шостий
крок.
Доведемо, що A![]() A.
Для цього достатньо показати, що
A.
Для цього достатньо показати, що
![]() A
ця множина – вимірна, тобто виконується
нерівність
A
ця множина – вимірна, тобто виконується
нерівність
![]() :
:
![]() . (10)
. (10)
З
визначення зовнішньої міри та властивостей
інфінума:
![]()
![]() A:
A:
![]() ,
при цьому
,
при цьому
![]() . (11)
. (11)
Кожну
з множин подамо у вигляді:
![]() ,
кожна множина цього об’єднання
входить в A,
тому й
,
кожна множина цього об’єднання
входить в A,
тому й
![]() ,
,
тоді нерівність (11) набуває вигляду:
![]() . (12)
. (12)
Крім того,
![]() ,
,
![]() ,
,
звідки означенню зовнішньої міри, маємо:
![]() ,
,
![]()
а
тому з (12)
одержимо:
![]()
Внаслідок
довільності
![]() одержуємо те, що треба.
одержуємо те, що треба.
Теорема доведена.
|
Теорема 2. |
(Існування продовження міри) |
|
|
Нехай
A
- деяка алгебра,
|
Доведення.
Все безпосередньо слідує з попередньої
теореми. Побудуємо по мірі
![]() зовнішню міру
зовнішню міру
![]() і за A1
виберемо
і за A1
виберемо
![]() алгебру
A
усіх вимірних (за Каратеодорі) множин,
а за
алгебру
A
усіх вимірних (за Каратеодорі) множин,
а за
![]() - міру
- міру
![]() .
Це й буде шуканим продовженням міри.
.
Це й буде шуканим продовженням міри.
Теорема доведена.
Нехай
A
- деяка алгебра,
![]() - міра на A.
Позначимо A
- міра на A.
Позначимо A![]() породжену цією алгеброю
породжену цією алгеброю
![]() алгебру
(мінімальну), побудуємо продовження
алгебру
(мінімальну), побудуємо продовження
![]() міри
міри
![]() на A
на A![]() .
Таке продовження називають мінімальним
продовженням.
.
Таке продовження називають мінімальним
продовженням.
Легко
показати, що воно існує. Оскільки A![]()
![]() A,
то можемо покласти
A,
то можемо покласти
![]() ,
як звуження міри
,
як звуження міри
![]() на
на
![]() алгебру
A
алгебру
A![]() .
Очевидно, що
.
Очевидно, що
![]() міра і що це мінімальне продовження
міри
міра і що це мінімальне продовження
міри
![]() .
.
Якщо
![]() - аксіоматично визначена зовнішня міра,
то для неї можна визначити аналогічним
чином поняття вимірності та вимірної
множини. При цьому залишається чинною
теорема 1.
- аксіоматично визначена зовнішня міра,
то для неї можна визначити аналогічним
чином поняття вимірності та вимірної
множини. При цьому залишається чинною
теорема 1.
Міра
![]() ,
що задана на алгебрі A,
називається повною,
якщо з умов
,
що задана на алгебрі A,
називається повною,
якщо з умов
![]() A,
A,
![]() ,
,
![]() слідує, що
слідує, що
![]() A.
Зрозуміло, з монотонності міри, що при
цьому
A.
Зрозуміло, з монотонності міри, що при
цьому
![]() .
.
|
Теорема 3. |
(Про множини нульової міри) |
|
|
Нехай
|
Доведення.
Для доведення вимірності достатньо
показати, що справджується нерівність:
![]() ,
,
![]() .
Оскільки
.
Оскільки
![]() ,
то з монотонності та невід’ємності
міри слідує
,
то з монотонності та невід’ємності
міри слідує
![]()
![]()
![]() ,
аналогічно
,
аналогічно
![]()
![]()
![]() ,
тобто множина
,
тобто множина
![]() вимірна, а далі очевидно, що
вимірна, а далі очевидно, що
![]() .
.
Теорема доведена.
|
Наслідок. |
(Повнота
міри
|
|
|
Міра
|
|
Теорема 4. |
(Неперервність знизу) |
|
|
Нехай
|
Доведення.
Згадавши подання об’єднання
через диз’юнктні
множини, одержимо:
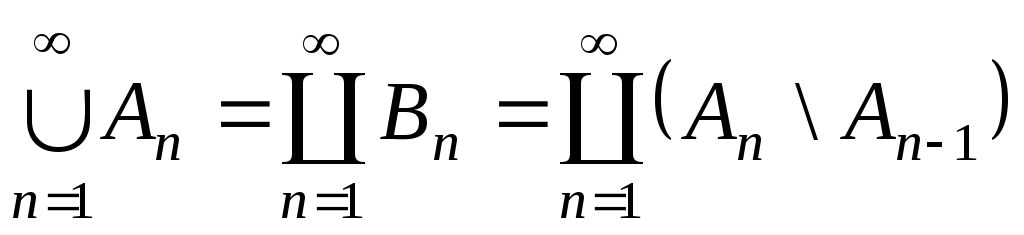
![]()
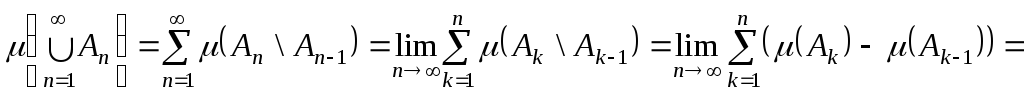
![]() ,
,
з
урахуванням того, що
![]() .
.
Теорема доведена.
|
Теорема 5. |
(Неперервність зверху) |
|
|
Нехай
|
Доведення.
Без обмежень загальності можемо вважати,
що
![]() (тобто скінчена), а тому далі за правилами
де Моргана легко зведемо задачу до
попередньої:
(тобто скінчена), а тому далі за правилами
де Моргана легко зведемо задачу до
попередньої:
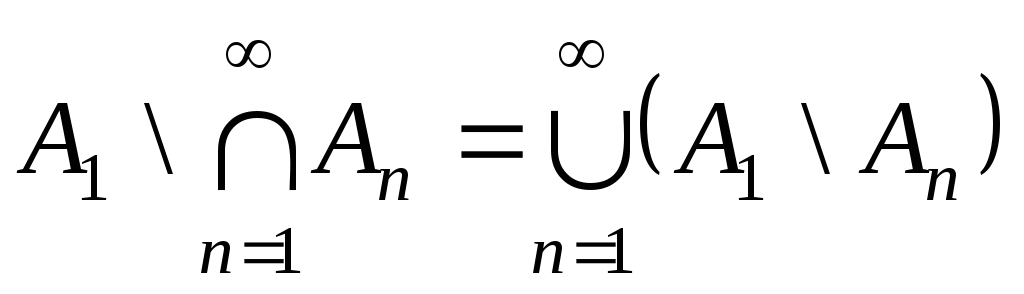 ,
з субтрактивності міри
,
з субтрактивності міри
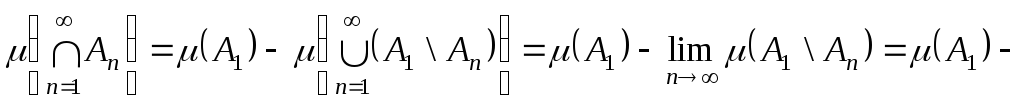
![]() ,
що й треба довести.
,
що й треба довести.
Теорема доведена.
|
Теорема 6. |
(Критерій вимірності) |
|
|
Нехай
|
Доведення.
Необхідність.
З того, що
![]() A
останню умову можна записати у вигляді
A
останню умову можна записати у вигляді
![]() .
Нехай
множина
.
Нехай
множина
![]() має скінчену міру. З визначення зовнішньої
міри
має скінчену міру. З визначення зовнішньої
міри
![]()
![]() A:
A:
![]() і
і
![]() . (13)
. (13)
Оскільки
![]() та
та
![]() ,
то останню нерівність можна переписати
у вигляді:
,
то останню нерівність можна переписати
у вигляді:
![]() .
.
Запишемо
![]() ,
справа записана монотонно зростаюча
послідовність множин, то з теореми 4
,
справа записана монотонно зростаюча
послідовність множин, то з теореми 4
![]() ,
із збіжності ряду
,
із збіжності ряду
![]() можемо вибрати
можемо вибрати
![]() достатньо великим, щоб виконувалась
нерівність:
достатньо великим, щоб виконувалась
нерівність:
![]() , (14)
, (14)
тоді
покладемо
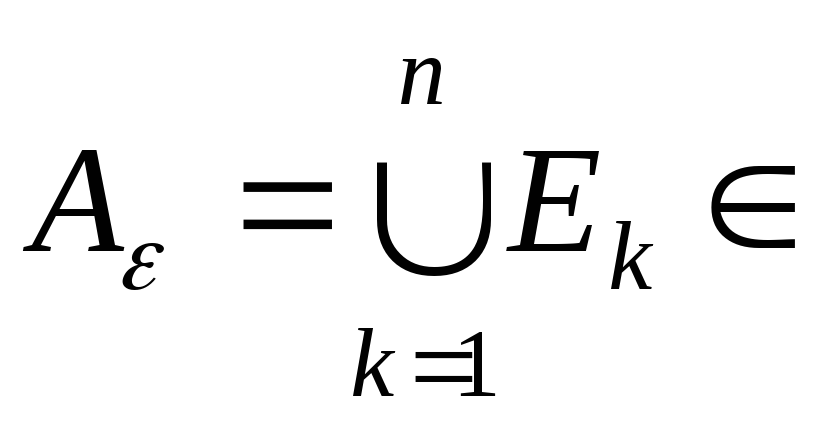 A
і покажемо, що воно шукане, тобто
виконується нерівність
A
і покажемо, що воно шукане, тобто
виконується нерівність
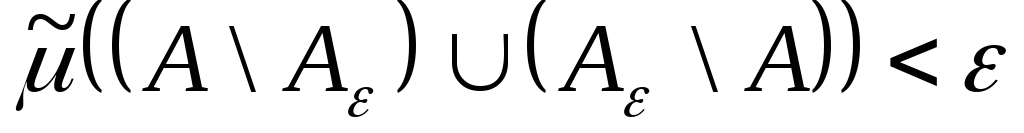 ,
для чого достатньо щоб виконувалися
нерівності:
,
для чого достатньо щоб виконувалися
нерівності:
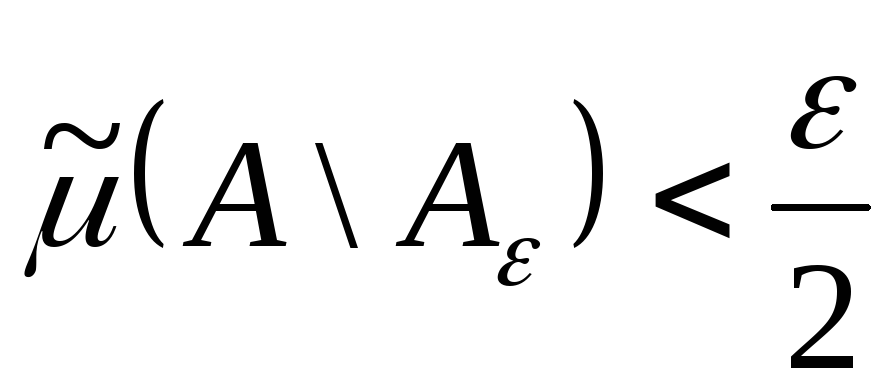 , (15.1)
, (15.1)
![]() . (15.2)
. (15.2)
Оскільки
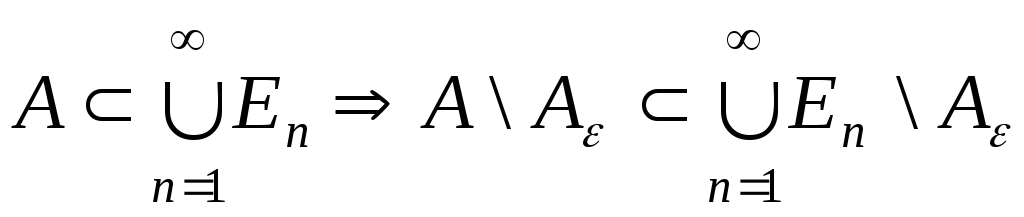 ,
тому з монотонності, субтрактивності
міри та з формули (14)
маємо:
,
тому з монотонності, субтрактивності
міри та з формули (14)
маємо:
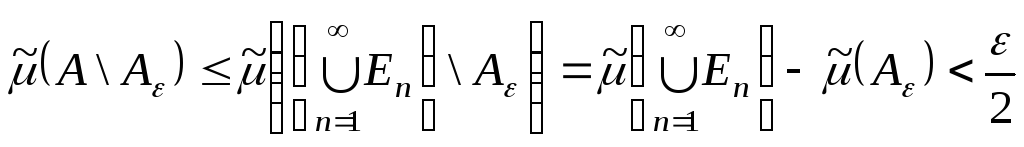 ,
і нерівність (15.1)
доведена. Далі, оскільки
,
і нерівність (15.1)
доведена. Далі, оскільки
![]() ,
то з властивостей міри:
,
то з властивостей міри:
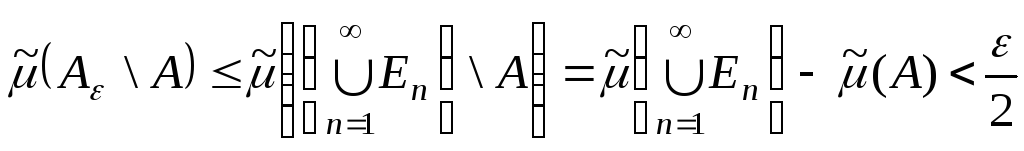 ,
що слідує із співвідношення (13).
Таким чином доведена нерівність (15.2),
а тому й необхідність
доведена.
,
що слідує із співвідношення (13).
Таким чином доведена нерівність (15.2),
а тому й необхідність
доведена.
Достатність.
Для
скінченої міри усе доводиться доволі
просто. Якщо
![]() - вимірна за Каратеодорі, то
- вимірна за Каратеодорі, то
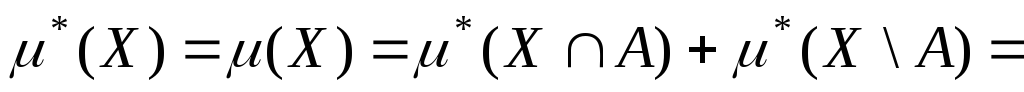
![]()
![]() ,
а тому
,
а тому
![]() ,
що еквівалентно вимірності за Лебегом.
Інші випадки цієї теореми пропонуємо
довести самостійно.
,
що еквівалентно вимірності за Лебегом.
Інші випадки цієї теореми пропонуємо
довести самостійно.
Теорема доведена.
Система
M
підмножин простору
![]() називається монотонним
класом,
якщо разом з будь-якою монотонною
послідовністю множин
називається монотонним
класом,
якщо разом з будь-якою монотонною
послідовністю множин
![]() вона містить також її границю
вона містить також її границю
![]() .
.
|
Лема 1. |
(Кільце – монотонний клас) |
|
|
Якщо
кільце множин R
є монотонним класом, то R
-
|
Доведення.
Виберемо довільну послідовність множин
![]() R,
побудуємо монотонно зростаючу
послідовність множин
R,
побудуємо монотонно зростаючу
послідовність множин
![]() ,
з того, що R
- монотонний клас, слідує, що
,
з того, що R
- монотонний клас, слідує, що
![]() R,
що й треба було довести.
R,
що й треба було довести.
Лема доведена.
|
Теорема 7. |
(Про мінімальний монотонний клас) |
|
|
Нехай
R
- деяке кільце. Позначимо через R |
Доведення.
Оскільки R![]() містить усі можливі злічені об’єднання,
а R
містить усі можливі злічені об’єднання,
а R![]() лише об’єднання монотонних послідовностей,
то R
лише об’єднання монотонних послідовностей,
то R![]() R
R![]() .
Якщо ми покажемо, що R
.
Якщо ми покажемо, що R![]() - кільце множин, то з леми одержимо, що
R
- кільце множин, то з леми одержимо, що
R![]() - також
- також
![]() -кільце.
Тоді оскільки R
-кільце.
Тоді оскільки R![]() - мінімальне
- мінімальне
![]() -кільце,
що містить R,
то R
-кільце,
що містить R,
то R![]() R
R![]() ,
з чого й буде слідувати потрібна рівність.
Тобто залишається показати, що R
,
з чого й буде слідувати потрібна рівність.
Тобто залишається показати, що R![]() - кільце множин.
- кільце множин.
Першій
крок.
Зафіксуємо множину
![]() та розглянемо клас множин
та розглянемо клас множин
![]() R
R![]()
![]() .
З симетричності визначення відносно
.
З симетричності визначення відносно
![]() слідує, що з умови
слідує, що з умови
![]() слідує
слідує
![]() .
.
Другий
крок.
Покажемо, що
![]() - монотонний клас. Нехай дана зростаюча
послідовність множин
- монотонний клас. Нехай дана зростаюча
послідовність множин
![]() ,
покажемо, що
,
покажемо, що
![]() .
З означення границі зростаючої
послідовності:
.
З означення границі зростаючої
послідовності:
![]() R
R![]() ,
аналогічно
,
аналогічно
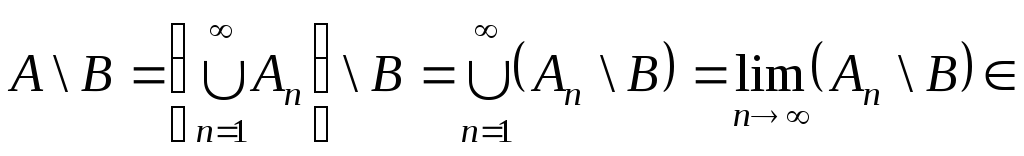 R
R![]() і
і
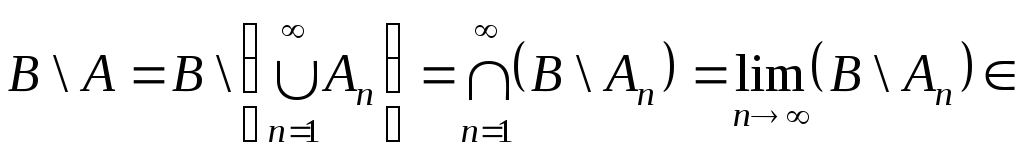 R
R![]() ,
оскільки послідовність
,
оскільки послідовність
![]() - спадна з монотонного класу R
- спадна з монотонного класу R![]() .
Тому
.
Тому
![]() .
Повністю аналогічно цеж саме перевіряється
для монотонно спадної послідовності
.
Повністю аналогічно цеж саме перевіряється
для монотонно спадної послідовності
![]() ,
тобто, що й
,
тобто, що й
![]() .
Тому
.
Тому
![]() - монотонний клас.
- монотонний клас.
Третій
крок.
Нехай
![]() R.
Покажемо, що R
R.
Покажемо, що R![]()
![]() .
Спочатку покажемо, що R
.
Спочатку покажемо, що R![]() .
Нехай
.
Нехай
![]() R.
З того, що R
- кільце слідує, що
R.
З того, що R
- кільце слідує, що
![]() R,
а тому й
R,
а тому й
![]() R
R![]() ,
тобто
,
тобто
![]() .
Таким чином R
.
Таким чином R![]() ,
тобто
,
тобто
![]() - монотонний клас, що містить R.
Оскільки R
- монотонний клас, що містить R.
Оскільки R![]() - мінімальний подібний клас, то R
- мінімальний подібний клас, то R![]()
![]() .
.
Четвертий
крок.
Якщо
![]() R
R![]() ,
то R
,
то R![]()
![]() .
Для доведення візьмемо довільну множину
.
Для доведення візьмемо довільну множину
![]() R,
тоді за доведеним на третьому кроці
одержимо, що R
R,
тоді за доведеним на третьому кроці
одержимо, що R![]()
![]() .
Оскільки
.
Оскільки
![]() R
R![]() ,
то
,
то
![]() ,
то з доведеного на першому кроці
,
то з доведеного на першому кроці
![]() .
Таким чином R
.
Таким чином R![]() ,
а тому й R
,
а тому й R![]()
![]() .
.
П’ятий
крок.
Покажемо тепер заключне, що R![]() - кільце. Нехай
- кільце. Нехай
![]() R
R![]() .
Оскільки
.
Оскільки
![]() R
R![]() ,
то з доведеного на четвертому кроці
R
,
то з доведеного на четвертому кроці
R![]()
![]() ,
зокрема
,
зокрема
![]() .
Але тоді з визначення слідує, що
.
Але тоді з визначення слідує, що
![]() R
R![]() ,
тобто R
,
тобто R![]() - кільце.
- кільце.
Теорема доведена.
|
Теорема 8. |
(Про єдиність мінімального продовження міри) |
|
|
Нехай
A
- деяка алгебра, A |
Доведення.
Треба показати, що
![]() A
A![]() :
:
![]() .
Якщо
.
Якщо
![]() A,
то це слідує з умов теореми. Якщо
A,
то це слідує з умов теореми. Якщо
![]() A,
то
A,
то
![]() A
A![]()
![]() A
A![]() .
Тому A
є границею монотонної послідовності
.
Тому A
є границею монотонної послідовності
![]() A,
з теорем, про границю монотонних
послідовностей одержимо, що
A,
з теорем, про границю монотонних
послідовностей одержимо, що
![]() .
.
Теорема доведена.
