Lektsii_Rubleva / Лекции Рублева-1 / Гл 10 М_ра Лебега / Пар 10-4 М_ра Лебега в Rm

5

Глава 10

Міра Лебега

4. Міра Лебега в

Нехай - деякий фіксований півінтервал, - півкільце усіх півінтервалів з , A - кільцева оболонка множини (породжене кільце), тобто елемент алгебри A має вигляд:

. (1)

Довжина півінтервалів , , сегменту та інтервалу дорівнює . Довжиною множини , що визначена формулою (1) вважають сумарну довжину проміжків, що її складають, тобто:

.

Теорема 1.	(Визначення міри на алгебрі проміжків)
	Якщо визначити на алгебрі A функцію , поклавши , то вона є мірою цій алгебрі.

Доведення. Очевидними є властивості , а також A . Залишається перевірити адитивність.

Нехай A: 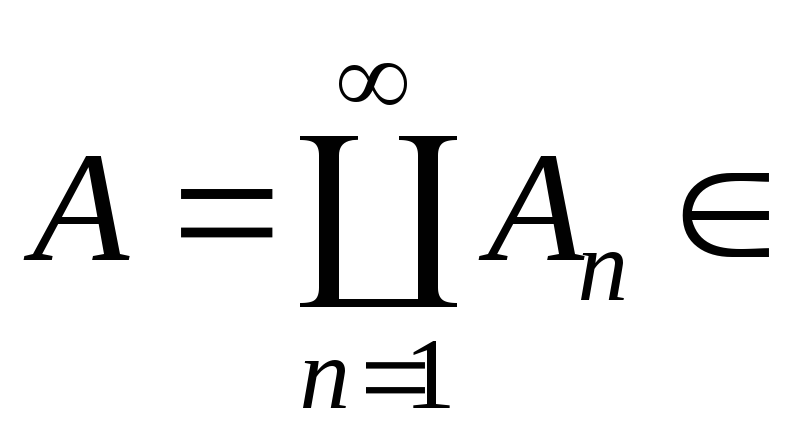A. Треба показати, що

. (2)

Оскільки A, то є об’єднанням скінченої кількості півінтервалів, тому , переходячи до границі, одержимо:

. (3)

Доведемо протилежну нерівність. зсунемо кінці півінтервалів тих проміжків, що складають множину вліво настільки, щоб для об’єднання одержаних замкнених проміжків виконувалась умова:

. (4)

Далі для кожної з множин зсунемо вліво ліві кінці тих півінтервалів, що її складають, та позначимо як об’єднання одержаних відкритих проміжків. При цьому зсуви підбираємо настільки малими, щоб виконувалась умова

. (5)

Оскільки , то , тобто компакт покритий відкритими множинами , а тому з леми Гейне-Бореля з цього покриття можна виділити скінчене підпокриття, тобто для деякого , а для скінченої кількості проміжків маємо: , з чого остаточно одержимо:

, що й треба було довести.

Теорема доведена.

Нехай - зовнішня міра, що побудована для визначеної в теоремі 1 міри ; -вимірні множини називають вимірними за Лебегом, а продовження міри на алгебру AA вимірних за Лебегом множин називають мірою Лебега.

Теорема 2.	(Міра одно точкової множини)
	Множина, що складається з однієї точки, вимірна, та має міру нуль.

Доведення. Достатньо показати, що , де . З визначення зовнішньої міри

.

Теорема доведена.

Теорема 3.	(Міра зліченої множини)
	Довільна не більш як злічена множина точок на прямій вимірна та має міру нуль.

Доведення безпосередньо слідує з того, що множина вимірних множин є алгеброю, а міра Лебега - адитивна.

Теорема 4.	(Міра проміжку)
	Будь-який проміжок є вимірною множиною, та його міра дорівнює його довжині.

Доведення. Для сегменту: , аналогічно для інших типів проміжків.

Теорема доведена.

Теорема 5.	(Вимірність відкритих та замкнених множин)
	Будь-яка відкрита та замкнена множина вимірна за Лебегом.

Доведення. Із структури відкритої множини на будь-яку відкриту множину можна подати у вигляді:

. (6)

Оскільки інтервали вимірні за Лебегом, то й A.

Нехай тепер - замкнена множина, тоді якщо , то - відкрита множина, а тому - вимірна.

Теорема доведена.

Наслідок.	(Міра відкритих та замкнених множин)
	Для множини , що визначається формулою (6) можемо записати , відповідно, .

Борелевською алгеброю в просторі називається алгебра B, що породжена усіма відкритими множинами. Елементи цієї алгебри називаються борелевськими множинами.

Теорема 6.	(Вимірність борелевських множин)
	Будь-яка борелевська множина на прямій вимірна за Лебегом.

Доведення. Відкриті множини входять до алгебри вимірних множин, а B - найменша алгебра, що їх містить.

Теорема доведена.

Теорема 7.	(Необхідна умова вимірності)
	Якщо - вимірна множина на прямій, то існує така обмежена відкрита множина , що та .

Доведення. Оскільки - вимірна, то , а тому , для якого та

. (8)

Для кожного проміжку розглянемо відкритий проміжок , де , та покладемо - відкрита множина. Покажемо, що вона шукана. Зрозуміло, що , далі: 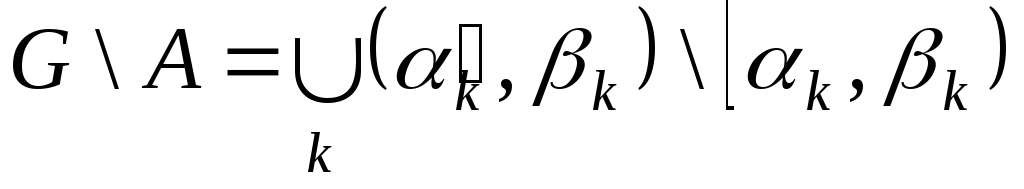, звідки з субтрактивності міри , додаючи сюди (8), одержимо: , тому та .

Теорема доведена.

Тепер продовжимо визначення міри Лебега не лише для обмежених множин на прямій.

Множина називається вимірною за Лебегом, якщо буде вимірним за Лебегом множина .Сукупність усіх вимірних за Лебегом множин позначимо A. Легко зрозуміти з попереднього, що борелевські множини вимірні за Лебегом.

Теорема 8.	(Сукупність вимірних за Лебегом множин)
	Сукупність A вимірних за Лебегом множин утворює алгебру.

Доведення. A, тому що множина - обмежена вимірна множина. Нехай A, тоді множина 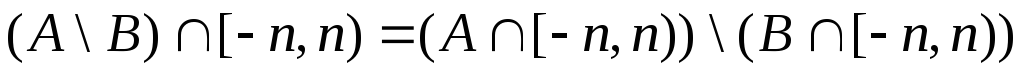- вимірна., тому A. Нехай A, тоді множина - обмежена вимірна множина, тому , тобто A - алгебра.

Теорема доведена.

Мірою Лебега множини A називається границя (можливо нескінченна) .

Зрозуміло, що послідовність є невід’ємною та неспадною, а тому вказана границя обов’язково існує. Покажемо, що визначена функція є скінченою мірою на алгебрі A вимірних множин.

Теорема 9.	(Перевірка міри)
	Визначена функція є скінченною мірою на алгебрі A вимірних множин.

Доведення. Невід’ємність та умова очевидні. Нехай A - диз’юнктна система. Тоді з означення

. Переходячи до границі, що можливо внаслідок невід’ємності членів ряду, одержимо: , доведена адитивність, тому - міра. Оскільки і усі доданки мають скінчену міру, тому - скінчена міра.

Теорема доведена.

Теорема 10.	(Система вичерпних півінтервалів)
	Вимірність множини та значення міри Лебега не залежить від вибору системи пів інтервалів, що монотонно зростають та вичерпують усю дійсну вісь, тобто замість півінтервалів можна вибрати довільну систему півінтервалів таких, що , при цьому сукупність вимірних множин та їх міри не зміняться.

Без доведення.

Міра Лебега в просторі будується за аналогічною схемою, що й в одновимірному просторі.

Нехай дві точки , задовольняють умови . Тоді назвемо - вимірним півінтервалом (або напіввідкритим брусом) множину , об’ємом такого бруса назвемо число .

Легко переконатися, що сукупність таких півінтервалів в -вимірному евклідовому просторі утворює півкільце . Якщо зафіксувати один подібний напіввідкритий брус, то можна утворити алгебру A, що породжена , а тому кожна множина цієї алгебри набуває вигляду: , , об’ємом такої множини будемо вважати суму об’ємів брусів, що його утворюють.

Теорема 11.	(Визначення міри в )
	Якщо A покласти , то - міра.

Доведення аналогічно одновимірному випадку.

Далі так само будується зовнішня міра , визначається клас - вимірних множин, які називаються вимірними за Лебегом, а продовження міри називається мірою Лебега.

Обмежений многовид , , називається регулярним, якщо існує скінчена сукупність півінтервалів , що покриває і така, що .

Так, наприклад, для регулярності - вимірного многовиду достатньо, щоб його можна було задати рівнянням вигляду: , де визначена та неперервна на деякому компакті.

Теорема 12.	(Міра регулярного многовиду)
	Якщо - обмежений регулярний многовид в просторі , розмірності менше за , то - вимірна за Лебегом та .

Доведення безпосередньо слідує з означення регулярності, тому що .

Для необмежених множин також усе визначається аналогічно визначенню міри для необмежених множин на прямій.