Lektsii_Rubleva / Лекции Рублева-1 / Гл 11 М_ра Лебега / Пар 12_3 Прост_ функц_ї теорема Луз_на

Глава 12.

ВИМІРНІ ФУНКЦІЇ.

ІНТЕГРАЛ ЛЕБЕГА.

12.3. Прості функції. Теорема Лузіна.

Числова функція , що визначена на вимірному просторі називається простою, якщо вона приймає лише скінчену кількість різних значень (ці значення вважаються скінченими).

Легко зрозуміти, що будь-яку просту функцію можна подати у вигляді лінійної комбінації характеристичних функцій диз’юнктної сукупності множин. І справді, якщо функція приймає значення , то покладемо , тоді:

, (1)

при цьому;

. (2)

Теорема 1.	(Вимірність простої функції)
	Проста функція , що побудована для розбиття (1) дійсної осі , вимірна тоді і тільки тоді, коли усі множини вимірні.

Необхідність. Якщо - вимірна, то кожна з множин вимірна як прообраз вимірної множини.

Достатність. Якщо усі множини вимірні, то за лемою 1 кожна з характеристичних функцій – вимірна, а тому й - вимірна лінійна комбінація вимірних функцій.

Теорема доведена.

Наслідок.	(Комбінація простих функцій)
	Лінійна комбінація та добуток простих вимірних функцій також є простими вимірними функціями.

Теорема 2.	(Границя послідовності простих функцій)
	Для будь-якої вимірної функції , що задана на вимірному просторі , існує послідовність простих вимірних функцій, що збігаються до в кожній точці . Якщо функція - обмежена на , то послідовність можна вибрати рівномірно збіжною до на . Якщо ж , то можна таким чином вибрати послідовність функцій , щоб вона була неспадною.

Доведення. Почнемо з невід’ємних функцій. Нехай , тоді покладемо:

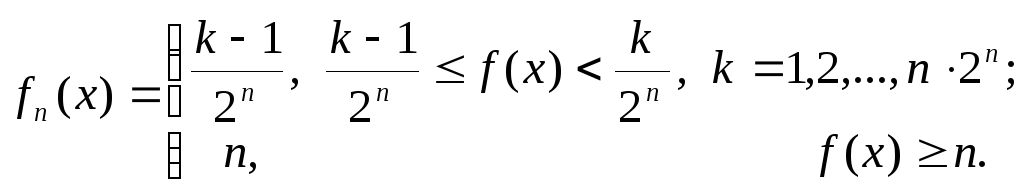(3)

Очевидно, що побудована послідовність складається з простих функцій, а також вона є неспадною. Вимірність функцій слідує безпосередньо з теореми 1. З’ясуємо її збіжність. Покажемо, що

. (4)

Якщо , то для достатньо великих будемо мати , а тому з (3) слідує, що , а тому й слідує (4) для цих значень. Якщо ж , то , що й треба було довести.

Якщо - обмежена, тобто , то при з (3) слідує: : , що й означає, що . Для невід’ємних функцій теорема доведена.

Якщо не знакостала, то розглянемо додатну та від’ємну частини функції :

, .

Оскільки - вимірні функції, то для них теорема вже доведена, а далі залишається скористатися властивістю: .

Теорема доведена.

Теорема 3.	(Лузіна про С-властивість)
	Нехай вимірна за Лебегом множина скінченої міри і нехай функція - вимірна за Лебегом, а також майже всюди скінчена. Тоді існує замкнена множина така, що звуження функції на множину є неперервною функцією, і при цьому .

Доведення. Розглянемо спочатку випадок простої вимірної функції , де простір - складений з вимірних множин. З відомих раніше тверджень існує замкнена множина : 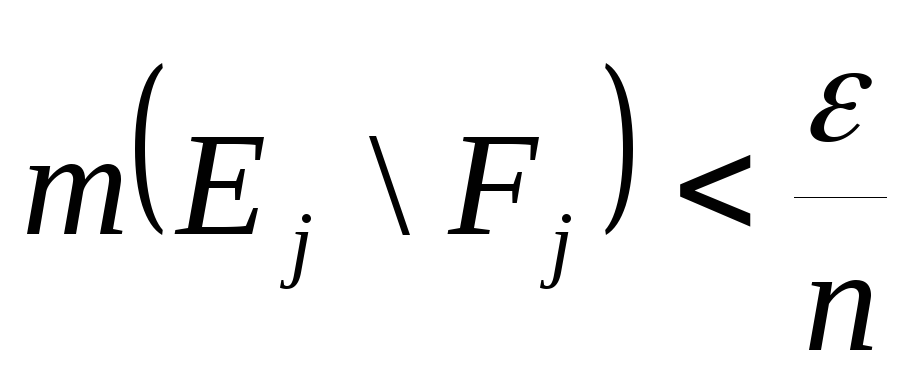, а також покладемо . За побудовою - замкнена, крім того , а також 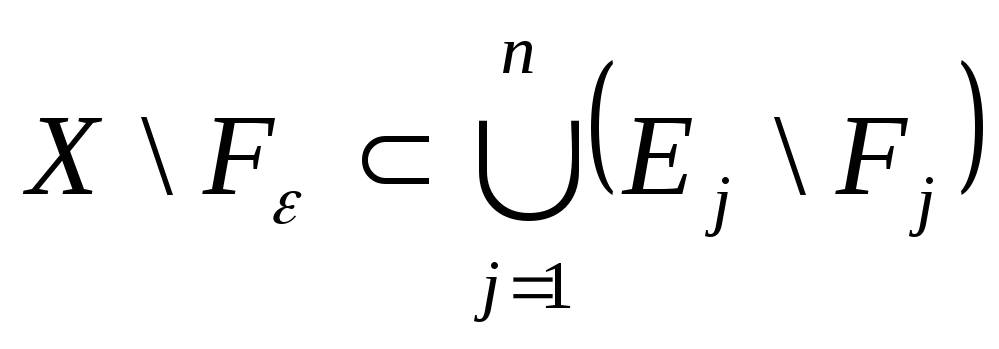, а тому . Крім того, звуження на - неперервне.

Нехай тепер - довільна вимірна функція. Побудуємо послідовність простих функцій , що збігається до на . З теореми Єгорова існує така вимірна множина : 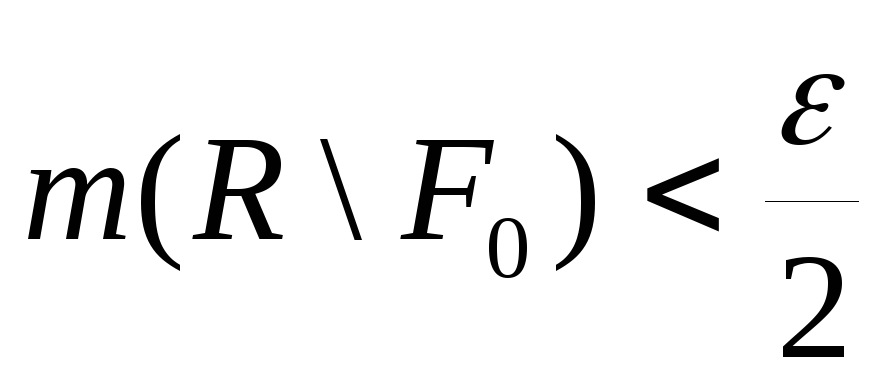та на множині . Легко зрозуміти, що можна вважати множину замкненою. З першої частини теореми існує замкнена множина така, що , та звуження на множину - неперервне. Покладемо . З умови неперервності на та рівномірної збіжності слідує, що й гранична функція неперервна. Крім того .

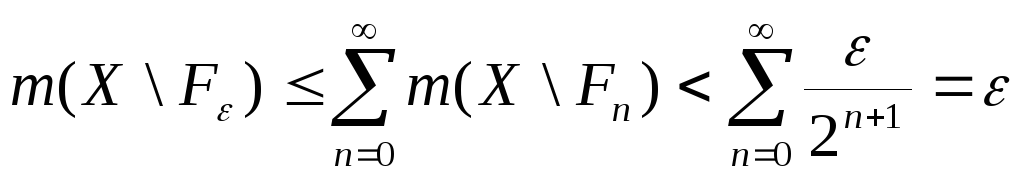Теорема доведена.