
- •Семінар №3 Киів2013Робота з об’єктами, таблицями, формулами
- •4. Статистичні властивості оцінок методу найменших квадратів. Теорема Гауса-Маркова
- •5. Розклад дисперсії залежної змінної. Коефіцієнт детермінації. Скоригований коефіцієнт детермінації
- •6. Перевірка статистичних гіпотез у моделі множинної лінійної регресії
- •6.1. Перевірка адекватності регресії
- •Динаміка чисельності працюючих та кількості оргтехніки за останні 6 місяців
- •24.02.2017
- •24.02.2017
- •24.02.2017
- •Список літератури
Шпак
Е.В.
Семінар №3 Киів2013Робота з об’єктами, таблицями, формулами
ЕВК-56-90
К71
Затверджено кафедрою економічної кібернетики Київського національного університету імені Т. Шевченка.
Брошура студентки 2 курсу спеціальності «економічна кібернетика». Дана брошура містить лабораторну роботу. Робота складається з послідовного виконання завдань семінару, запропонованих до розгляду Ставицьким Андрієм Володимировичем.
The brochure was compiled by second-year student in “Economic cybernetics”. This brochure contains laboratory work. The work consists of sequential tasks of seminar that offered for consideration by Stavytskyy Andriy Volodymyrovych.
Шпак Е.В.
Системи обробки економічної інформації. Семінар №3. Видавництво – Освіта, 2013 – ст15.
ISBU 156-3466-4345
Зміст
Динаміка чисельності працівників та кількості оргтехниіки 12
Структурна схема Національної системи масових електронних платежів (НСМЕП) 14
Структурна схема 15
Черняк, О. С. (2001). Теорія ймовірностей та математична статистика. Київ: Знання. 16
Список літератури 17
Нехай розглядається множинна регресія виду:
 .1
.1
Використовуючи введені вище векторно-матричні позначення, можна записати
 .
.
Вектор
залишків методу найменших квадратів
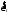 визначається як
визначається як
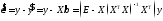 .
.
Зміст поняття залишків такий же, як і в моделі простої лінійної регресії. Запишемо систему нормальних рівнянь у такому вигляді:
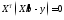 ,
,
або
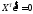 .
11\* MERGEFORMAT ()
.
11\* MERGEFORMAT ()
Очевидно,
що вектор залишків ортогональної до
кожного стовпчика матриці Х. згадаємо,
що
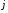 -й стовпчик цієї матриці утворюють
значення
-й стовпчик цієї матриці утворюють
значення -го регресора. Таким чином,залишки
методу найменших квадратів ортогональні
до регресорів.
Якщо розглядається модель з константою,
то першій стовпчик матриці Х складається
з одиниць, і з рівняння 12випливає, що
-го регресора. Таким чином,залишки
методу найменших квадратів ортогональні
до регресорів.
Якщо розглядається модель з константою,
то першій стовпчик матриці Х складається
з одиниць, і з рівняння 12випливає, що
 . 22\* MERGEFORMAT ()
. 22\* MERGEFORMAT ()
З останньої рівності випливає, що в моделі з константою сума залишків методу найменших квадратів дорівнює нулю.
Оскільки
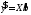 ,
то
,
то
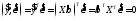 33\* MERGEFORMAT ()
33\* MERGEFORMAT ()
внаслідок
2. \* MERGEFORMAT Крім того вектор
 є лінійною комбінацією стовпчика матриці
є лінійною комбінацією стовпчика матриці ,
тобто регресорів.
,
тобто регресорів.
Зі співвідношення 3 випливає важливий наслідок: регресійна гіперплощина в моделі з константою проходить через точку, координати якої дорівнюють середнім значення незалежних змінних.
4. Статистичні властивості оцінок методу найменших квадратів. Теорема Гауса-Маркова
Покажемо,
що МНК-оцінка є незміщеною оцінкою
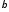 :
:
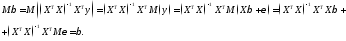
Знайдемо коваріаційну матрицю МНК-оцінки:

Таким чином,
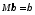
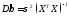 .
44\* MERGEFORMAT ()
.
44\* MERGEFORMAT ()
Безпосередньо
дисперсії кожного з коефіцієнтів
регресії знаходяться на головній
діагоналі отриманої матриці. Проте
наведені формули не можна використовувати
для перевірки гіпотез та інтервального
оцінювання, оскільки до них входить
невідомий параметр – дисперсія збурень
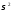 .
Можна показати, що статистика
.
Можна показати, що статистика
 ,
55\* MERGEFORMAT ()
,
55\* MERGEFORMAT ()
де
 - кількість регресорів, включаючи
константу, є незміщеною оцінкою
- кількість регресорів, включаючи
константу, є незміщеною оцінкою .
Якщо збурення нормально розподілені,
то
.
Якщо збурення нормально розподілені,
то має багатовимірний нормальний розподіл,
математичне сподівання і дисперсія
якого обчислюється за формулою 4.
має багатовимірний нормальний розподіл,
математичне сподівання і дисперсія
якого обчислюється за формулою 4.
Величина

має
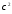 -
розподіл з
-
розподіл з ступенями свободи і не залежать від
ступенями свободи і не залежать від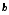 .
Оцінка коваріаційної матриці коефіцієнтів
регресії за методом найменших квадратів
одержується підстановкою до формули
4 виразу 5 замість дисперсії збурень
.
Оцінка коваріаційної матриці коефіцієнтів
регресії за методом найменших квадратів
одержується підстановкою до формули
4 виразу 5 замість дисперсії збурень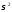 :
:
 .
.
Позначимо
через
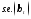 оцінку середньоквадратичного відхилення
коефіцієнта
оцінку середньоквадратичного відхилення
коефіцієнта .
Розмірковуючи так, як у випадку простої
регресії, приходимо до висновку, що
.
Розмірковуючи так, як у випадку простої
регресії, приходимо до висновку, що
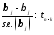 ,
,
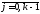 .
66\* MERGEFORMAT ()
.
66\* MERGEFORMAT ()
Оцінки
методу найменших квадратів є лінійними
у тому розумінні, що
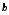 є лінійною функцією
є лінійною функцією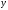 .
Наступна теорема встановлює оптимальні
властивості оцінки методу найменших
квадратів
.
Наступна теорема встановлює оптимальні
властивості оцінки методу найменших
квадратів
Теорема Гауса-Маркова. 1. Нехай припущення про нормальність збурень не накладається. Тоді МНК-оцінки мають мінімальну коваріаційну матрицю в класі незміщених лінійних оцінок.
2. Припустимо, що збурення мають нормальних розподіл. МНК-оцінки мають мінімальну коваріаційну матрицю в класі усіх незміщених оцінок.
Таким
чином, оцінки коефіцієнтів
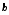 мають найменші дисперсії серед оцінок
відповідних класів.
мають найменші дисперсії серед оцінок
відповідних класів.
