Лекции по математике и информатике / Лекция 17 - Теория множеств

Лекция 17

Тема: Алгебра логики. Теория множеств.

Время: 2 ч.

Вопросы:

1. Алгебра логики.

2. Основные законы преобразований алгебры логики.

3. Понятие множества.

4. Множества.

5. Операции над множествами.

6. Обозначения некоторых числовых множеств.

7. Счетные и несчетные множества.

8. Координатная прямая.

1. Алгебра логики.

Алгебра логики возникла в середине XIX века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные задачи алгебраическими методами.

Алгебра логики - раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.

Логическое высказывание - любое повествовательное предложение, в отношении которого однозначно можно сказать, истинно оно или ложно.

Пример 1:

Предложение «6 - четное число» является высказыванием, т.к. оно истинное.

Существуют предложения, в которых для выяснения истинности или ложности требуются дополнительные сведения. Такие предложения являются высказывательными формами.

Высказывательная форма - повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями.

Пример 2:

Предложение «площадь поверхности Индийского океана равна 75 млн.км²» - и истинно (значение приближенное, приемлемо на практике) и ложно (указанное значение неточное).

Из логических высказываний составляются логические формулы.

Например, X Y = X ٧Y

2. Основные законы алгебры логики.

В алгебре логики выполняются следующие основные законы, позволяющие производить тождественные преобразования логических выражений:

Закон	для ИЛИ (+)	для И (*)
1. Переместительный	X ٧ Y = Y ٧ X	X * Y = Y * X
2. Сочетательный	X ٧ (Y ٧ Z) = (X ٧ Y) ٧ Z	X * (Y * Z) = ( X * Y) * Z
3. Распределительный	X * (Y ٧ Z) = X * Y ٧ X * Z	X ٧ Y *Z = (X ٧ Y) * (X ٧ Z)
4. Правила де Моргана	X ٧ Y = X * Y	X * Y = X ٧ Y
5. Идемпотенция	X ٧ X = X	X * X = X
6. Поглощения	X ٧ X * Y = X	X * (X ٧ Y) = X
7. Склеивания	(X * Y) ٧ (X * Y) = Y	(X ٧ Y) * (X ٧ Y) = Y
8. Операция переменной с ее инверсией	X ٧ X = 1	X * X = 0
9. Операция с константами	X ٧ 0 = X X ٧ 1 = 1	X * 0 = 0 X * 1 = X
10. Двойного отрицания	X = X

3. Понятие множества

В современной математике понятие множества является одним из основных. Универсальность этого понятия в том, что под него можно подвести любую совокупность явлений, предметов и объектов реального мира. Сами множества так же могут объединяться во множества. Например, математики говорят о множестве фигур на плоскости, о множестве тел в пространстве, но каждую фигуру, каждое тело они мыслят как множество точек.

Плодотворность теоретико-множественной концепции в том, что она породила весьма богатый и мощный арсенал широких понятий и универсальных методов.

4. Множества

Наиболее простая структура данных, используемая в математике, имеет место в случае, когда между отдельными изолированными данными отсутствуют какие-либо взаимосвязи. Совокупность таких данных представляет собой множество.

Понятие множества является неопределяемым понятием. Множество не обладает внутренней структурой. Множество можно представить себе как совокупность элементов, обладающих некоторым общим свойством.

Для того чтобы некоторую совокупность элементов можно было назвать множеством, необходимо, чтобы выполнялись следующие условия:

• Должно существовать правило, позволяющее определить, принадлежит ли указанный элемент данной совокупности.

• Должно существовать правило, позволяющее отличать элементы друг от друга. (Это, в частности, означает, что множество не может содержать двух одинаковых элементов).

Множества обычно обозначаются заглавными латинскими буквами. Если элемент принадлежит множеству , то это обозначается:

Если каждый элемент множества является также и элементом множества , то говорят, что множество является подмножеством множества :

Подмножество множества называется собственным подмножеством, если В  А. Используя понятие множества можно построить более сложные и содержательные объекты.

5. Операции над множествами.

Суть понятия «множество» вполне передается словами: «совокупность», «собрание», «набор» и т.д. Однако, как абстрактное математическое понятие множество неопределимо.

Определить любое конкретное множество - значит, определить какие предметы (явления, объекты) принадлежат данному множеству, а какие не принадлежат. Иначе говоря, всякое множество однозначно определяется своими элементами.

Для обозначения принадлежности элемента некоторому множеству используется знак .

А для обозначения не принадлежности используется знак .

Пример 3:

• Яблоки 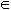ФРУКТЫ, где ФРУКТЫ = {груши, апельсины, яблоки, виноград…};

• 5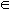А = {1,2,3,4,5,6,7};

• n N (читается: n принадлежит множеству натуральных чисел N).

Основными операциями над множествами являются объединение, пересечение и разность.

Объединением двух множеств называется новое множество

Пересечением двух множеств называется новое множество

Разностью двух множеств называется новое множество

Если класс объектов, на которых определяются различные множества обозначить (Универсум), то дополнением множества называют разность

6. Обозначения некоторых числовых множеств

N ― множество натуральных чисел.

Z ― множество целых чисел.

Q ― множество рациональных чисел.

R ― множество действительных чисел.

Одной из основных характеристик любого множества является его мощность. Под мощностью множества принято понимать число его элементов.

Пример 4:

1. |А| = 5, где А = {стул, стол, кресло, диван, секретер}.

2. |С| = 2, где С = {3,88).

Могут существовать множества, число элементов которых бесконечно. Кроме того, можно говорить о счетных и несчетных множествах.

Принято также вводить понятие пустого множества, т.е. множества, на содержащего ни одного элемента. Обозначение пустого множества O.

Если множества равны по мощности, т.е. имеют одинаковое число элементов, то их можно сравнивать по отношению равенства. При этом два множества равны, если они равны по мощности и все элементы одного множества совпадают с элементами другого. Обозначается: А = В или B = A. Соответственно можно говорить, что некоторые множества не равны, если они различаются хотя бы одним элементом. (А ≠ В). Кроме того множества могут находиться и в некоторых других отношениях друг с другом.

7. Счетные и несчетные множества

Пусть, например, А и В ― некоторые множества. Тогда их возможные взаимоотношения можно рассмотреть в виде таблицы:

Диаграмма Венна

Диаграмма Венна

Диаграмма Венна

Д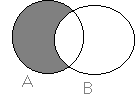иаграмма Венна

Исходя из вышеизложенного, запишем некоторые свойства множеств:

1. А \ А = 0

2. А \ 0 = А

3. АА = А, АА = А

4. АВ = ВА, АВ = В А

8. Координатная прямая

Проведем прямую и отметим на ней точку О, которую примем за начало отсчета. Выберем направление и единичный отрезок. Говорят, что задана координатная прямая. Каждому натуральному числу соответствует одна единственная точка на координатной прямой.

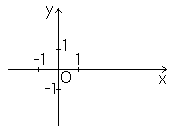
Модуль числа ― это расстояние от начала отсчета до точки, соответствующей данному числу.

Выводы по теме:

1. Суть понятия «множество» вполне передается словами: совокупность, собрание, набор и т.д. Однако, как абстрактное математическое понятие множество неопределимо.

2. Обозначения некоторых числовых множеств.

3. Под мощностью множества принято понимать число его элементов.

4. Пустое множество ― это множество, на содержащего ни одного элемента. Обозначение пустого множества 0.

5. Два множества равны, если они равны по мощности и все элементы одного множества совпадают с элементами другого. Обозначается: А = В или B = A.

6. Проведем прямую и отметим на ней точку О, которую примем за начало отсчета. Выберем направление и единичный отрезок. Говорят, что задана координатная прямая.

7. Модуль числа ― это расстояние от начала отсчета до точки, соответствующей данному числу.

5