X 1 1

X2 Y

X3

_____

Ответ: y = (x1 or x2) or x3

Задание

Практическая работа № 3

Тема: Логические основы ПК. Алгебра логики. Простейшие логические элементы

И, ИЛИ, НЕ, логические операции конъюнкция, дизъюнкция и инверсия.

Таблица истинности.

Время: 2 ч.

Цель: первичное получение навыков построения логических схем.

Перечень оборудования: курс лекций, таблица схем простейших логических элементов.

Задания

1. Составить логические схемы следующих функций:

1. y = (x1 & x2) & x1

__ __

2. y = (x1 or x2) & x3

_________ _______

3. y = (x1 & x2) or x3

___ _ __ __

4. y = (x1 or x2) & x1

5. y = (x1 or x2) or (x3 & x4).

6. y= (x1 or x2) & x3

7. Y = (x1 or x2) or (x3 and x4).

____ _____

8. Y = (x1 or x2) & x3

9. Y = (x1 & x2) & (x1 or x2)

2. По данным логическим схемам записать операторы и таблицы истинности.

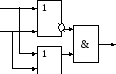х1

a) b) c)

x1 х2 х1 У

x2 Y У х2

x3

Практическая работа № 4

Тема: Законы алгебры логики.

Время: 2 ч.

Цель: первичное получение навыков построения логических схем.

Перечень оборудования: курс лекций, таблица схем простейших логических элементов.

Задания

1. Преобразовать оператор, используя основные законы алгебры логики, построить схемы и таблицу истинности:

1. Y = (x1 & x2) or (x3 & x4)

2. Y = (x1 & x2) or (x3 or x4)

3. Y = (x1 or x2) & x1

4. Y = x1 & (x2 or x3)

5. Y= x1 & x2

6. Y= (x1 or x2 )or (x1 & x2)

__

7. Y = (x1 or x2 or x3)

2. По данным логическим схемам записать операторы и таблицы

истинности.

d) е)

x1 х1

x2 х2

Y х3 у

x3

x4

f) g)

x1 х1

x2 х2

Y У

x3 х3

6