Правила дерева вывода

Уровень дерева	Номер правила	Содержание правила	Коэффициент определенности
1	1	Если С1 ИЛИ С2 ИЛИ Е12, ТО Г	0,8
2	2	ЕСЛИ С3 И С4, ТО С1	0,7
2	3	ЕСЛИ Е8 ИЛИ Е9 ИЛИ Е11, ТО С2	0,8

Таблица 8.7.

Расшифровка обозначений в дереве вывода

Обозначение узла	Содержание узла в дереве вывода	Коэффициент определенности
Г	Акции покупать	?
С1	В текущем году прибыль предприятия не снижалась	?
С2	Риск потерь средств низкий	?
С3	Выручка в текущем году не снижалась	0,4
С4	Затраты не возросли	0,6
Е8	Репутация предприятия высокая	0,7
Е9	Отдача от вложений больше уровня инфляции	0,4
Е11	Цена акций допустимая	0,3
Е12	Стоимость акционерного капитала на акцию не меньше ее цены	0,5

Рассчитаем коэффициент определенности для гипотезы Г.

В дереве вывода имеется два правила с союзом ИЛИ и одно правило с союзом И. Коэффициенты определенности для заключений С1, С2 и Г равны:

ct(С1) = 0,4*0,7 = 0,28;

ct (C2) = 0,7*0,8 = 0,56;

ct (Г) = 0,56*0,8 = 0,45.

Таким образом, коэффициент определенности гипотезы "Акции данного предприятия являются перспективными" довольно низкий, так как равен лишь 0,45 в диапазоне от 0 до 1.

Современные экспертные системы, используемые для формирования решений, в большинстве случаев базируются на базах знаний. Как правило, в основе такого рода систем лежат различные деревья выводов.

74. Формирование решений в условиях риска.

В условиях риска можно использовать деревья решений, если альтернативы, отражающие варианты решения, находятся в отношениях соподчиненности.

Как правило, условия появления альтернатив носят качественный характер и определяются вероятными величинами.

Иерархические отношения удобно представлять в виде дерева: дуги дерева отражают альтернативы частичных решений, а узлы – результаты.

Таким образом, получают дерево решений, с помощью которого можно представлять вероятностные (частотные) характеристики условий.

Это позволяет достаточно просто определять результат принятия решения на том или ином уровне дерева с помощью математического ожидания:

где Е(общего_результата) – математическое ожидание общего или промежуточного результата;

p_i – вероятность наступления i-го события;;

d_i – результат (частный), получаемый при наступлении i-го события;

n – количество событий, влияющих на общий (промежуточный) результат.

Пример смотри у Одинцова Б.Е.

75. Формирование решений с помощью нейросетей.

Нейросетевые технологии, в отличие от экспертных систем, предназначены для воспроизведения неосознанных мыслительных усилий человека (например, человек плохо знает, как он узнает цвет предмета).

Такого рода технологии используются для распознавания каких-либо событий или предметов.

С их помощью можно воспроизвести многочисленные связи между множеством объектов.

Принципиальное отличие искусственных нейросетей от обычных программных систем, например экспертных, состоит в том, что они не требуют программирования. Они сами настраиваются, т. е. обучаются тому, что требуется пользователю.

Известны следующие основные сферы применения нейросетей:

1. Экономика и бизнес: предсказание поведения рынков, предсказание банкротств, оценка стоимости недвижимости, автоматическое рейтингование, оценка кредитоспособности, прогнозирование курса валют.

2. Медицина: обработка медицинских изображений, диагностика.

3. Интернет: ассоциативный поиск информации.

4. Автоматизация производства: оптимизация режимов производственного процесса, диагностика качества продукции, предупреждение аварийной ситуации.

5. Политические технологии: обобщение социологических опросов.

6. Безопасность и охранные системы: системы идентификации личности, распознавание автомобильных номеров, распознавание аэрокосмических снимков.

7. Геологоразведка: анализ сейсмических данных, оценка ресурсов месторождений.

Искусственные нейросети состоят из искусственных нейронов

Искусственный нейрон представляет собой математическую модель естественного нейрона, имеющего несколько входов (вектор входных сигналов) и один выход.

Этот выход направлен либо к другому нейрону, либо к выходу из нейронной системы.

Вектор входных сигналов преобразуется нейроном в выходной сигнал с использование сумматора и специального нелинейного преобразователя.

Каждый из нейронов на рис. 8.12 осуществляет следующие операции:

,

где -выходной сигнал j-го нейрона, характеризуемый значением в некотором диапазоне;

f()- функция возбуждения нейрона, преобразующая выходной сигнал, в форму, воспринимаемую другим нейроном;

w_i,j - весовой коэффициент связи между i-м и j-м нейронами;

x_i.j - логическая переменная, принимающая значение 1, если связь между i-м и j-м нейронами возбуждена и 0 – в противном случае;

- пороговое значение функции возбуждения.

Один нейрон работает следующим образом:

• на его вход поступает набор входных сигналов;

• нейрон суммирует (учитывает) входные сигналы и генерирует либо не генерирует выходной сигнал, который направляется либо в другие нейроны, либо на выход сети.

Связь между нейронами характеризуется интенсивностью (силой возбуждения), называемой также синаптическим весом. Представить их можно в виде синаптической матрицы, элементы которой указывают на силу возбуждения связей между нейронами (подробнее см. [19]).

Применение нейросетей предполагает выполнение следующих этапов:

1. Постановка задачи: формирование цели применения нейросети (например, прогнозирование курса ценных бумаг).

2. Обучение нейросети: подготовка обучающих примеров, которые представляют собой уже известные результаты решения задачи без нейросети и предъявление их ей.

3. Эксплуатация сети: сети предъявляется некоторая ситуация, которая либо распознается, либо нет.

Обучение нейронных сетей представляют собой последовательный процесс изменения синаптических весов, отражающих силу связей между нейронами. Известно два вида обучения: с учителем и без такового.

Рассмотрим первый случай.

Предполагаются, что некоторая величина , зависит от ряда характеристик .

Необходимо обучить нейросеть распознаванию некоторого значения при определенных значениях характеристик .

Готовится набор обучающих примеров, которые состоят из набора исходных векторов и соответствующих им выходных значений.

Если, например, - будущая цена акций через три дня, а -сегодняшние котировки некоторого набора акций, то каждый обучающий пример представляет собой котировки акций на некоторую прошлую дату плюс стоимость акций () через три дня после этой даты (котировка – это определение рыночного курса ценной бумаги).

Эти примеры подаются на вход сети.

Вначале на вход подается первая строка.

Нейросеть формирует начальную зависимость между y₁ и _.

На основе этой зависимости вычисляется текущее значение _, которое сравнивается с эталонным значением .

Если разница превышает допустимый уровень, то алгоритм обучения изменяет синаптические веса (весовые коэффициенты), после чего эта строка вновь подается на вход сети для обучения до тех пор, пока результат не будет удовлетворительным.

Затем подается следующая строка _… и _.

Процесс повторяется до тех пор, пока суммарная ошибка в реакции сети на все строки не станет меньше заданной.

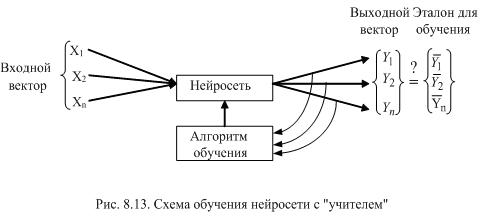
Схема обучения с "учителем" представлена на рис. 8.13.