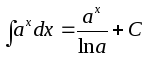Неопределенные интегралы
1. Понятие неопределенного интеграла
Интегрирование
– операция,
обратная дифференцированию, которая
позволяет определять функцию
![]() ,
для которой заданная функция
,
для которой заданная функция
![]() является ее производной:
является ее производной:
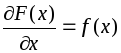 .
.
Другими словами, если операция дифференцирования состоит в нахождении производной, то интегрирование – это операция отыскания первообразной.
Функция
![]() называется первообразной для функции
называется первообразной для функции
![]() ,
на промежутке
,
на промежутке
![]() ,
если для каждой точки этого промежутка
,
если для каждой точки этого промежутка
![]() .
.
Теорема.
Если
![]() и
и
![]() – любые две первообразные для данной
функции
– любые две первообразные для данной
функции
![]() на промежутке
на промежутке
![]() ,
то для всех
,
то для всех
![]() выполняется равенство
выполняется равенство
![]() .
.
Доказательство:
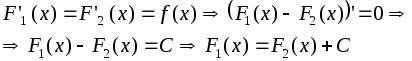
Таким
образом, все семейство первообразных
для данной функции
![]() имеет вид
имеет вид
![]() ,
где
,
где
![]() одна из первообразных, а
одна из первообразных, а
![]() произвольная постоянная.
произвольная постоянная.
Совокупность
всех первообразных для функции
![]() на промежутке
на промежутке
![]() называется неопределенным интегралом
функции
называется неопределенным интегралом
функции
![]() .
.
Неопределенный интеграл обозначается следующим образом:
![]() ,
,
где
![]() знак интеграла;
знак интеграла;
![]() подынтегральная
функция;
подынтегральная
функция;
![]() подынтегральное
выражение.
подынтегральное
выражение.
В определении неопределенного интеграла не исключается возможность того, что подынтегральная функция является сложной, однако при проверке правильности нахождения первообразной это несущественно, поскольку дифференцировать следует лишь по переменной, стоящей под знаком дифференциала.
Можно
показать, что достаточным
условием интегрируемости функции
![]() на промежутке
на промежутке
![]() является ее
непрерывность, в то время как для ее
дифференцируемости непрерывность
является лишь необходимым условием, но
не достаточным.
является ее
непрерывность, в то время как для ее
дифференцируемости непрерывность
является лишь необходимым условием, но
не достаточным.
2. Свойства неопределенного интеграла
-
Производная неопределенного интеграла равна подынтегральной функцией:
![]()
![]()
Эти свойства означают, что интегрирование и дифференцирование – взаимно обратные операции.
-
Если
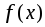 и
и
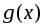 – интегрируемые функции, т.е. на
промежутке
– интегрируемые функции, т.е. на
промежутке
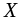 они имеют первообразные, то сумма
функций
они имеют первообразные, то сумма
функций
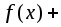
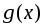 также интегрируема и
также интегрируема и
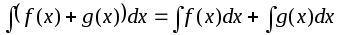 .
. -
Если
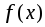 – интегрируемая функция, а
– интегрируемая функция, а
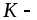 постоянная величина, то
постоянная величина, то
 – также интегрируемая функция и
– также интегрируемая функция и
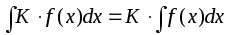 .
.
Таким образом, свойства 3 и 4 указывают на линейность операции интегрирования:
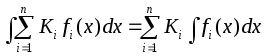 ,
,
где
![]() постоянные;
постоянные;
![]() интегрируемые
функции.
интегрируемые
функции.
-
Если
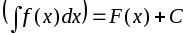 ,
а также
,
а также
 дифференцируемая функция, то
дифференцируемая функция, то
![]() .
.
Простым обращением известных формул дифференцирования элементарных функций получается таблица простейших неопределенных интегралов.
|
|
|
|
|
|
|
|
|
|
Чтобы найти неопределенный интеграл от какой-либо функции, достаточно свести его к одному или нескольким табличным интегралам из вышеприведенной таблицы.
Интеграл функция рационализация
3. Замена переменных
Для
упрощения подынтегральной функции и,
тем самым, для нахождения интеграла
![]() часто применяется так называемая
подстановка или замена переменных.
часто применяется так называемая
подстановка или замена переменных.
Если
обозначить
![]() и сделать соответствующие преобразования
в заданном подынтегральном выражении,
полученный интеграл при удачном выборе
функции
и сделать соответствующие преобразования
в заданном подынтегральном выражении,
полученный интеграл при удачном выборе
функции
![]() может оказаться более простым или даже
табличным.
может оказаться более простым или даже
табличным.
Для некоторых типов подынтегральных функций известны такие подстановки, которые приводят к цели. Ниже будут рассматриваться многие из них.
Например:
-
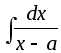 .
Если применить замену
.
Если применить замену
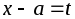 ;
;
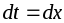 ,
то получим:
,
то получим:
![]() .
.
-
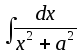 .
Применим замену
.
Применим замену
 ;
;
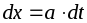 .
В результате получим:
.
В результате получим:
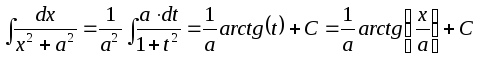 .
.
-
 Как и в предыдущем
случае, применим замену
Как и в предыдущем
случае, применим замену
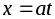 ;
;
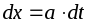 .
В результате получим:
.
В результате получим:
![]() .
.
-
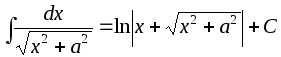 .
.
Интегрирование этого выражения будет проведено позднее при подробном рассмотрении метода замены переменных.
Наряду с заменой переменных часто применяется метод разложения, который опирается на линейные свойства интегралов. Это можно проиллюстрировать следующим примером:
![]()
4. Интегрирование по частям
Если
функции
![]() и
и
![]() дифференцируемы на множестве
дифференцируемы на множестве
![]() и, кроме того, на этом множестве существует
интеграл
и, кроме того, на этом множестве существует
интеграл
![]() ,
то на нем существует и интеграл
,
то на нем существует и интеграл
![]() ,
причем
,
причем
![]() .
Действительно,
если проинтегрировать формулу нахождения
дифференциала произведения двух функций:
.
Действительно,
если проинтегрировать формулу нахождения
дифференциала произведения двух функций:
![]() ,
,
то можно получить следующее соотношение между первообразными от этих функций:
![]() .
.
Такой
способ нахождения интеграла называется
интегрированием
по частям. Этот
способ целесообразно применять, если
интеграл, стоящий в правой части проще
исходного. При использовании метода
интегрирования по частям задана левая
часть равенства, т.е. функция
![]() и дифференциал
и дифференциал
![]() .
Таким образом, выбор функций
.
Таким образом, выбор функций
![]() и
и
![]() неоднозначен, причем не каждый способ
выбора этих функций ведет к упрощению
первоначального интеграла. Функции,
интегрируемые по частям, можно схематично
разделить на три группы.
неоднозначен, причем не каждый способ
выбора этих функций ведет к упрощению
первоначального интеграла. Функции,
интегрируемые по частям, можно схематично
разделить на три группы.
1.
Интегралы, подынтегральная функция
которых содержит в качестве множителя
одну из следующих функций:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
при условии, что оставшаяся часть
подынтегральной функции представляет
собой производную известной функции.
,
при условии, что оставшаяся часть
подынтегральной функции представляет
собой производную известной функции.

В
случае если подынтегральная функция
содержит в качестве множителя одну из
перечисленных выше функций в степени
![]() ,
то операцию интегрирования по частям
придется повторять
,
то операцию интегрирования по частям
придется повторять
![]() раз.
раз.
2.
Интегралы, подынтегральная функция
которых содержит в качестве множителя
одну из следующих функций:
![]() ,
,
![]() ,
,
![]() ,
a
также, полином
,
a
также, полином
![]() й
степени
й
степени
![]() :
:
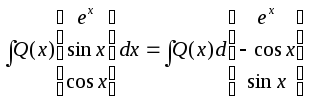 .
.
Для
вычисления интегралов второй группы
нужно формулу интегрирования по частям
применять
![]() раз, причем в качестве функции
раз, причем в качестве функции
![]() нужно брать многочлен соответствующей
степени. После каждого интегрирования
степень полинома будет понижаться на
единицу.
нужно брать многочлен соответствующей
степени. После каждого интегрирования
степень полинома будет понижаться на
единицу.
3. Интегралы вида:
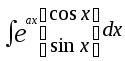 ;
;
![]() ;
;
![]() .
.
Применение формулы интегрирования по частям может привести к ситуации, когда интеграл в правой части и интеграл в левой части равенства совпадают, т.е. получается равенство вида:
![]() ,
,
где
![]() исходный интеграл;
исходный интеграл;
![]() постоянная
постоянная
![]() .
.
В
этом случае применение метода
интегрирования по частям позволяет
получить уравнение первого порядка для
![]() ,
из решения которого находится исходный
интеграл
,
из решения которого находится исходный
интеграл
![]() :
:
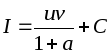 .
.
Причем,
метод интегрирования по частям может
применяться многократно и любой из
сомножителей можно всякий раз принимать
за
![]() .
.
Большое количество интегралов, не входящих в эти три группы, у которых невозможно выделить общий признак для группировки, также вычисляются методом интегрирования по частям. К таким интегралам можно отнести:
![]() ,
,
![]() ,
,
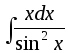 ,
,
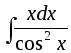 ,
,
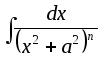

 ;
; ;
;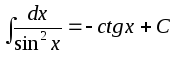 ;
;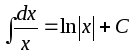 ;
; ;
;