10. Несобственные интегралы

При рассмотрении задачи интегрирования непрерывных и кусочно-непрерывных функций предполагалось, что эти подынтегральные функции являются ограниченными на отрезке интегрирования , а сам отрезок является конечным. Постановка задачи интегрирования возможна, когда одно из этих условий или оба они нарушены. В этом случае интегралы называются несобственными, а задача интегрирования формулируется несколько иначе. Рассмотрим оба случая:

• Подынтегральная функция неограниченна;

• Промежуток интегрирования бесконечен.

11. Интегрирование неограниченных функций

Предположим, что функция определена и непрерывна на промежуткеи стремится к бесконечности при. Точкуназываютособой, если функция не ограничена в любой окрестности этой точки, но ограничена на любом отрезке, заключенном в промежутке.

Определение: Пусть функция неограничена на отрезке, однако ограничена на любом меньшем отрезке, где. Тогда, если существует конечный предел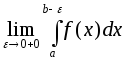, то его принимают за несобственный интегралот неограниченной функции, т.е.:

,

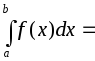
а интеграл называется сходящимся. Если этого предела не существует, или он бесконечен, то интеграл называется расходящимся.

Если особой точкой является точка , то несобственный интеграл определяется аналогично:

.

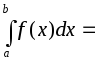
Если единственной особой точкой является внутренняя точка , принадлежащая интервалу, то полагают, что:

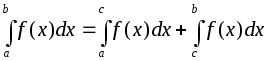
при условии, что оба несобственных интеграла справа сходятся.

12. Интегрирование по бесконечному промежутку

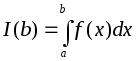Определение: Пусть функция интегрируема на каждом отрезке, т.е. существует определенный интеграл. Тогда за несобственный интеграл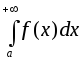принимают предел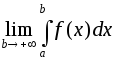. Если этот предел существует и конечен, то интеграл называется сходящимся. Если этого предела не существует, или он бесконечен, то интеграл называется расходящимся.

Аналогично можно определить несобственный интеграл с бесконечным нижним пределом:

.

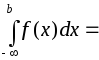
При рассмотрении интеграла с бесконечными верхним и нижним пределами 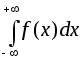выбирается произвольная промежуточная точкаи используется свойство аддитивности:

.

Если оба несобственных интеграла справа сходятся, то говорят, что существует и несобственный интеграл . Нетрудно показать, что выбор точкине влияет на конечный результат.

Следует отметить важное свойство несобственных интегралов, отличающее их от определенных интегралов.

Известно, что для определенных интегралов справедливо утверждение: если существует 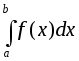, то существует и интеграл.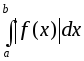

В случае несобственных интегралов имеет место следующее утверждение: из сходимости несобственного интеграла от следует сходимость несобственного интеграла от. В этом случае говорят об абсолютной сходимости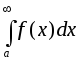. В то же время, сходимость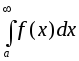не означает сходимости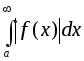. В этом случае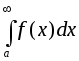называется условно сходящимся.

13. Приближенное вычисление определенных интегралов

Задача вычисления определенного интеграла не всегда может быть сведена к первообразной, поэтому разработаны численные методы, которые позволяют найти значение интеграла с достаточно высокой точностью. Суть этих методов – в замене подынтегральной функции интерполяционным многочленом. При этом возникает альтернативный выбор: осуществить замену подынтегральной функции одним интерполяционным многочленом высокой степени, описывающим изменение функции на всем интервале интегрирования .