
- •Определенные интегралы
- •1. Интегральные суммы
- •3. Равномерно непрерывные функции
- •4. Интегрируемость непрерывных, разрывных и монотонных функций
- •6. Оценки интегралов. Формулы среднего значения
- •7. Основные правила интегрирования
- •8. Приложения определенного интеграла. Площадь плоской фигуры
- •9. Объемы тел вращения
- •10. Несобственные интегралы
- •11. Интегрирование неограниченных функций
- •12. Интегрирование по бесконечному промежутку
- •13. Приближенное вычисление определенных интегралов
- •14. Формула прямоугольников
- •15. Формула трапеций
3. Равномерно непрерывные функции
Определение:
Функция
![]() называетсяравномерно
непрерывной на множестве
называетсяравномерно
непрерывной на множестве
![]() ,
если для любого числа
,
если для любого числа![]() можно указать такое
можно указать такое![]() ,
что для любых двух точек
,
что для любых двух точек![]() и
и![]() множества
множества![]() ,
удовлетворяющих уравнению
,
удовлетворяющих уравнению![]() ,
выполняется неравенство
,
выполняется неравенство![]() .
.
Теорема
(теорема Кантора
о равномерной непрерывности):
Функция
![]() ,
определенная и непрерывная на сегменте
,
определенная и непрерывная на сегменте![]() равномерно непрерывна на этом сегменте.Следствие:
Пусть функция
равномерно непрерывна на этом сегменте.Следствие:
Пусть функция
![]() непрерывна на сегменте
непрерывна на сегменте![]() .
Тогда для любого числа
.
Тогда для любого числа![]() можно указать такое
можно указать такое![]() ,
что на каждом принадлежащем сегменту
,
что на каждом принадлежащем сегменту![]() частичном сегменте
частичном сегменте![]() ,
длина
,
длина![]() которого меньше
которого меньше![]() ,
колебание
,
колебание![]() функции
функции![]() меньше
меньше![]() .
.
4. Интегрируемость непрерывных, разрывных и монотонных функций
Теорема:
Непрерывная
на сегменте
![]() функция
функция![]() интегрируема на этом сегменте.
интегрируема на этом сегменте.
Теорема:
Если функция
![]() определена и ограничена на сегменте
определена и ограничена на сегменте![]() ,
и если для любого числа
,
и если для любого числа![]() можно указать конечное число интервалов,
покрывающих все точки разрыва этой
функции и имеющих общую длину меньше
можно указать конечное число интервалов,
покрывающих все точки разрыва этой
функции и имеющих общую длину меньше![]() ,
то
,
то![]() интегрируема на сегменте
интегрируема на сегменте![]() .
.
Следствие:
Ограниченная
на сегменте
![]() функция
функция![]() ,
имеющая лишь конечное число точек
разрыва первого рода, интегрируема на
этом сегменте. В частности, кусочно-непрерывная
на данном сегменте функция интегрируема
на этом сегменте.
,
имеющая лишь конечное число точек
разрыва первого рода, интегрируема на
этом сегменте. В частности, кусочно-непрерывная
на данном сегменте функция интегрируема
на этом сегменте.
Теорема:
Монотонная на
сегменте
![]() функция
функция![]() интегрируема на этом сегменте.
интегрируема на этом сегменте.
5. Основные свойства определенного интеграла
Будем считать, что определенный интеграл с одинаковыми пределами интегрирования равен нулю (по определению):
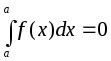 .
.
Будем считать, что при перемене мест верхнего и нижнего пределов интегрирования определенный интеграл меняет знак на противоположный:
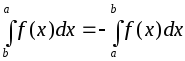 .
.
Пусть функции
 и
и интегрируемы на сегменте
интегрируемы на сегменте ,
тогда функции
,
тогда функции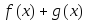 ,
,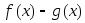 и
и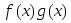 также интегрируемы на этом сегменте,
причем:
также интегрируемы на этом сегменте,
причем:
![]() .
.
Если функция
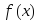 интегрируема на сегменте
интегрируема на сегменте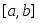 ,
то функция
,
то функция (
(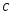 =const)
интегрируема на этом сегменте, причем:
=const)
интегрируема на этом сегменте, причем:
![]() .
.
Если функция
 интегрируема на сегменте
интегрируема на сегменте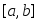 ,
то эта функция интегрируема на любом
сегменте
,
то эта функция интегрируема на любом
сегменте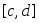 ,
содержащемся в сегменте
,
содержащемся в сегменте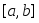 .
.Пусть функция
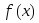 интегрируема на сегментах
интегрируема на сегментах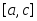 и
и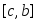 .
Тогда эта функция интегрируема на
сегменте
.
Тогда эта функция интегрируема на
сегменте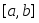 ,
причем:
,
причем:
![]() .
.
6. Оценки интегралов. Формулы среднего значения
Пусть интегрируемая на сегменте
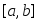 функция
функция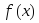 неотрицательна на этом сегменте. Тогда:
неотрицательна на этом сегменте. Тогда:
![]() .
.
Если функция
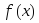 интегрируемая на сегменте
интегрируемая на сегменте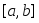 и
и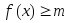 ,
то:
,
то:
![]() .
.
Если функция
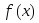 непрерывна, неотрицательна и не равна
тождественно нулю на сегменте
непрерывна, неотрицательна и не равна
тождественно нулю на сегменте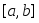 ,
то:
,
то:
![]() .
.
Если функции
![]() и
и![]() интегрируемы на сегменте
интегрируемы на сегменте![]() и
и![]() всюду на этом сегменте, то:
всюду на этом сегменте, то:
![]() .
.
Если функция
 ,
интегрируемая на сегменте
,
интегрируемая на сегменте
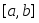 ,
то и функция
,
то и функция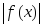 также интегрируема на этом сегменте,
причем:
также интегрируема на этом сегменте,
причем:
 .
.
Пусть функции
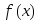 и
и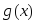 интегрируемы на сегменте
интегрируемы на сегменте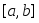 и
и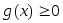 .
Тогда, если
.
Тогда, если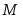 и
и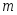 - точные грани
- точные грани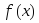 на сегменте
на сегменте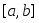 ,
то:
,
то:
![]() .
.
Пусть функция
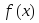 интегрируема на сегменте
интегрируема на сегменте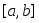 ,
и пусть
,
и пусть и
и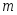 - точные грани
- точные грани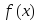 на сегменте
на сегменте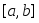 .
Тогда найдется такое число
.
Тогда найдется такое число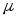 ,
удовлетворяющее неравенствам
,
удовлетворяющее неравенствам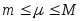 ,
что
,
что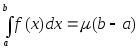 .
.
7. Основные правила интегрирования
Теорема:
Любая непрерывная
на интервале
![]() функция
функция![]() имеет на этом интервале первообразную.
Одной из первообразных является функция:
имеет на этом интервале первообразную.
Одной из первообразных является функция:
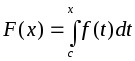 ,
,
где
![]() - любая фиксированная точка интервала
- любая фиксированная точка интервала![]() .
.
Так
как две первообразные данной функции
![]() отличаются на постоянную, то согласно
теореме, любая первообразная
отличаются на постоянную, то согласно
теореме, любая первообразная![]() непрерывной на сегменте
непрерывной на сегменте![]() функции
функции![]() имеет вид:
имеет вид:

где
![]() - некоторая постоянная.
- некоторая постоянная.
Полагая
в последней формуле сначала
![]() ,
затем
,
затем![]() ,
и используя
первое свойства определенного интеграла,
получим:
,
и используя
первое свойства определенного интеграла,
получим:
![]() ,
,
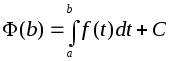 .
.
Из этих равенств вытекает соотношение:
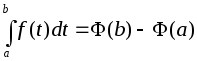 ,
,
которое называется основной формулой интегрального исчисления или формулой Ньютона – Лейбница.
Пусть выполнены следующие условия:
1)
Функция
![]() непрерывна на отрезке
непрерывна на отрезке![]() ;
;
2)
отрезок
![]() является множеством значений некоторой
функции
является множеством значений некоторой
функции![]() ,
определенной на отрезке
,
определенной на отрезке![]() и имеющей на этом отрезке непрерывную
производную;
и имеющей на этом отрезке непрерывную
производную;
3)
![]() ,
,![]() .
.
При этих условиях справедлива формула:
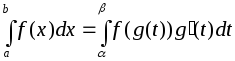
Указанная формула называется формулой замены переменной в определенном интеграле.
Пусть
функции
![]() и
и![]() имеют непрерывные производные на
сегменте
имеют непрерывные производные на
сегменте![]() .
Тогда имеет место следующая формула
интегрирования по частям для определенных
интегралов:
.
Тогда имеет место следующая формула
интегрирования по частям для определенных
интегралов:
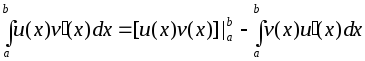 .
.
Так как
![]() и
и![]() ,
то эту формулу можно записать следующим
образом:
,
то эту формулу можно записать следующим
образом:
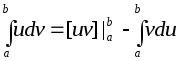 .
.
