
- •Определенные интегралы
- •1. Интегральные суммы
- •3. Равномерно непрерывные функции
- •4. Интегрируемость непрерывных, разрывных и монотонных функций
- •6. Оценки интегралов. Формулы среднего значения
- •7. Основные правила интегрирования
- •8. Приложения определенного интеграла. Площадь плоской фигуры
- •9. Объемы тел вращения
- •10. Несобственные интегралы
- •11. Интегрирование неограниченных функций
- •12. Интегрирование по бесконечному промежутку
- •13. Приближенное вычисление определенных интегралов
- •14. Формула прямоугольников
- •15. Формула трапеций
Определенные интегралы
1. Интегральные суммы
Пусть
функция
![]() задана на сегменте
задана на сегменте![]() ,
,![]() .
Обозначим символом
.
Обозначим символом![]() разбиение сегмента
разбиение сегмента![]() при помощи некоторых несовпадающих
друг с другом точек
при помощи некоторых несовпадающих
друг с другом точек![]() на
на![]() частичных сегментов
частичных сегментов![]() ,
,![]() ,
,![]() ,
,![]() .
Точки
.
Точки![]() ,
,![]() ,
,![]() ,
,![]() будем называть точками разбиения
будем называть точками разбиения![]() .
Пусть
.
Пусть![]() - произвольная точка частичного сегмента
- произвольная точка частичного сегмента![]() ,
а
,
а![]() - разность
- разность![]() ,
которую мы в дальнейшем будем называть
длиной частичного сегмента
,
которую мы в дальнейшем будем называть
длиной частичного сегмента![]() .
.
Определение.
Число
![]() ,
где:
,
где:
![]()
называется
интегральной
суммой (или
суммой Римана) функции
![]() ,
соответствующей разбиению
,
соответствующей разбиению![]() сегмента
сегмента![]() и данному выбору промежуточных точек
и данному выбору промежуточных точек![]() на частичных сегментах
на частичных сегментах![]() .
.
Геометрический смысл интегральной суммы – площадь ступенчатой фигуры.
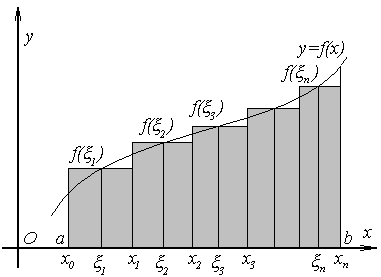
Введем обозначение
![]() .
.
Определение.
Число
![]() называетсяпределом
интегральных сумм
называетсяпределом
интегральных сумм
![]() при
при![]() ,
если для любого положительного
,
если для любого положительного![]() можно указать такое число
можно указать такое число![]() ,
что для любого разбиения
,
что для любого разбиения![]() сегмента
сегмента![]() ,
для которого максимальная длина
,
для которого максимальная длина![]() частичных сегментов меньше
частичных сегментов меньше![]() ,
независимо от выбора точек
,
независимо от выбора точек![]() ,
на сегментах
,
на сегментах![]() выполняется неравенство
выполняется неравенство
![]() ,
т.е.
,
т.е.
![]() .
.
Определение.:
Функция
![]() называетсяинтегрируемой
(по Риману) на сегменте
называетсяинтегрируемой
(по Риману) на сегменте
![]() ,
если существует конечный предел
,
если существует конечный предел![]() интегральных сумм этой функции при
интегральных сумм этой функции при![]() .
Указанный предел
.
Указанный предел![]() называетсяопределенным
интегралом функции по сегменту
называетсяопределенным
интегралом функции по сегменту
![]() и обозначается следующим образом:
и обозначается следующим образом:
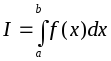 .
.
Числа
![]() и
и![]() называются, соответственно,верхним
и нижним пределом интегрирования,
а отрезок
называются, соответственно,верхним
и нижним пределом интегрирования,
а отрезок
![]() – интервалом интегрирования. В случае
– интервалом интегрирования. В случае![]() определенный интеграл равен площади
криволинейной трапеции, границами
которой являются: ось
определенный интеграл равен площади
криволинейной трапеции, границами
которой являются: ось![]() ,
линии
,
линии![]() и
и![]() ,
а также график функции
,
а также график функции![]() .
Обозначим через
.
Обозначим через![]() и
и![]() соответственно точную верхнюю и точную
нижнюю грани этой функции на сегменте
соответственно точную верхнюю и точную
нижнюю грани этой функции на сегменте![]() .
.
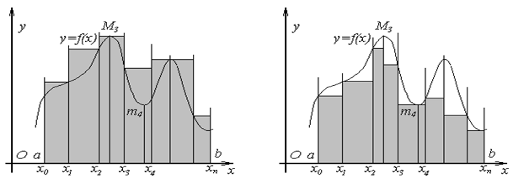
Определение: Суммы:
![]()
![]()
называют
соответственно верхней
и нижней суммами
Дарбу
функции
![]() для данного разбиения
для данного разбиения![]() сегмента
сегмента![]() .
.
Очевидно,
что любая интегральная сумма
![]() данного разбиения
данного разбиения![]() сегмента
сегмента![]() заключена между верхней и нижней суммой
заключена между верхней и нижней суммой![]() и
и![]() этого разбиения.
этого разбиения.
Свойства верхних и нижних сумм:
Для любого фиксированного разбиения
 и для любого
и для любого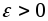 промежуточные точки
промежуточные точки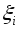 на сегментах
на сегментах можно выбрать так, что интегральная
сумма
можно выбрать так, что интегральная
сумма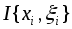 будет удовлетворять неравенствам
будет удовлетворять неравенствам .
Точки
.
Точки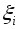 на сегментах
на сегментах можно выбрать также и таким образом,
что интегральная сумма
можно выбрать также и таким образом,
что интегральная сумма будет удовлетворять неравенствам
будет удовлетворять неравенствам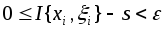 .
.Если разбиение
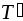 сегмента
сегмента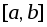 получено путем добавления новых точек
к точкам разбиения
получено путем добавления новых точек
к точкам разбиения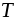 этого сегмента, то для верхних и нижних
сумм этих разбиений выполнены неравенства
этого сегмента, то для верхних и нижних
сумм этих разбиений выполнены неравенства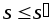 и
и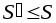 .
.Пусть
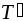 и
и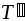 - любые два разбиения сегмента
- любые два разбиения сегмента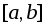 .
Тогда если
.
Тогда если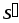 ,
,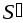 и
и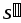 ,
,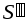 - соответственно нижние и верхние суммы
разбиений
- соответственно нижние и верхние суммы
разбиений и
и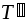 ,
то
,
то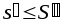 и
и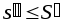 .
.Множество
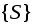 верхних сумм данной функции
верхних сумм данной функции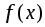 для всевозможных разбиений сегмента
для всевозможных разбиений сегмента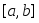 ограничено снизу. Множество
ограничено снизу. Множество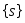 нижних сумм ограничено сверху.
нижних сумм ограничено сверху.
Обозначим
через
![]() точную нижнюю грань множества
точную нижнюю грань множества![]() верхних сумм, а через
верхних сумм, а через![]() - точную верхнюю грань множества нижних
сумм
- точную верхнюю грань множества нижних
сумм![]() .
.
Определение:
Числа
![]() и
и![]() называются соответственно верхним и
нижним интегралами Дарбу от функции
называются соответственно верхним и
нижним интегралами Дарбу от функции![]() .
.
Пусть разбиение
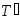 сегмента
сегмента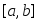 получено из разбиения
получено из разбиения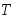 добавлением к последнему
добавлением к последнему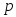 новых точек, и пусть, если
новых точек, и пусть, если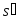 ,
,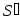 и
и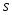 ,
,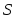 - соответственно нижние и верхние суммы
разбиений
- соответственно нижние и верхние суммы
разбиений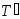 и
и .
Тогда для разностей
.
Тогда для разностей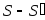 и
и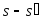 может быть получена оценка, зависящая
от максимальной длины
может быть получена оценка, зависящая
от максимальной длины частичных сегментов разбиения
частичных сегментов разбиения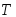 ,
числа
,
числа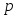 добавленных точек и точных верхней и
нижней граней
добавленных точек и точных верхней и
нижней граней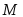 и
и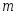 функции
функции на сегменте
на сегменте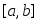 .
Именно
.
Именно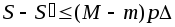 и
и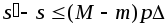 .
.Лемма Дарбу: Верхний и нижний интеграл Дарбу
 и
и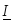 от функции
от функции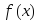 по сегменту
по сегменту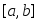 являются соответственно пределами
верхних и нижних сумм при
являются соответственно пределами
верхних и нижних сумм при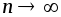 и, следовательно,
и, следовательно,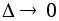 :
:
![]() ,
,
![]() ,
и при этом
,
и при этом![]()
![]() .
.
2. Необходимое и достаточное условие интегрируемости
Теорема:
Для того, чтобы
ограниченная на сегменте
![]() функция
функция![]() была интегрируемой на этом сегменте,
необходимо и достаточно, чтобы для
любого
была интегрируемой на этом сегменте,
необходимо и достаточно, чтобы для
любого![]() нашлось такое разбиение
нашлось такое разбиение![]() сегмента
сегмента![]() ,
для которого
,
для которого![]() .
.
Определение:
Число
![]() называется колебанием функции
называется колебанием функции![]() на сегменте
на сегменте![]() .
.
Так
как
![]() ,
то
,
то![]() .
Далее запишем
.
Далее запишем![]() в следующей форме:
в следующей форме:
![]() .
.
Теорема:
Для того, чтобы
ограниченная на сегменте
![]() функция
функция![]() была интегрируемой на этом сегменте,
необходимо и достаточно, чтобы для
любого
была интегрируемой на этом сегменте,
необходимо и достаточно, чтобы для
любого![]() нашлось такое разбиение
нашлось такое разбиение![]() сегмента
сегмента![]() ,
для которого
,
для которого![]() .
.
Другими
словами, необходимым
и достаточным условием интегрируемости
функции на промежутке
![]() является выполнение условия
является выполнение условия
![]()
![]() ,
или
,
или
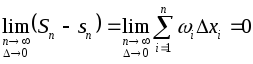 ,
где
,
где![]() .
.
