§3 П. 16, 17 № 14, 15 с.35

Лекційно-практичне заняття 3

Перпендикулярність прямих і площин в просторі

Тема. Перпендикуляр і похила. Відстань від прямої до паралельної площини. Теорема про три перпендикуляри. Самостійна робота.

План

1. Перпендикуляр і похила.

2. Відстань від прямої до паралельної площини.

3. Теорема про три перпендикуляри.

Література

1. Погорєлов О.В. Геометрія. Стереометрія. Підручник за 10-11 кл. Київ : Освіта, 1994 – 128с.

2. Афанасьєва О.М., Бродский Я.С., Павлов О.Л. Геометрія 10 -11кл. : Пробний підручник. – Тернопіль: Навчальна книга – Богдан, 2004

Перебіг заняття

1. Перпендикуляр і похила

Нехай дано площину і точку, яка не лежить на ній (рис.1).

Перпендикуляром, опущеним з даної точки на одну площину, називається відрізок, що сполучає дану точку з точкою площини і лежить на прямій, перпендикулярній до площини (АС).

Кінець цього відрізка, який лежить у площині, називається основою перпендикуляра (С).

Відстанню від точки до площини називається довжина перпендикуляра, опущеного з цієї точки на площину (АС).

Похилою, проведеною з даної точки до даної площини, називається будь-який відрізок, який сполучає дану точку з точкою площини і не є перпендикуляром до площини (АВ).

Кінець відрізка, що лежить у площині, називається основою похилої (В).

Відрізок, який сполучає основи перпендикуляра і похилої, проведених з однієї і тієї самої точки, називається проекцією похилої (ВС).

Рис.1

2. Відстань від прямої до паралельної площини

Означення. Відстанню від прямої до паралельної їй площини називається відстань від будь-якої точки цієї прямої до площини.

Означення. Відстанню між паралельними площинами називається відстань від будь-якої точки однієї площини до другої площини.

3. Теорема про три перпендикуляри

Теорема 7. Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна до похилої.

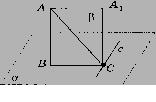Дано:

.

Довести: .

Доведення

Через точку С і пряму АВ проводимо і в ній . Оскільки і, то .

Оскільки , то, отже, сАС .

Теорема 8. Якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої.

Дано:

Довести: с ВС .

Доведення

Через точку С і пряму АВ проводимо і в нійА₁С : А₁С АВ . Оскіль­ки і,то .

Оскільки АС с , , то, отже, .

4. Закріплення та осмислення вивченого матеріалу

1. Знайти довжину похилої, якщо довжина перпендикуляра дорівнює 4 см, а проекція похилої на площину — 3 см.

2. Знайти проекцію похилої на площину, якщо похила дорівнює 13 см, а перпендикуляр, проведений з тієї ж точки, — 12 см. Знайти довжину перпендикуляра, якщо похила дорівнює 10 см, а її проекція на площину — 8 см.

3. Скільки перпендикулярів можна опустити з даної точки до даної площини? Чому?

4. Скільки похилих можна провести з даної точки до даної площини? Як слід установити на хрестовині ялинку, щоб вона була перпенди­кулярна до площини підлоги?

5. Як на практиці за допомогою виска перевірити вертикальність встановленого стовпа?

7. Із точки проведено до площиниперпендикулярта похиліSА і SВ. Довжини похилих відповідно дорівнюють 13 і 20 см. Дов­жина проекції похилої АS дорівнює 5 см (рис. 2). Знайти від­стань від точки S до площини та довжину проекції похилої SВ.

Рис.2

8. Знайти відстань від точки А до граней куба, якщо ребро куба дорівнює 10 см.

9. Задача №22 (підручник с. 36).

10. Задача №23 (підручник с. 36).

Відповідь: 6 см, 15 см.

11. Задача №25 (підручник с. 36).

Відповідь: 9 см.

12. Задача №28 (підручник с. 36).

Контрольні запитання

• Що таке перпендикуляр, опущений з даної точки до площини?

• Що таке похила, проведена з даної точки до площини?

• Дайте означення відстані від прямої до паралельної їй площини.

• Сформулюйте теорему про три перпендикуляри.

Домашнє завдання

1) §3 п. 18 № 24 с.36.

п. 19 № 27 с.36.