ГОС / MODUL_1_matematika

М1_1. Клас-е опр-е вт-и, аксиомы теории в-ти. Формулы полной вероятности и Байеса.

Опр. Мн-во Е взаимоисключающих исходов эксперимента, наз. пр-вом эл-ных событий.

Опр. Эл. событием наз элемент Е

Опр. Событием, наз мн-во АЕ

Опр. События А и В наз несовместными, если А∙В=ø, Е наз достоверным событием, ø – невозможным событием.

Пусть Е – пр-во элем событий

Опр. Говорят, что на Е заданы в-ти, если определена ф-ция Р действующая из Е в R такая что 1) р(е)≥0, 2) .

Опр. Вер-тью события А наз число р(А)=

Св-ва в-ти:

1. р(ø)=0, р(Е)=1,

2.Для любого A,BєF, р(А+В)=р(А)+р(В)-р(АВ)

Д-во: A+B=(A-AB)+(B-AB)+AB: т.к. эти события несовместны, то p(A+B)=p(A-AB)+p(B-AB)+p(AB)+p(AB)-p(AB)=p(A)+p(B)-p(AB)

следствие: если А и В несовместны, то р(А+В)=р(А)+р(В)

док: р(А+В)=р(А)+р(В)-р(АВ)=<р(АВ)= ø >= р(А)+р(В)

3.Для любого AєF р()=1-р(А)

Д-во: А+=E p(A)+p()=p(E)=1

P()=1-1-p(A)

4. Для любого A,BєF, такая что A B вып-ся p(A)<=p(B).

B=A+B

P(B)=p(A)+p(B)>=p(A)

5. Для любого AєF выполняется p(A)<=1.

Классич-е опред-е в-ти.

Пусть Е пр-во эл-ных событий все исходы кот равновероятны состоит из n элементов

р(А)= (число эл А)/n = (число благоприятных исходов)/(на общее число исходов).

Л1: если элем. аєА можно выбрать n способами, а эл-т bєВ можно выбрать m способами, то элемент (а,b) можно выбрать nm способами. А если аb= ø, то элемент (неупорядоченный) (а,b) можно выбрать mn способами.

Перестановки:

Опр: пусть дано мн-во {а₁, … ,а_n}, установленный на мн-ве порядок наз перестановкой.

Р(n)=n!

Опр. Неупорядоченное подмн-во из m элементов данного мн-ва наз (m≤n) сочетанием из n элементов по m. Число сочетаний можно рассчитать по формуле

.

Опр: упорядоченное подмн-во из m элементов данного мн-ва (m≤n) наз размещением (разм-ем) из n элементов по m.

Разм-ния бывают без повторений и с повторением.

Число разм-ий без повторений можно рассчитать по ф-ле . Число разм-ний с повторением равно =n^m

Аксиомы теории вер-ти

Опр. С-ма F подмн-во Е наз. Алгеброй, если: 1) Е принадлежит F, 2) для любого А принадл. F и для любого B принадл. F выполн. А+В принадл.F и А*В принадл. F 3) для любого А принадл. F выполн.

Опр. Вер-тью событий наз. ф-я р:F->R, такая что

1) А принадл. F, P(A)>=0

2) P(E)=1

3) (А_n)_n€N такой что А_i*A_j =Ø при i<>j выполн. <E, F, P> наз. Вероятностное пространство

6.Т: (о непрерывности вероятности): для того чтобы (А_n), n єN и так чтобы А_iА_j= ø выполнялось р()=необ и дост чтобы (В_n),n єN, так чтобы В_n+1 В_n,=В выполнялось lim р(В_n)=р(В), при n→∞.

Услов-я вер-ть. Независимость событий.

Опр: Пусть<,F,р>- вероятностное пр-во, А и В события, причем р(В)>0, тогда вероятностью события А при условии, что событие В уже произошло наз число р(А/В)=р(АВ)/р(В).

Опр: Событие А и В наз независимыми, если р(А/В)=р(А).

Следствие: Если А и В независимы, то р(АВ)=р(А)р(В)

Формула полной вер-ти.

Т: пусть А– некоторое событие; В₁,В₂,…,В_n имеют положительные вероятности, попарно несовместные и такие что А, тогда имеет место формула полной вероятности.

р(А)=р(В_i)р(А/В_i).

Док-во: А, → А=А=АВ_i.

р(А)=р(АВ_i)= =р(АВ_i)= (т.к. событ-я несовместны, то) <р(С/Д)=р(СД)/р(Д))>= р(В_i)р(А/В_i). Ч.т.д.

Схема решения задач на вычисление полной вероятности.

1.уяснить послед-ть испытаний рассм-мых в задаче.

2.обозначить событие, вер-ти к-рого нужно найти А.

3. составить попарно несовместные гипотезы В₁,В₂,…,В_n

4.Вычислить р(В_i), р(А/В_i),i=1,…,n

5. По ф-ле полной вер-ти найти р(А).

Ф-ла Байеса.

Пусть событие А может наступить только с одним из n попарно несовместных событий В₁,В₂,…,В_n. Пусть произойдет опыт и событие А наступило. Найти вер-ть выполнения гипотезы В_i, если событие А произошло.

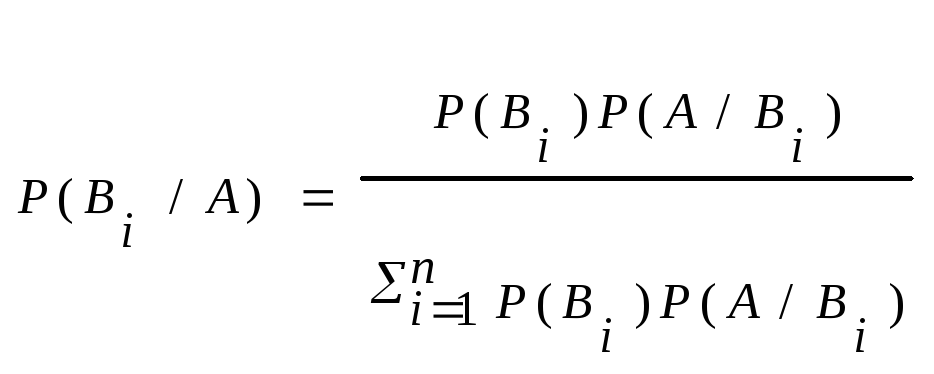
– Формула Байеса

Док-во:

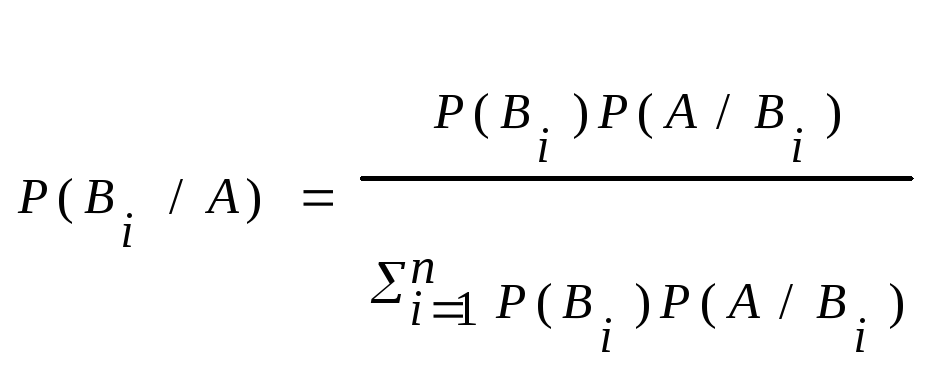
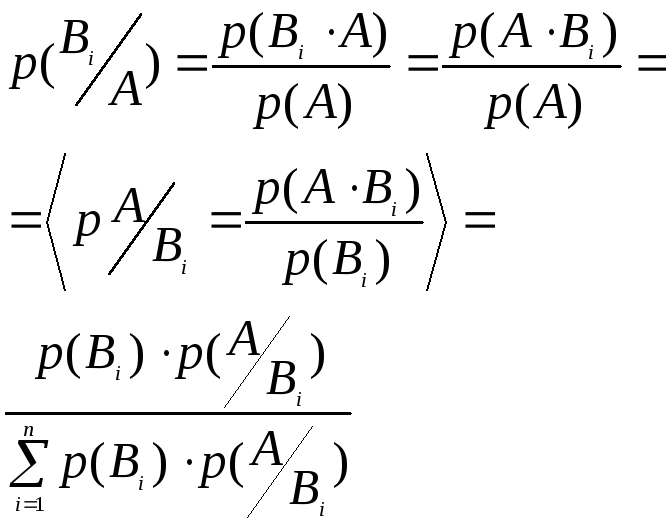М1. –М1 - 2. Задачи матм-й статистики. Проверка гипотез.

Задачи МС возникают тогда, когда нужно найти закон распред-я предметов по нек-му признаку. Напр, закон распр-я людей по возрасту и т.д. Для реш-я таких задач вводят случ-ю величину х, закон расп-я к-рой нужно найти и из всей совок-ти предметов выбирают произвольную и достаточно большую часть к-рой наз-т выборкой. Выборка должна удовл-ть 2-м св-вам: 1) достаточно большой; 2) произвольная.

МС занимается разработкой приёмов стат-ких наблюдений и анализом стат-ких данных.

Основные з-чи МС

1. Задача ставится так: в результате N незав-х испытаний над случайной величиной X получены следующие её значения: x₁, x₂, … , x_n. Требуется опред-ть, хотя бы приближённо, неизвестную ф-цию распред-я F(x) этой случайной величины.

2. Пусть из общих соображений F(x) известная ф-ция распред-ния некоторой случ-й величины. По результатам N незав-х испытаний: x₁, x₂, …, x_n требуется оценить параметры этого распред-я и точность этих оценок. Напр, установить числовые знач-я мат-го ожидания и дисперсии этой случ-й величины X.

3. З-ча ставится так: на основании нек-рых соображений выдвигается гипотеза о виде распред-я или о парам-х распред-я нек-рой случайной величины. Спрашивается, совместимы ли результаты наблюдений x₁, x₂, … , x_n с выдвинутой гипотезой.

Эмпирический закон распр-я.

Введем случ-ю величину х, закон распр-я нужно получить. Проведем n опытов. Пусть значение х₁ принимает m₁ раз, х₂ принимает m₂ раза, и т.д.

На практике очень редко встреч-ся случаи, когда закон распр-я не известен полностью. Обычно не известен какой-то параметр θ. Приближенное знач-е этого параметра называется оценкой, - оценка, она должна удовлетворять двум условиям: 1) М[]= θ; 2) D[] →0 при n→∞

Оценки удовлетв-щие условиям 1 и 2 называются состоятельными.

Опр: Пусть ξ – дискретная случайная величина, тогда мат-е ожидание ξ – наз числа M[ξ]= ξ₁p₁+ ξ₂p₂+…

Опр: Пусть <Ω,F,p> - вероятностное пр-во случайной величиной ξ: Ω →R (измеримая, т.е. такая, что для любого борелевского мн-ва В из R ξ^-1(В) єF

ξ^-1(В)={x: ξ(x) єB} xє Ω

Закон больших чисел.

Факт приближения средних характеристик большого числа опытов, к некоторой определенной постоянной.

Первое нер-во Чебышева

Пусть случайная величина х неотрицательна и имеет математическое ожидание M[x], тогда p(x)>=1, M[x]>=1.

Нормальное распр-е.

Закон нормального распр-я, если случайная величина имеет плотность вероятности р(х)=.

Выясним, какой смысл имеют параметры G и а.

M[x]=a; D[x]=M[(x-M[x])²]=M[(x-a)²] G²=D[x]

Равномерное распред-е.

Опр: случайная величина х имеет закон равном-го распр-я, если случ-я величина имеет плотность вероятности р(х)=; 1==с(а-b)

с=1/(b-а).

Закон равном-го распр-я имеет место там, где случ-я величина принимает знач-е из [а,b]. Причем все знач-я из [а,b] равномерные.

Дисперсия (Д) и ее св-ва.

Опр:Д. случ-й величины ξ наз. число D[ξ]=M[(ξ-M[ξ])²]

Св-ва: 1)D[ξ]=M[ξ²]-(M[ξ])². 2)D[ξ]=0 P(ξ=c)=1

3)D[c ξ]=c²D[ξ].

4) Если случ-я величина ξ и η независимы, то D[ξ+ η]=D[ξ]+D[η]

Опр: если случ-я величина ξ не явл-ся дискретной и F (ξ) ее ф-ция распр-я, то M[ξ]= ξdF(ξ)

Опр: Медианой выборки наз-ся число, к-рое делит упоряд-е мн-во данных чисел пополам.

Опр: Модой наз-ся число, к-рое встечается в выборке найболее часто.

Опр: Разбросом выборки наз-ют число, равное x_наиб.-x_наим.

Второе неравенство Чебышева

Пусть случайная величина х имеет математическое ожидание M[x], и дисперсию D(x), тогда

Непрер-я случ величина

Опр: случ-я величина ξ наз непрер-ой, если ее ф-ция распред-я F _ξ(х) непрерывна для всех х.

Элементы проверки статистич-х гипотез

Опр. Статистич-й гипотезой наз-ся любое предполож-е о виде или параметрах неизвестного закона распр-я.

Пусть имеется случ-я величина ξ с неизвестной ф-ей распр-я, связанная с генеральной совок-ю. Выдвигается гипотеза H – случ-я величина ξ имеет конкретное распр-е. Требуется по выборке объёма n: (x₁, x₂, … x_n) решить – принять или отвергнуть эту гипотезу.

Критерии, к-рые позволяют это делать, называют крит-ми согласия.

Крит-и значимости.

Имеется случ-я величина ξ, связанная с ген-ой совок-ю, распр-ние к-рой неизвестно. Требуется оценить нек-е её числовые характер-ки, т. е. проверить гипотезу Н, состоящую в том, что нек-рая числовая характ-ка случ-й величины ξ равна ранее заданному числу, напр, требуется по выборке объёма n (x₁, x₂, …, x_n) проверить, что Mξ=m₀ и т.п.

Крит-и, к-рые позволяют это сделать, наз-ся крит-ми значимости.

Прив-м нек-рые крит-и знач-ти.

1) Крит-и значимости для нахождения ср-го знач-я случ-ной величины ξ.

2) Крит-и знач-ти для сравнения ср-х знач-й 2х случ-х величин.

3) Крит-и знач-ти, основанные на стандартных ошибках.

Статистич-я проверка гипотезы по закону распредел-я.

Опр: Гип-зу H₀ наз-м гип-зой о сходстве, а альтернат- ю гип-зу о различаи наз-м H₁.

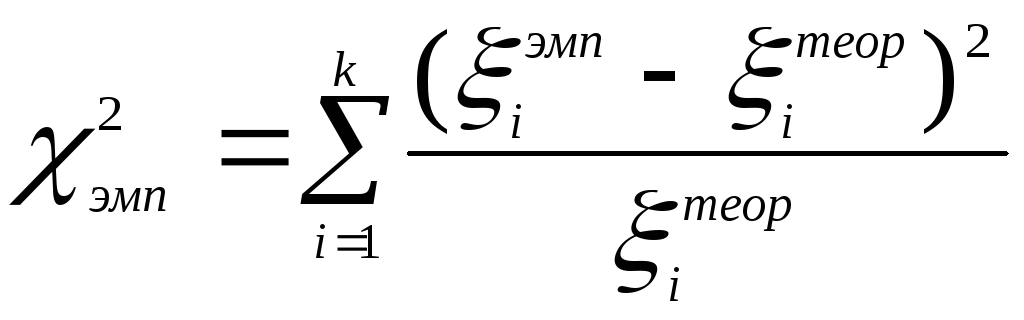Возьмем случ-ю величину ξ и проведем k опытов. Пусть в этих оытах ξ прин-ет знач-я: . В то же время по предпол-ю ξ д.б. принимать знач-е . Находим . В таблице распред-я χ² для знач-я ν=k-1 (число степеней свободы) выбирается χ²(критериал-е)(0,05) или χ²(критериал-е)(0,01). Чертим ось значим-ти:

Случ.1. Если χ² попало в зону эмпир-кой знач- ти, то применим гипотезу H₀ (об отсутствии отличий).

Случ.2. Если χ² попало в зону знач-ти, то прим-ем гип-зу H₁ (о наличае различий).

Случ.3. Если χ² попало в зону неопредел-т, то вывод сделать нельзя и нужно увеличить кол-во опытов. Критерий χ² примен-ют при проверке различий м/у 2-мя выборками.