Строгий учет погрешностей по способу границ.

Теорема 1 Нижняя граница суммы равна сумме нижних границ слагаемых; верхняя граница суммы равна сумме верхних границ слагаемых.

Доказательство: пусть у чисел х и у указаны их нижняя и верхняя границы, и пусть НГх=l1, ВГх=L1, НГу=l2, ВГ=L2. Запишем виде неравенства: l1<=x<=L1, l2<=y<=L2. (*) Используя теорему о почленном сложении неравенств, получим: l1+l2<=x+y<=L1+L2. Отсюда НГх+у=НГх+НГу, ВГх+у=ВГх+ВГу.

Теорема 2 Нижняя граница разности равна разности между нижней границей уменьшаемого и верхней границей вычитаемого; верхняя граница разности равна разности между верхней границей уменьшаемого и нижней границей.

Доказательство: (аналогично теореме 1).

Теорема 3 Нижняя граница произведения равна произведению нижних границ сомножителей, верхняя граница произведения равна произведению верхних границ сомножителей.

Доказательство:

Будем считать, что l1>0, l2>0. Почленно перемножая неравенства (*), получим l1*l2<=xy<=L1*L2. Отсюда НГху=НГх*НГу, ВГху=ВГх*ВГу

Теорема 4 Нижняя граница частного равна частному от деления нижней границы делимого на верхнюю границу делителя; верхняя граница частного равна частному от деления верхней границы делимого на нижнюю границу делителя.

Теорема 5 Нижняя граница степени равна той же степени нижней границы основания ; верхняя граница степени равна той же степени верхней границы основания.

Теорема 6 Нижняя граница корня равна корню из нижней границы подкоренного числа; верхняя граница корня равна корню из верхней границы подкоренного числа.

Чм(5). Числен методы Реш-я нелин-х урав-ий

Для большинства уравнений вида (1), где нелинейная ф-ция одной перем-ой, не сущ-ет аналитич-х выражений (формул) для вычисления их корней. Поэтому приходится применять различные численные методы для отыскания корней ур-я (1). Поэтому для отыскания корней ур-ия (1) применяют различные численные методы. Будем рассм-ть ф-ции , имеющие только изолир-ные корни. Отыскание корня ур-я (1) выполняется в 2 этапа:

1)отделение корня, т.е. выбор промежутка, в котором находится единств-й корень;

2) уточнение корня, т.е. вычисление приближенного значения с заданной точностью.

Достаточное условие сущ-ия корня функции на замкнутом промежутке дает теорема Больцано-Коши.

Теорема: Если функция определена и непрерывна на замкнутом промежутке [a, b] и на концах его принимает значения разных знаков, , то между a и b найдется по крайней мере один корень функции , т.е. найдется точка c, a<c<b, для .

Отделение корня можно провести графически или аналитически.

Граф.: представим ур-е (1) в виде f ₁(x)= f ₂(x). Построим графики ф-ий y= f ₁(x) и y= f₂(x). Абсцисса точки пересечения этих графиков и будет приближенным решением ур(1).

Уточнение корня можно провести одним из следующих методов.

Метод хорд

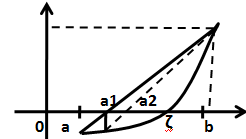
Идея метода: дуга кривой , соединяющая точки (a,f(a)) и (b,f(b)), заменяется хордой, проходящей через эти точки. В качестве приближенного значения корня ур-я(1) берется абсцисса a₁ точки пересечения хорды с осью ОХ.

Корень ур-я (1) будет находиться между a₁ и одним из концов промежутка [a, b] в зависимости от свойств функции f(x). Выбрав часть отрезка, содержащую корень (в нашем случае [a₁,b]), осуществим такое же построение и получим точку a₂ и т.д. В результате получаем послед-ность приближенных значений , монотонно сходящуюся к точному значению корня ζ.

Отметим, что один из двух концов промежутка один (в нашем случае b) неподвижен. Неподвижным является тот конец отрезка [a,b], для кот-о выполн-ся усл f(x)*f ”(x)>0, т.е. знак ф-ии в точках a и b совпадает со знаком производной. Последов-ные приближения лежат по ту сторону корня, где ф-ия f(x) имеет знак, противоположный знаку ее 2-ой производной. Возможны следующие случаи для [a,b]:

1. f(b)*f ‘’(x)>0 – точка b – неподвижная.

2. f(b)*f ‘’(x)<0 – точка a неподвижная.

Рассмотрим сл1:

f(b)*f ‘’(x)>0, когда f(b)>0,

f ‘’(x)>0.

Пусть ζ - истинный корень ур-я. Ур-е хорды:

;;

…

В результате имеем а< a₁ <a₂ <…<a_n+1<…< ζ<b монотонно возрастающую огранич. сверху послед-ть, значит она имеет предел. Общий случай: Так как ζ – истинный корень ур-я, то , тогда Для оценки точности приближения используют формулу: Формула, позволяющая оценить абсолютную погрешность приближ-ного значения х_n, если известны 2 последов-ых приближения х_n-1 и x_n

Пусть f ‘ (x) непрерывна на [a,b], содержащем все приближения, и сохраняет свой знак, причем 0<m₁≤|f ‘ (x)|≤ M₁<+∞ и пусть

Тогда

Так как

(**)

Так как f ‘(x) на [a,b] сохраняет свой знак и , то и из формулы (**) имеем

Если [a,b] узок, то имеет место нер-во M₁≤ 2m₁. Из (***) имеем |x_n-x_n-1|<ε. => |x_n-ζ|<ε.