ЧМ(1). Реш сис лин.ур

Метод итерации. Пусть дана след. сист. лин-х ур-й (1), где ,. Предполагая, что разрешим ее отн-но (2), где , , при , , при . Сис. (2) можно записать =Т+ (2’), Т+-можно расс-ть как отображение Φ, переводящее элемент n - го прост-ва в того же прост-ва. При этом . Вопрос о решении системы (2’) сводится к отысканию неподвижной точки отобр-ия Ф, опред-ого формулой . Если отображение сжимающее в смысле какой либо метрики n - го векторного прост-ва, то решение у-я =Т+ может быть получено методом послед-ных приближений. Послед-ные приближения ищутся по формуле: =Т+,, k =1, 2,…(3), начиная с произвольного. При каких же условиях отображение Ф будет сжимающим?

Опр: Мно-во М элементов произвольной природы наз-ся мет. пр-ом, если каждой упоряд-ой паре (x; y) из М поставлено в соответствие , которое уд. следующим св-ам:

1) <=> x = y; 2);

3) .

Опр: Пусть M – метрическое простр-во. Отображение А прост-ва M в себя наз-т сжимающим, если сущ. такое , что справедливо: .

Опр. Послед-ть точек метрического прост-ва М наз-ся фундаментальной, если она удов-ет критерию Коши: Опр. Если в метрическом прост-ве М всякая фундаментальная пос-сть сходится к точ. , то пр-во М наз-ют полным.

Ответ зависит не только от самого отображения, но и от выбора метрики в n - ом прост-тве. Рассмотрим 3 варианта:

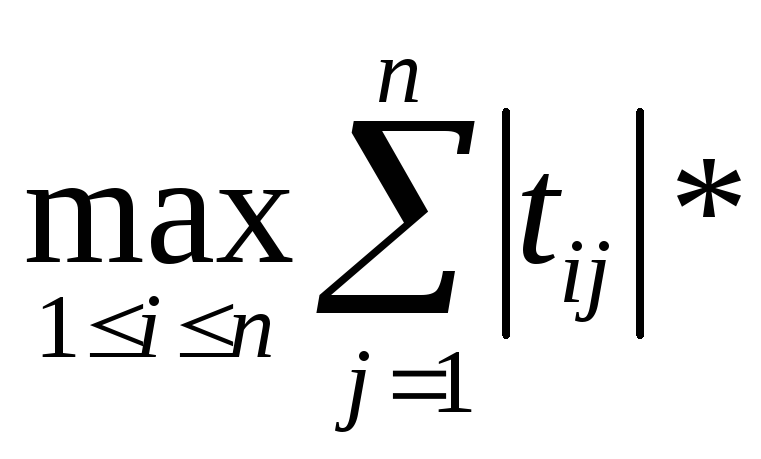
1) Пусть метрика введена след. образом: (4). Как известно, n - ое векторное пространство полно в смысле метрики (4). Рассмотрим = = Если элементы матрицы Т удов-ют усл., то отображение п-мерного вектор. прост-ва в себя, опред-го оператором Ф=Т+ явл-ся сжимающим в смысле метрики (4). Т.к. n-мерное вектор. про-во с метрикой (4) – полное, то в силу принципа сжимающих отображ., отображ-е Ф имеет единст-ую неподвижн.точку. След. Сис. (2) имеет един. .реш-е, которое м. быть получено как предел последовательности (3).

2)

3)

Мет Зейделя.

Идея: вычисление (к+1)-го приближения неизвестной хi учитывает уже вычисленные ранее (к+1)-е приближения неизвестных (х1, х2…х i-1)/

Пусть дана система . Сведм эту систему к =Т+ . можно выбрать произвольные начальные приближения корней.

Предполагая что к-е приближение известно, будем искать (к+1)-е по формулам:

Мет. Гаусса Идея этого метода заключается в том, чтобы исходную систему лин. у-й (1) с произвольной матрицей А свести некоторыми экв-ми преобр-ями к сис. вида (2), где - треугольная матрица. Алгоритм решения сис-мы (2) след-й: из последнего у-я находится , затем из предыдущего - и т. д. Пример: Дана сис. Из 4 урав-й с четырьмя неизвестн (1) Матрица А

невырожденная. Пусть а₁₁ ≠0 (ведущий элемент). Разделив коэфф. 1 уравнен. сис.(1) на а_11, получим (2), где . Из каждого из остальных урав. вычитается 1, умножен. на соответ-й коэфф. a_i1.В результ х₁ оказывается исключенным из всех урав-й, кроме первого (аналогично исключ. х_2, . . ., х_n). Процесс сведения сис.(1) к системе с треуг. матрицей наз-ся прямым ходом метода Гаусса. Находим реш-е получившейся сис. обратным ходом метода Гаусса.

Чм(2)Численное интерполирование

Функция f(x) задана таблицей, те. y_i=f(x_i), где i=1..n. Нужно построить аналитическую функцию, описыв-ую св-ва заданной функция. Решим задачу построением интерполяционного полинома. Для этого выберем класс линейно независимых функций вида:₁(x), ₂(x), _n (x). Составим линейную комбинацию с постоянными коэффициентами, где с_i -постоянная. Потребуем, чтобы R_n(x_i) = f(x_i)(1). Система (1) n-уравнений с n-неизвестными с_i, имеет единственное решение, т.к. опреде­литель, составленный из коэффиц-ов при неизвестных не равен нулю. Значит, можно построить единств-ый интерполяционный полином, пе­редающий свойства заданной функции f. R_n(x)  f(x). Точки x₁,…,x_n наз-ся узлами интерполяции. Будем предполагать, что x₁< x₂<…<x_n. Многочлен R_n(x) будем наз интерполирующим. Процесс построения интерполяционного полинома наз-ся интерполяцией. Геометр-ки интерполирование означает: найти кривую у = R_n(x) определенного типа, проходящую через заданную систему точек M_i(x_i, y_i).

Выбор в качестве интерпо-щей функции полинома основан на свойствах многочленов в классе непрерывных функций:

1Свойство полноты: если функция f непрерывна на конечном замкнутом промежутке [а, b], то  > 0 можно указать такой многочлен R_n(x), что f(x) - R_n(x)  <  для x[а, b].

2° Свойство простой природы: значение многочлена можно вычислить за конечное число шагов.

Конечные разности

Пусть функция f(x) задана в точках x_i = x₀ + x_ih, где x_i - узлы интерполяции, h - шаг интерполяции. Составим разности значений функции:

у₁ – у₀ = f(x₀+h)-f(x₀)=Δf(x₀)= Δy_{0……………..}

y_n-y_n-1=f(x_n-1+h)-

f(x_n-1)=Δf(x_n-1)= Δy_n-1.

Конечными разностями первого порядка наз-т приращение функции при переходе от одного узла интерполяции к следующему.

Δy₀- Δy₁= Δ² y₀

Δy_n-1- Δy_n-2= Δ² y_n-2

Конечными разностями второго порядка наз-ют приращение конечных разностей первого порядка при переходе от одного узла интерполяции к следующему.

Аналогично конечными разностями n-го порядка наз-т приращение конечных разностей n-го порядка при переходе от одного узла интерполяций к следующему. Простейшие св-ва конечных разностей:

1f – const, то Δf = 0

2Δ(сf)=cΔf

3Δ(f₁ + f₂)=Δf₁ + Δf₂

4Δ^m(Δⁿf)=Δ^m+nf

5° конечная разность n-го порядка от многочлена степени n есть пост. величина. Сле­д-но, конечные разности порядка выше n равны нулю.

Первая интерполяционная формула Ньютона. Пусть функция задана таблично y_i = f(x_i ) x_i = x₀ + ih, где h – шаг интерполяции. Требуется построить полипом P_n(x) такой, чтобы P_n(x_i) = y_i (1) и степень его была бы не выше n. Условие (1) эквивалентно Δ^mP_n(x) = Δ^my₀ (2). Полином будем искать в виде: P_n(x)=a₀+a₁(x-x₀)¹+…+

a_n(x-x₀)^[n](3). Задача состоит в отыскании коэффициентов a₀, a₁,…, a_n.Пусть x = x₀. Тогда, a₀ = P_n(x₀) = y_0, чтобы найти послед. коэффициенты будем находить конечные разности полинома P_n(x):

ΔP_n(x) = a₁h + 2 a₂h(x-x₀)1+…+na_nh(x-x₀)^[n-1]

При x = x_0,

ΔP_n(x₀)=a₁h, ΔP_n(x₀)= Δy₀a₁= Δy₀/h.

Δ²P_n(x) =1*2*a₂h² + 3*2a₃h²(x-x₀)^[1]+.+n(n-1)* a_n* h²(x-x₀)^[n-2].

Полагая х=х₀:

Δ²P_n(x₀) = 2!a₂h²a₂ = Δ²y₀/2!h² и т.д. a_k = Δ^ky₀/k!h^k. Подставим в (3), получим:P_n(x) = y₀+(x-x₀)^[1]Δy₀/h+(x-x₀)^[2]Δ²y₀/2!h²+…+(x-x₀)^[n]Δⁿy₀/n!hⁿ

Полином полностью удовл-ет треб-ям поставленной задачи. Для практич использования положим q=(x-x₀)/h, тогда P_n(x)=y₀+qΔy₀+(q(q-1)Δ²y₀)/2!+ +…+(q(q-1)…(q-(n-1))*Δⁿy₀)/n! (4) - это окончательный вид первой интерпол-ной формулы Ньютона. Формулу (4) выгодно использовать для интерполирования функции

у=f(x) в окрестности начального значения x₀. Если таблица значений функции конечна, то число n ограничено, а именно: n не может быть больше числа значений функции у, уменьшенного на единицу Если дана неограниченная таблица значений функций у, то n выбирают так, чтобы |Δⁿy_i< . где - заданная погрешность интерполирования. Если дана таблица значений некоторой функции с шагом h и нужно найти значение функ­ции для некоторого значения х, наход-гося м|у х_i и х_i+h, то за x₀ принимаем число x_i.

Оценка погрешности для 1-ой интерпол-ной формулы Ньютона:

R_n(x)  q(q-1)(q-2)…(q-n+1)Δⁿ⁺¹y₀/(n+1)!

Вторая интерп-ная формула Ньютона P_n(x)= y_n+qΔy_n-1+ +q(q+1)Δ²y_n-2/2!+ ...+q(q+1)…(q+n-1)* Δⁿy₀/n!

Оценка погрешности для второй интерполяционной формулы Ньютона

R_n(x)q(q+1)(q+2)(q+n)*Δⁿ⁺¹y_т/(n+1)!