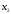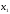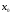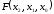9. Кнф, днф, сднф, скнф. Функционально полные системы логических функций

Приведенная в таблице 2.3 система шестнадцати элементарных функций составляет максимальную систему. Однако каждую элементарную логическую функцию можно записать с помощью только функций И, ИЛИ, НЕ в дизъюнктивной или конъюнктивной нормальных формах. Следовательно, существуют наборы логических функций, с помощью которых можно реализовать все остальные логические функции. В частности, такими наборами являются:

1. И, ИЛИ, НЕ;

2. И–НЕ;

3. ИЛИ–НЕ.

Система таких логических функций называется функционально полной. В современной интегральной микросхемотехнике преимущественное распространение системы И–НЕ, ИЛИ–НЕ и И, ИЛИ, НЕ получили в силу просторы преобразований, выполняемых с этими функциями, способности иметь большое число входов, минимума логических элементов.

СДНФ функции, представленной в таблицей истинности 2.4 или уравнением (2.19) в аналитической форме, легко может быть преобразована в структурную логическую схему, если операции И, ИЛИ, НЕ, описывающие эту функцию, представить в виде логических элементов, реализующих эти операции. При этом каждая конституента единицы реализуется в виде элементов И, на входы которых поданы соответствующие значения переменных, а выходы элементов И, реализующие все конъюнкции, объединяются общим элементом логического суммирования ИЛИ. Структурная схема этой функции представлена на рис. 2.1.

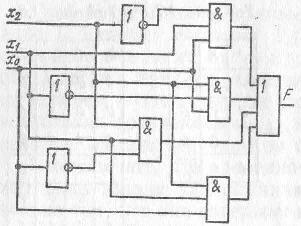
Рис. 2.1. Структурная схема функции, заданной выражением (2.19)

Однако в подавляющем большинстве случаев структура схемы, реализующей функцию ее в СДНФ или СКНФ, является избыточной и может быть существенно упрощена на основании ряда формальных операций, которые называются минимизацией логических схем. Целью минимизации является получение логической схемы, содержащей минимальное число логических элементов с минимальным числом входов.

Наиболее широкое распространение в силу своей простоты и наглядности получили способы, использующие карты Карно или Вейча. Эти карты представляют собой таблицы истинности, преобразованные таким образом, что у функции, нанесенной на такую карту, соседние конъюнкции находятся либо рядом, либо на заранее известных местах.

Карты Карно для двух, трех и четырех переменных приведены на рис. 2.2.

Рис. 2.2. Карты Карно для двух, трех и четырех переменных

Карты Карно для пяти и более переменных рассматриваются как состоящие из отдельных подкарт для четырех переменных: для 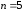– из двух подкарт, для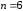– из четырех подкарт и т.д.

Для поиска соседних конъюнкций на карту Карно необходимо сначала нанести функцию, т.е. поставить на местах десятичных номеров той или иной карты значения логической функции на этих номерах наборов. Например, для функции, приведенной в таблице 2.4, выбираем карту Карно для трех переменных и на местах наборов 3, 5, 6, 7 ставим единицы, а на остальных нули (рис. 2.3)

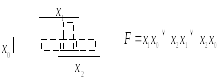
Рис. 2.3. Минимизация с помощью карты Карно функции (2.19)

Порядок операций при минимизации функций при помощи карт Карно:

1. Наносятся на карту все единичные значения полностью определенной функции, а если булева функция является частично определенной (недоопределенной, имеет безразличные состояния), то отмечаются и клетки, соответствующие наборам, на которых функция не определена.

2. Выполняются накрытия всех единичных (или всех нулевых) значений функции минимальным числом максимальных по площади правильных прямоугольников. Площадь прямоугольников подчиняется закону 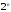, т.е. допустимое число клеток равно 1, 2, 4, 8 и т.д. Чем больше площадь накрытия, тем меньше переменных входит в результат, а чем меньше число накрытий, тем меньше конъюнкций будет в результате.

3. Записывается результат в виде логической суммы конъюнкций, составляющих каждое отдельное накрытие. Каждый член МДНФ (минимальная дизъюнктивная нормальная форма) составляется лишь из тех аргументов, которые для клеток соответствующей области имеют одинаковое значение (с инверсией либо без инверсии).

Для получения МКНФ функции замкнутыми областями охватываются клетки с нулевыми значениями функции, и при записи членов логического выражения берутся инверсии аргументов, на пересечении которых находятся области. Так, для функции, приведенной в таблице 2.4, МКНФ

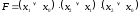(2.23)

Пример 2.1. Используя карты Карно, минимизировать функцию четырех переменных

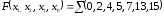. (2.24)

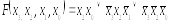
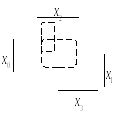
Рис. 2.4. Минимизация с помощью карты Карно функции (2.24)

Пример 2.2. Записать полученную в примере 2.1 МДНФ в базисах И–НЕ и ИЛИ–НЕ.

Для синтеза в базисе И–НЕ дважды инвертируем правую часть МДНФ

. (2.25)

Проводим преобразование по формуле Де Моргана:

(2.26)

Записываем выражение с использованием символа операции И–НЕ:

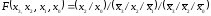. (2.27)

Выражению (2.27) соответствует схема, приведенная на рис. 2.5.

Рис. 2.5. Структурная схема функции, заданной выражением (2.27)

Для синтеза в базисе ИЛИ–НЕ запишем инверсную МДНФ функции (2.24) (рис. 2.6).

Дважды инвертируем каждую конъюнкцию и преобразуем их в инверсии дизъюнкций входных переменных с помощью правила Де Моргана

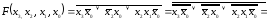
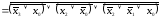. (2.28)

Записываем выражение (2.28) в базисе ИЛИ–НЕ

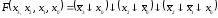. (2.29)

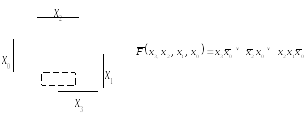
Рис. 2.6. Получение инверсной МДНФ функции (2.24)

Пример 2.3. С помощью карт Карно минимизировать не полностью определенную функцию, заданную таблицей истинности 2.5.

Таблица 2.5

	0	0	0	0	1	1	1	1
	0	0	1	1	0	0	1	1
	0	1	0	1	0	1	0	1
	*	0	1	*	1	*	*	1

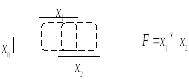
Рис. 2.7. Минимизация с помощью карты Карно не полностью определенной функции

Карты Вейча принципиально ничем не отличаются от карт Карно, кроме координатной сетки, которую образуют переменные, делящие карту несколько по иному. Синтез схем по этим картам выполняется по тому же алгоритму, что и для карт Карно.