5.4. Линейные сети

Линейные нейронные сети по своей структуре аналогичны персептрону и отличаются лишь функцией активации, которая является линейной. Выход линейной сети может принимать любое значение, в то время как выход персептрона ограничен значениями 0 или 1. Линейные сети способны решать только линейно отделимые задачи классификации. В них используется правило обучения, основанное на методе наименьших квадратов, настройка параметров выполняется таким образом, чтобы обеспечить минимум ошибки. Настройка линейной сети может быть выполнена с помощью как процедуры адаптации, так и процедуры обучения; в последнем случае используется правило обучения WH (Widrow – Hoff).

Адаптируемые линейные нейронные сети ADALINE (ADAptive Linear Neuron networks) позволяют корректировать веса и смещения при поступлении на вход каждого нового элемента обучающего множества. Такие сети широко применяются при решении задач обработки сигналов и в системах управления.

На рис. 4 показан линейный нейрон с двумя входами.

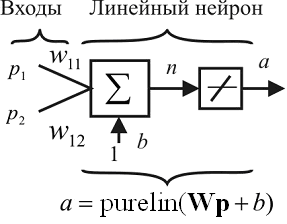
Рис. 4. Линейный нейрон

Выход сети определяется выражением

. (4)

Линейная сеть задает в пространстве входов разделяющую линию, на которой функция активации п равна 0 (рис. 5.).

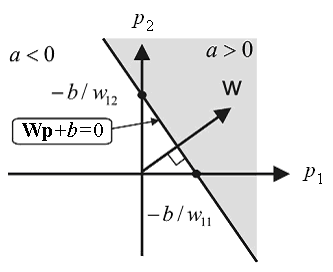
Рис.5. Линейно разделимое пространство входов

Векторы входа, расположенные выше этой линии, соответствуют положительным значениям выхода, а расположенные ниже – отрицательным. Это означает, что линейная сеть может быть применена для решения задач классификации. Однако такая классификация может быть выполнена только для класса линейно отделимых объектов.

Архитектура сети

Линейная сеть, показанная на рис. 6, а, включает S нейронов, размещенных в одном слое и связанных с R входами через матрицу весов W.

На рис. 6, б показана укрупненная структурная схема этой сети, вектор выхода а которой имеет размер 5x1.

Создание модели линейной сети

Линейную сеть с одним нейроном, показанную на рис. 4, с помощью процедур пакета Neural Network системы MATLAB можно создать следующим образом:

net = newlin([-1 1; -1 1], 1);

а

б

Рис. 6. Архитектура линейной сети

Первый входной аргумент задает диапазон изменения элементов вектора входа; второй аргумент указывает, что сеть имеет единственный выход. Начальные веса и смещение по умолчанию равны 0.

Присвоим весам и смещению следующие значения:

net.IW{1, 1} =[2 3]; net.b{1} =[-4];

Теперь можно промоделировать линейную сеть для следующего предъявленного вектора входа:

p = [5; 6];

а = sim(net, p)

Обучение линейной сети

Для заданной линейной сети и соответствующего множества векторов входа и целей можно вычислить вектор выхода сети и сформировать разность между вектором выхода и целевым вектором, которая определит некоторую погрешность. В процессе обучения сети требуется найти такие значения весов и смещений, чтобы сумма квадратов соответствующих погрешностей была минимальной

Применим процедуру обучения с учителем, которая использует обучающее множество вида:

{p₁ t₁}, {p₂ t₂}, ..., {p_Q t_Q}, (5)

где р₁, р₂, ..., р_Q – входы сети; t₁, t₂, ..., t_Q – соответствующие целевые выходы.

Требуется минимизировать следующую функцию средней квадратичной ошибки:

. (6)

Настройка линейной сети для заданного обучающего множества может быть выполнена посредством прямого расчета с использованием М-функции newlind.

Предположим, что заданы следующие векторы, принадлежащие обучающему множеству:

P = [1 -1.2]; Т = [0.5 1];

Построим линейную сеть и промоделируем ее:

net = newlind(Р,Т); Y = sim(net, P);

net.IW{l, l}

Выход сети соответствует целевому вектору.

Зададим следующий диапазон весов и смещений, рассчитаем критерий качества обучения и построим его линии уровня (рис. 7):

w_range = -l:0.1: 0; b_range = 0.5:0.1:1;

ES = errsurf(P,T, w_range, b_range, 'purelin');

contour(w_range, b_range, ES, 20)

hold on ; plot(-2.2727e-001,7.2727e-001, 'x' ) ; hold off

Рис. 7. Критерий качества обучения

На графике знаком х отмечены оптимальные значения веса и смещения для данной сети. Демонстрационный пример demolinl поясняет структуру линейной сети, построение поверхности ошибок и выбор оптимальных настроек.

Для линейной нейронной сети используется рекуррентное обучающее правило наименьших квадратов, которое является намного более мощным, чем обучающее правило персептрона. Правило наименьших квадратов, или правило обучения WH {Уидроу-Хоффа), минимизирует среднее значение суммы квадратов ошибок обучения.

Процесс обучения нейронной сети состоит в следующем. Предположим, что можно оценивать полную среднюю квадратичную погрешность, используя среднюю квадратичную погрешность на каждой итерации. Сформируем частную производную по весам и смещению от квадрата погрешности на k-й итерации:

(7)

Подставляя выражение для ошибки в форме

(8)

получим

(9)

Здесь р_j(k) – j-й элемент вектора входа на k-й итерации. Эти соотношения лежат в основе обучающего алгоритма WH.

(10)

Результат может быть обобщен на случай многих нейронов и представлен в следующей матричной форме:

(11)

Здесь ошибка и смещение– векторы и – параметр скорости обучения. При больших значениях обучение происходит быстро, однако при очень больших значениях может приводить к неустойчивости. Используя правило обученияWH и метод наискорейшего спуска, всегда можно обучить сеть так, чтобы ее погрешность была минимальной.

М-функция learnwh предназначена для настройки параметров линейной сети и реализует следующее обучающее правило:

(12)

где Lr – параметр скорости обучения. Максимальное значение параметра скорости обучения, которое гарантирует устойчивость процедуры настройки, вычисляется с помощью М-функции maxlinlr.

С помощью демонстрационной программы demolin7 можно исследовать устойчивость процедуры настройки в зависимости от параметра скорости обучения.

Для обучения линейной нейронной сети может быть применена типовая процедура обучения с помощью М-функции train. Эта функция для каждого вектора входа выполняет настройку весов и смещений, используя М-функцию learnp. В результате сеть будет настраиваться по сумме всех коррекций. Каждый пересчет для набора входных векторов называется эпохой. Затем процедура train моделирует настроенную сеть для имеющегося набора векторов, сравнивает результаты с набором целевых векторов и вычисляет среднеквадратичную ошибку. Как только значение ошибки становится меньше заданного или исчерпано предельное число эпох, обучение прекращается.

Обратимся к тому же примеру, который использовался при рассмотрении процедуры адаптации, и выполним процедуру обучения.

Р = [1-1.2];% Вектор входов

Т= [0.5, 1] ; % Вектор целей

maxlr = 0.40*maxlinlr(Р, 'bias');

net = newlin([-2,2],1,[0],raaxlr);

% Расчет функции критерия качества

w_range = -l:0.2:1; b_range = -l:0.2:1; % Диапазоны значений веса и смещения

ES = errsurf(P,T, w_range, b_range, 'purelin');

% Построение поверхности функции критерия качества,

surfс(w_range, b_range, ES)

На рис. 8, а построена поверхность функции критерия качества в пространстве параметров сети.

В процессе обучения траектория обучения будет перемещаться из начальной точки в точку минимума критерия качества. Выполним расчет и построим траекторию обучения линейной сети для заданных начальных значений веса и смещения.

х = zeros(1,50); у = zeros(1,50);

net.IW{l} = l; net.b{l} = -1; % Начальные значения весов и смещения

х{1) = net.IW{l}; у(1) = net.b{l};

net.trainParam.goal = 0.001; % Пороговое значение критерия качества

net. trainParam. epochs = 1; % Число эпох

for i = 2:50,

[net, tr] = train(net,P,T);

x(i) = net.lW{l>;

y(i) = net.b{l}; end

contour(w_range, b_range, ES, 20), hold on plot(x, y,’-*'), hold off,

а

б

Рис. 8. Обучение нейронной сети

На рис. 8, б символом * отмечены значения веса и смещения на каждом шаге обучения; видно, что примерно за 10 шагов при заданной точности (пороговое значение критерия качества) 0.001 получим w = -0.22893, b = 0.70519. Это согласуется с решением, полученным с использованием процедуры адаптации.