4) Поверхностный пробой

Заряд, локализованный на поверхности полупроводника в месте выхода p-n-перехода, может вызывать сильное изменение напряженности электрического поля внутри p-n-перехода в приповерхностном слое и его ширины. В этом случае более вероятным может оказаться пробой приповерхностной области p-n-перехода.

7. Туннельные диоды

Туннельные диоды были изобретены в 1958 году. Туннельные диоды изготавливаются из сильно легированных полупроводников, находящихся в вырожденном состоянии. Как известно, уровни Ферми в таких полупроводниках находятся внутри зон: в зоне проводимости в n-полупроводниках и в валентной зоне в p-полупроводниках.

Н а рисунке 1 показана энергетическая диаграмма туннельного диода в равновесном состоянии. Видно, что имеет место перекрытие зон: валентная зона p-области частично перекрывается зоной проводимости n-области.

На рисунке 2 приведены графики функций плотности состояний g_n(E) для электронов в зоне проводимости и g_р(E) для дырок в валентной зоне, а также функций распределения электронов B(E) (занятых состояний) в зоне проводимости и дырок p(E) в валентной зоне (свободных состояний) для равновесного состояния (когда внешнее напряжение не приложено). Из этого рисунка видно, что против занятых состояний одной области p-n-перехода находятся свободные состояния соседней области. 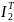Это делает возможным туннельное просачивание электронов из p- в n-область и из n-области в p-область: прямой и обратный туннельные токи. Прямой туннельный ток равен:

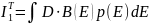, (1)

где D – величина, определяемая высотой (E) и шириной (d) барьера.

Обратный туннельный ток определяется другим соотношением:

. (2)

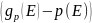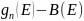В (2) функция – есть функция плотности занятых состояний электронов в валентной зоне, а функция ( ) – есть функция плотности свободных состояний электронов в зоне проводимости.

В равновесном состоянии интегралы (1) и (2) равны друг другу: = и результирующий ток равен нулю:

.

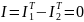При подаче на переход обратного смещения перекрытие зон увеличивается. При любом значении энергии занятых состояний p-области, лежащих против незанятых состояний n-области больше, чем занятых

состояний n-области, лежащих против незанятых состояний p-области. Поэтому интеграл (2) больше интеграла (1): 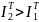и в переходе возникает ток (обратный(!)), который растет при увеличении обратного смещения.

П ри приложении к p-n-переходу прямого смещения степень перекрытия зон уменьшается, и занятых состояний n-области, лежащих против незанятых состояний р-области становится больше, чем занятых состояний р-области, лежащих против незанятых состояний n-области. Поэтому интеграл (1) больше интеграла (2): и в переходе возникает ток (прямой(!)), растущий при увеличении прямого смещения. Этот ток достигает максимального значения при совпадении максимумов ( ) функций распределения p(E) и B(E).

При дальнейшем росте прямого смещения число занятых состояний n-области, лежащих против свободных состояний p-области, уменьшается ввиду того, что часть занятых состояний лежит против запрещенной зоны (в запрещенную зону электроны переходить не могут), и ток уменьшается.

Прямой туннельный ток достигает нуля при таком смещении, при котором дно зоны проводимости n-области располагается на одной высоте с вершиной валентной зоны p-области (электронам некуда переходить!).

К ак и в обычном диоде увеличение прямого смещения вызывает инжекцию неосновных носителей заряда и появление в p-n-переходе диффузионного тока, растущего по экспоненте с ростом прямого смещения. Поэтому на вольт-амперной характеристике снова появляется ветвь тока, нарастающего с напряжением ( ).

Основной особенностью ВАХ туннельных диодов является наличие падающего участка, на котором диод обладает отрицательным (!) дифференциальным сопротивлением: 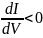. Это свойство позволяет использовать туннельные диоды для генерации электромагнитных колебаний, а также в качестве переключателей, смесителей и так далее. Так как в области туннельных токов накопление и рассасывание неосновных носителей практически отсутствует, то туннельные диоды обладают более совершенными частотными характеристиками и лучшим быстродействием по сравнению с обычными диодами и транзисторами.