Тема: Полупроводниковые диоды

1. Способы получения p-n перехода

Существует два способа получения p-n перехода: а) диффузионный и б) эпитаксиальный.

а) Диффузионный способ.

В этом случае р-n переход получают диффузией акцепторной примеси в полупроводник донорного типа (или наоборот). Диффузия проводится при высоких температурах, равных 1000 – 1300 ^оС, либо из твёрдого диффузанта, нанесённого на поверхность полупроводниковой пластинки, либо из газа, содержащего легирующую примесь, пропускаемого в виде потока над полупроводниковой пластинкой. В итоге получается следующее распределение примеси:

Такие p-n-переходы называются плавными.

б) Эпитаксиальный способ:

Эпитаксия – рост одного кристалла на поверхности другого. Эпитаксиальный способ – это осаждение на монокристаллическую подложку полупроводника n-типа монокристаллической плёнки полупроводника p-типа (или наоборот).

Такие p-n-переходы называются резкими.

2. Равновестное состояние p-n-перехода

Пусть ММ – плоскость раздела двух областей полупроводника (металлургический переход) с резким переходом. При 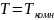примеси практически полностью ионизированы, так что концентрация основных носителей равна концентрации примесей: 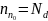, 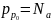(нижний индекс «нолик» обозначает равновесное состояние).

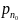П омимо основных носителей в полупроводниках содержатся еще и неосновные носители: дырки, с концентрацией в n-области и электроны с концентрацией 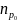в p-области.

Градиент концентрации однотипных носителей приводит к диффузионным потокам: электронов из n- в p-область и дырок из p- в n-область. При этом электроны, перешедшие из n-области, рекомбинируют с дырками, а дырки, перешедшие в n-область рекомбинируют с электронами. В результате в приконтактном слое как с той, так и с другой стороны образуется неподвижный объёмный заряд ионизированных примесей: доноров (в n-области) и акцепторов ((в р-области)).

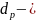Пусть и толщины слоёв объёмного заряда n- и p-областей, а общая толщина слоя объёмного заряда. Эти неподвижные объёмные заряды создают в p-n переходе контактное электрическое поле с разностью потенциалов . Это поле локализовано только в области перехода. Поэтому вне этого слоя, где нет объемных зарядов и нет поля, свободные заряды движутся так же хаотично, как и без контакта.

Если в слой объёмных зарядов влетает неосновной носитель, то контактное поле, которое для них является ускоряющим, подхватывает его и перебрасывает через этот слой. Часто при таком переходе он не успевает рекомбинировать. Наоборот, основные носители, для которых это поле замедляющее, могут перелететь через слой объёмных зарядов только в том случае, если их кинетическая энергия выше 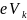. Поэтому образование объёмного заряда препятствует потоку основных носителей. Увеличение объёмного заряда вызывает уменьшение потока основных носителей. Такое увеличение объёмного заряда происходит до тех пор, пока поток основных носителей не сравняется с потоком неосновных носителей. При этом образуется состояние динамического равновесия. Таким образом, при равновесии через p-n переход текут равные между собой потоки электронов из n- в p-область и из p- в n-область, и равные между собой потоки дырок из p- в n-область и из n- в p-область.

Расчёты показывают, что если взять максвелловское распределение частиц по скоростям, то число носителей заряда, налетающих на слой объёмного заряда в единицу времени, равно

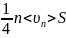, (2)

где n – концентрация, <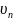 > – средняя скорость теплового движения, S – площадь поперечного сечения.

Согласно диодной теории контактное поле уменьшает потоки основных носителей, преодолевающих разность потенциалов , в 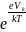раз, так что поток электронов из n- в p-область будет равен

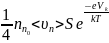. (3)

Этот поток равен потоку электронов из p- в n-область

. (4)

Откуда получаем:

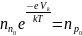. (5)

Из (5) следует, что

. (6)

Так как согласно закону действующих масс 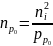, выражение (6) перепишется в виде:

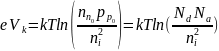. (7)

Приравнивание встречных потоков дырок даёт:

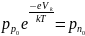(8)

и

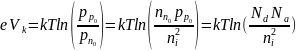. (9)

Из сравнения (7) и (9) следует, что (поскольку правые части (7) и (9) равны) встречные потоки как электронов, так и дырок выравниваются при одной и той же контактной разности потенциалов .

Из (6) и первой части уравнения (9) видно также, что тем больше, чем больше разница в концентрации носителей одного знака в разных областях. Отметим, кстати, что когда , что имеет место при высоких температурах, когда полупроводник переходит в область собственной проводимости, величина 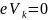и p-n-переход исчезает.

Установим теперь связь между величиной контактной разности потенциалов и разницей в энергиях уровней Ферми.

После установления равновесия для основных носителей образуется потенциальный барьер высотой , а уровни Ферми устанавливаются на одной высоте (!).

Для невырожденного полупроводника мы имеем:

в n-области:

, (10а)

а в p-области:

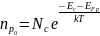, (10b)

где 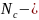эффективная плотность состояний у дна зоны проводимости. Подставив (10а) и (10b) в (6), получим:

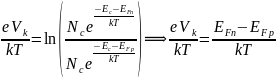. (11)

То есть

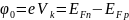. (12)

Если положить, что 1) донорные и акцепторные уровни ионизированы полностью, и 2) слой покинули все (!) электроны, а слой все (!) дырки и, кроме того, положить, что 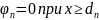и 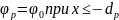, то расчёты, аналогичные проведённым для выпрямляющего контакта металл-полупроводник, дают:

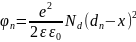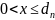при (со стороны n-полупроводника), (13)

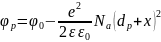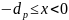при (со стороны p-полупроводника). (14)

Исходя из непрерывности функции при , получим, что . Откуда

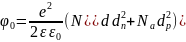. (15)

Исходя из свойств непрерывности первой производной при , получим:

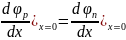. (15’)

Откуда:

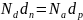(или ). (15’’)

Это означает, что в областях полупроводника, прилегающих к p-n переходу, объёмные заряды равны.

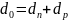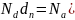Из условия и уравнения (15”) (которое можно переписать в двух видах ) и )) можно получить следующие соотношения:

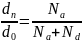; . (15’’’)

Используя эти условия, равенство (15) переписывается в виде:

. (15””)

Отсюда следует выражение для полной толщины слоя объёмного заряда p-n-перехода :

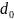. (16)

Согласно (16) толщина тем больше, чем меньше концентрация примесей (как 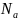, так и ). Из (15”) видно, что глубина проникновения контактного поля больше в той области, которая легирована слабее. Если , например, то согласно (15’”) практически весь слой локализуется в n-области, и в соответствии с (16):

. (17)

Проведённый расчёт относится к резкому p-n переходу. В случае плавного перехода, если считать, что изменение концентрации примеси происходит по линейному закону, из решения уравнения Пуассона получаем:

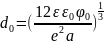, (18)

где 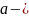коэффициент пропорциональности в уравнении:

. (19)