
- •Тема: Элементы зонной теории твёрдых тел
- •Уравнение Шредингера для электрона в кристалле
- •2.Функция Блоха
- •3. Метод Кронига-Пенни
- •4. Первая зона Бриллюэна
- •5. Дисперсионные кривые
- •6. Поступательное движение электронов в кристалле
- •7. Движение электрона в кристалле под действием внешней силы. Квазиимпульс электрона. Эффективная масса электрона
- •Тема: Неравновесные носители заряда в полупроводниках
- •1. Равновесные и неравновесные носители заряда (определение)
- •2. Время жизни. Скорости генерации и рекомбинации
- •3. Уравнение непрерывности
- •4. Диффузия и дрейф неравновесных носителей
- •4.1. Введение
- •4.2. Эффективный коэффициент диффузии
- •4 .3. Стационарное распределение неравновесных носителей за слоем генерации
- •4.4. Максвелловское время релаксации
- •Тема: Оптические явления в полупроводниках
- •Поглощение света полупроводниками
- •Коэффициент поглощения света
- •1.2. Собственное поглощение
- •1.3. Экситоны
- •1.4. Поглощение света свободными носителями зарядов
- •1.5. Переходы между подзонами
- •1.6. Примесное поглощение
- •Тема: Эффект Ганна
- •1. Возникновение отрицательной дифференциальной проводимости в полупроводниках в сильных электрических полях
- •2. Отрицательная дифференциальная проводимость в сильном электрическом поле в арсениде галлия
- •3. Электростатистические домены в полупроводниках
- •Тема: Контакт металла с полупроводником
- •Запирающий слой
- •Энергитические уровни в полупроводнике и металле
- •Выпрямление на запирающем контакте металла и полупроводника
- •Тема: Полупроводниковые диоды
- •Способы получения p-n перехода
- •Равновестное состояние p-n-перехода
- •3. Барьерная ёмкость p-n-перехода
- •4. Токи, протекающие через p-n-переход
- •5. Импульсные и высокочастотные свойства p-n-перехода
- •5.1. Импульсные свойства
- •5.2. Диффузионная емкость p-n-перехода
- •5.3. Способы повышения быстродействия диодов
- •5.4. Высокочастотные свойства p-n-перехода
- •6. Пробой p-n-перехода
- •1) Тепловой пробой
- •2) Лавинный пробой
- •3) Туннельный пробой
- •4) Поверхностный пробой
- •7. Туннельные диоды
- •8. Лавинно-пролетные диоды
- •Тема: Физические принципы работы транзисторов
- •1. Принцип работы биполярного транзистора
- •2. Параметры и выходные характеристики транзисторов
- •2.1. Параметры транзисторов
- •Выходные характеристики транзистора
- •2.3. Схема с общим эмиттером
- •Физическая природа усиления тока в схеме с общим эмиттером
- •2.4. Пробой коллекторного перехода
- •3. Переходные процессы в транзисторах. Дрейфовые транзисторы
- •3.1. Переходные процессы в транзисторах
- •3.2. Дрейфовые транзисторы
- •3.3. Предельная частота усиления
- •5. Полевые (униполярные) транзисторы
- •5.1. Полевые транзисторы мдп-структуры (с изолированным затвором)
- •5.1.1. Структура металл-диэлектрик-полупроводник
- •5.1.2. Полевые транзисторы мдп-структуры
- •5.2. Полевые транзисторы с управляющим p-n-переходом
Тема: Элементы зонной теории твёрдых тел
Уравнение Шредингера для электрона в кристалле
Уравнение Шредингера для электрона в кристалле имеет вид:
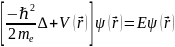 , (1)
, (1)
где
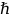 – постоянная Планка, деленная на 2,
me
– масса электрона,
– постоянная Планка, деленная на 2,
me
– масса электрона,
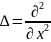 +
+
 – оператор Лапласа;
– оператор Лапласа;
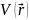 –
потенциальная энергия электрона,
–
потенциальная энергия электрона,
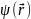 – волновая
функция и Е – полная энергия электрона.
– волновая
функция и Е – полная энергия электрона.
Потенциальная энергия электрона обладает трёхмерной периодичностью. Что это значит? В идеальном кристалле атомы расположены с идеальной периодичностью. Такое расположение атомов означает, что при смещении кристалла на вектор
 ,
(2)
,
(2)
(где
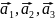 –
периоды идентичности решётки по трём
произвольным направлениям, а
–
периоды идентичности решётки по трём
произвольным направлениям, а
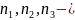 произвольные
числа) кристалл совмещается сам с собой.
Из этого следует, что точка с
радиусом-вектором
произвольные
числа) кристалл совмещается сам с собой.
Из этого следует, что точка с
радиусом-вектором
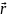 и точка с радиусом-вектором
+
и точка с радиусом-вектором
+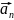 физически
эквивалентны и следовательно
физически
эквивалентны и следовательно
 .
(3)
.
(3)
Это соотношение как раз и выражает условие трёхмерной периодичности потенциального поля кристалла.
2.Функция Блоха
В
периодическом поле кристалла волновая
функция электрона
должна отличаться от волновой функции
электрона
 только постоянным множителем C:
только постоянным множителем C:
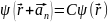 . (4)
. (4)
Из условия нормировки волновой функции следует, что
 (5)
(5)
Поэтому можно положить, что
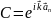 , (6)
, (6)
так
как
 .
Действительно
.
Действительно
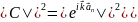 =
=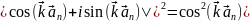 +
+ =1.
(7)
=1.
(7)
Здесь
 –
волновой вектор, модуль которого (|
|)
равен
–
волновой вектор, модуль которого (|
|)
равен
 .
.
Подставив (6) в (4), получим:
 (8)
(8)
Из (8) следует, что
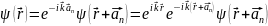 =
= (9)
(9)
где
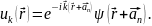 (10)
(10)
Нижний
индекс k
указывает на зависимость функции
 от k.
от k.
Функция
 обладает трёхмерной периодичностью
кристаллической решётки, то есть
обладает трёхмерной периодичностью
кристаллической решётки, то есть
 =
.
Действительно, согласно (10) и (8) мы имеем:
=
.
Действительно, согласно (10) и (8) мы имеем:
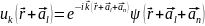 =
=
 =
= =
=
 (11)
(11)
Таким образом, стационарная волновая функция электрона в периодическом поле кристалла зависит от волнового вектора и имеет вид (см. формулу (9)):
 , (12)
, (12)
где
 – представляет собой плоскую
волну, бегущую в направлении
,
а
– некая функция координат, зависящая
от волнового вектора
и
имеющая периодичность
решётки.
Функция
электрона
– представляет собой плоскую
волну, бегущую в направлении
,
а
– некая функция координат, зависящая
от волнового вектора
и
имеющая периодичность
решётки.
Функция
электрона
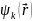 в виде (12) называется функцией
Блоха.
в виде (12) называется функцией
Блоха.
Если функцию Блоха подставить в стационарное уравнение Шредингера, то получим:
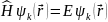 .
(13)
.
(13)
Из
(13) следует, что энергия электрона в
кристалле E
должна
зависеть
от волнового вектора
,
то есть
 .
.
Таким образом, можно констатировать:
Решением уравнения Шредингера для электрона в периодическом поле кристалла является бегущая плоская волна, модулированная с периодичностью кристалла, а энергия электрона зависит от волнового вектора.
3. Метод Кронига-Пенни
Некоторые
из характерных особенностей движения
электрона в кристалле можно
продемонстрировать на решении одномерной
задачи с гребенчатым
потенциалом Кронига-Пенни
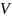 ,
изображенным на рис. 1.
,
изображенным на рис. 1.

Рис.1. Одномерный периодический потенциал Кронига-Пенни
Эта модель достаточно искусственна. Однако она хороша тем, что в ней весь расчёт производится точно и из нее следуют далеко идущие выводы.
В данном одномерном случае стационарное уравнение Шредингера для электрона имеет вид:
 (14)
(14)
Его решение будем искать в виде функции Блоха для одномерного случая:
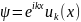 ,
(15)
,
(15)
где
 периодическая функция от
периодическая функция от
 с периодом
с периодом
 .
.
На
рис. 2. приведено решение уравнение
Шредингера (29) для энергии


Рис. 2. Зависимость E(k)
Как видно из этого рисунка (и это самое главное!), в зависимости E(k) имеются зоны разрешённых(!) и запрещённых(!) значений энергии.
